字符串匹配算法-KMP

字符串匹配问题

引用知乎用户灵茶山艾府的举例，假设我们有两个角色，甲和乙

甲:abbaabbaaba
乙:abbaaba

一天清晨，乙对甲说，你心里到底有没有我，告诉一下我在你心中的位置。甲心中一紧，从头开始一一与乙的字符进行比较。

但是，前面的六位都能匹配，当比较到第七位时，不匹配。甲试着像往常一样暴力匹配，回退到自己的第二个字符，从乙的开头开始继续比较。这一位匹配，则继续匹配下一位，不匹配再回退到上一次开始匹配的下一个字符重头开始匹配。如下图所示：

这样没过一会儿，甲就对乙说，我找到了，放心吧，我心里一直有你呢，然后骄傲地告诉了乙在自己心中的具体位置。乙表示还不错，一是觉得心里面有它，二是甲的查询速度这么快，说明甲没有其他相好的再心里(甲心里存放的字符数目较少). 但终有一天，甲心中想的相好的越来越多，而且这些相好的很大一部分还和乙很像，这样，甲的字符串就变得越来越长。

又是一个清晨，乙又对甲说，你心里到底还有没有我。甲JH一紧，捏了一把冷汗，心想自己心里现在不是那么干净，相好的那么多，要是还像以前那么暴力搜索，不知道要找到什么时候。果然，乙又开口了，快告诉我在你心中的位置。不过，乙又说，今天天气好，我先出去买几件化妆品，回来你必须告诉我，不然我们就…。甲心中暗自松了一口气，还好还好。待乙出门不久，甲赶紧翻出了尘封多年的数据结构与算法，它似乎记得当年学过那么一个kan_mao_pian算法可以解决自己的燃煤之急。

KMP算法

简介

KMP 算法是 D.E.Knuth、J,H,Morris 和 V.R.Pratt 三位神人共同提出的，称之为 Knuth-Morria-Pratt 算法，简称 KMP 算法。该算法相对于 Brute-Force（暴力）算法有比较大的改进。KMP算法的核心，在于构建一个部分匹配表next数组，利用之前判断过的信息，通过一个next数组，保存模式串中前后最长公共子序列的长度，每次回溯时，通过next数组找到前面匹配过的位置，省去了大量的计算时间。它不再像暴力匹配一样在不匹配的情况的要回退到原来位置下一位重新开始匹配。这里，部分匹配表数组是由前缀，后缀信息，通过计算前缀和后缀的最大。

前缀/后缀/部分匹配表

部分匹配值就是前缀和后缀拥有最长的共有元素的个数，以"ABCDABD"为例
A-前缀和后缀都是空集，最长的共有元素的个数为0.
AB-前缀为[A],后缀为B,最长的共有元素的个数为0.
ABC- 前缀为[A,AB],后缀为[BC,C],最长的共有元素的个数为0.
ABCD-前缀为[A,AB,ABC],后缀为[BCD,CD,D],最长的共有元素的个数为0.
ABCDA-前缀为[A,AB,ABC,ABCD],后缀为[BCDA,CDA,DA,A],最长的共有元素的个数为1.
ABCDAB-前缀为[A,AB,ABC,ABCD,ABCDA],后缀为[BCDAB,CDAB,DAB,AB,B],最长的共有元素AB的个数为2.
ABCDABD-前缀为[A,AB,ABC,ABCD,ABCDA,ABCDAB],后缀为[BCDABD,CDABD,DABD,ABD,BD,B],最长的共有元素的个数为0.

因此，"ABCDABD"的部分匹配表如下：

哦，原来部分匹配表next是这样生成的所，在乙回来前找到在自己心中的位置，甲心中有了几分把握。那部分匹配表的代码部分如何实现呢?甲忍不住继续往下看了看。

/**
	 * 模式串的部分匹配表生成
	 * @param pattern  模式串
	 * @return 部分匹配表
	 */
	public static int[] kmpNext(String pattern)
	{
		// 初始化部分匹配表
		int[] next = new int[pattern.length()];
		next[0] = 0;
		
		int k = 0;
		for(int j = 1;j<pattern.length();j++)
		{
			while(k> 0 && pattern.charAt(j) != pattern.charAt(k))
			{
				k = next[k-1]; // 此处最难理解，也是核心代码
			}
			
			if(pattern.charAt(j) == pattern.charAt(k))
			{
				k++;
				next[j] = k;
			}
		}
		return next;
	}

其他都还好理解，关于**k = next[k-1]**这段反人类的语句; 甲却是百思不得其解。

甲的疑问1：k = next[k-1]是什么鬼？

不虚不虚，甲不停安慰自己。然后他把next这个部分匹配表的求解过程分为三种情况，以模式串"abababzabababa"为例，分为以下三种情况：

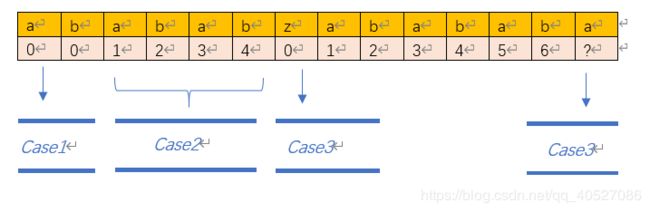
我们把字符数组记作pattern[], 将要构建的部分匹配表记作next[]，部分匹配表的构建过程其实就是pattern[]字符数组自己匹配自己的过程。

• Case-1: j=0的时候，此时字符串的前缀和后缀均为空集，最长的共有元素的个数自然为0。
• Case-2: pattern[k] == pattern[j]，如下图举个栗子：
  
  此时，k++，j++,并将next[j]赋值为k++后的k值，一直到红色标记的块之前，都符合case-2。
• Case-3: pattern[k] != pattern[i],置k = next[k-1]这里就是甲不得其解的地方。
  
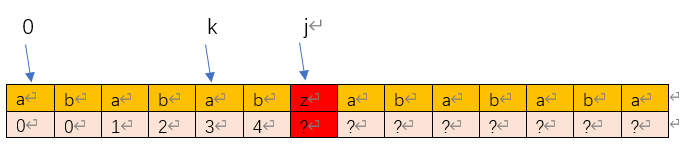
  此时，按照case-2一路匹配下来，k和i两个索引分别指向如上图所示。（此时next[j]到next[end]这部分的部分匹配表还没有生成,记作？)。好了，在这种情况下，我们置k = next[k-1]，到底是什么意思呢？

我们人工debug一下瞧一瞧，注意整个过程j指针不移动，直到遇到pattern[k] == pattern[i]

1)此时，k=4,然后置k=next[k-1]=next[3]=2.
2)k=2时，pattren[k]=a,pattern[j]=z,此时pattern[k] != pattern[i]，继续执行k=next[k-1]=next[1]=0.
3)k=0时，pattren[k]=a,pattern[j]=z,此时pattern[k] 仍然不等于 pattern[i]，不能发生匹配，此时再往下不可能会再有匹配，因此退出while循环，置next[j] = 0;

到这里，也许甲已经发现了一些可以解释的地方，它又继续往下走找下一个会出现case-3的匹配失败的情形再次研究。经过上面的debug后，k和j的指向如下：

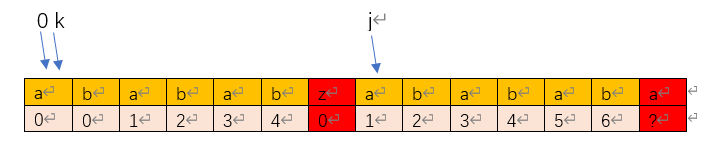
从这里，又开始出现case-2的情形，这种情况很好处理也很好理解，我们一直匹配到下一个会发生case3的情况如下。

此时，如果不算上最后一位pattern[j], pattern[0:k]和pattern[k+1:j]这两部分前后缀可以匹配，且最大长度为6，这些都好理解。但是再走一步我们就遇到不匹配了，好的，置k=next[k-1]对吧，甲又开始人工debug如下试图确认自己发现的规律。

1）k=6,置k=next[k-1]=next[5] = 4;
2) k=4,pattern[k]=a 和pattern[j]相等，发生匹配，k++,j++，并将k++后的置赋给next[j]。
next[j] = 5.
3) 我们假设pattern[j]即最后一位是x的情况，此时在k=4的情况下不发生匹配，我们还得找下一个k.
k = next[k-1]=k[3]=2, 仍然不匹配，继续置k= next[k-1]=k[1]=0，不发生匹配且由于k没有再回退的余地，计算next[j]的过程就结束了，next[j]=0.

甲思索良久，开始总结出以下规律。
k=next[k-1], 其实就是回退到模式串串上一次次大匹配的位置。
举个栗子，对子字符串 abababzababab 来说，前缀有 【a, ab, aba, abab, ababa, ababab, abababz, …】后缀有【 b, ab, bab, abab, babab, ababab, zababab, …】所以子字符串 abababzababab 前缀后缀最大匹配了 6 个（ababab），那次大匹配了多少呢，容易看出次大匹配了 4 个（abab），正好是next[k-1], 更仔细地观察可以发现，次大匹配的前缀后缀只可能在 ababab 中，所以次大匹配数就是 ababab 的最大匹配数！

在回到我们说的上面两个case-3栗子

• 第一个栗子
  abababz 当到达z时不再连续匹配，此时ababab的最大匹配为abab,长度为4.次大匹配为ab,长度为2，接着就没有更小的匹配了。而k通过置为next[k-1]也会依次从k=4->k=2->k=0.
• 第二个栗子
  abababzabababc 当到达c时不再连续匹配，此时abababzababab最大匹配为ababab,长度为6.次大匹配为abab,长度为4，次次大匹配为ab,长度为2，接着就没有更小的匹配了。而k通过置为next[k-1]也会依次从k=6- > k=4 -> k=2 -> k=0.

结论

甲恍然大悟，原来k=next[k-1]的目的是从次大匹配的长度开始进行下一次匹配。 如果从次大匹配的长度开始仍然不能匹配，则继续找次次大匹配…如果一直没有匹配到且模式串(字串)的指针已经到达了字符串串头，说明模式串前缀，后缀不会再有公共串，next[j]=0.

如果没能理解甲发现的规律，你也可以通过下面文章的不同角度来加深理解。
KMP算法—终于全部弄懂了

得到部分匹配表后匹配过程

以目标串：text，指针为 i ；模式串：pattern 指针为 j ; 为例

public static int kmpMatch(String text,String pattern,int[] next)
	{
		int j = 0;
		for(int i=0;i<text.length();i++)
		{
			while(j>0 && text.charAt(i) != pattern.charAt(j))
			{
				j = next[j-1];
			}
			if(text.charAt(i) == pattern.charAt(j))
			{
				j++;
			}
			if(j == pattern.length())
			{
				return i-j+1;
			}
		}
		return -1;
	}

哈哈，终于快速搜索到了乙在自己心中的位置，甲发现时间还早，这都多亏了KMP算法啊。

算法特点

1）匹配失败时，总是能够让 pattern 回退到某个位置，使 text 不用回退。
2）在字符串比较时，pattern 提供的信息越多，计算复杂度越低。