Codeforces Round #632 (Div. 2) C(计数题)(D 构造题) E(思维+构造) F(数学推导题)
题目链接
C. Eugene and an array
题意:给你n长度的序列,问你有多少个子序列(下标是连续的)是 好 的子序列
一个好的子序列定位:该序列中的子序列(下标不连续)没有和为0的。
做法:总的减去不合法的。
不合法的求法:l表示左边的边界。用前缀和得到当前左坐标 L 和 右坐标 R 区间内和为零。 左坐标的左边和右做坐标的右边都是可以组合一下 都是不合法的。
此时我们把边界l移到L+1 的位置 。因为如果下次 你又找到一个新的L1 R1 L<=L1的话 就会有重复计算的。
#include
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb push_back
#define pi pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
const int N=2e5+10;
ll n;
ll a[N],pre[N];
mapmp;
int main()
{
scanf("%lld",&n);
rep(i,1,n) scanf("%lld",&a[i]);
ll ans=n*(n+1)/2;
ll sum=0;
mp[0]=1;
int l=1;
rep(i,1,n)
{
pre[i]=pre[i-1]+a[i];
if(mp[pre[i]]>=l){
sum+=(n-i+1)*(mp[pre[i]]-l+1);
l=mp[pre[i]]+1;
}
mp[pre[i]]=i+1;
}
printf("%lld\n",ans-sum);
}
D. Challenges in school №41
读了半天发现还是读错了。
参考题意和题解链接:此
题解:
代码:
#include
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb push_back
#define pi pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
const int N=3e3+10;
char s[N];
vectorv[3000100];
int n,k,mink,maxk;
void print()
{
int p1=0,p2=0;
int kk=mink;
while(kk>n>>k>>s+1;
run(0);
while(v[mink].size()&&mink<=k)
{
maxk+=v[mink].size();
mink++;
run(mink);
}
//printf("mink:%d maxk:%d k:%d\n",mink,maxk,k);
if(mink<=k&&k<=maxk) print();
else puts("-1");
}
E. Road to 1600
题意有点难懂
题意和解法参考:博客
题意:
n*n的棋盘上有1~n^2 的数,且互不相同,一开始车和皇后都在数字为1的单元上(单独的一张棋盘上移动),且数字为1的这个单元被访问过了,车和皇后棋子 有以下移动规则:
1.当前棋子前往 所有可以移动但尚未被访问的单元中,数值最小的单元;
(每次只能走当前能到达的 且 之前 未到达的 格子中 数值最小的)
2.所有可移动的单元都被访问过了,则被传送到数值最少的未被访问的单元,执行该步需要1的花费;
3.所有单元格都要被访问。
要求找到n*n的棋盘,满足车的花费严格小于皇后的花费(不能都不花费),如果不存在则打印 -1
解法:大佬的解法真妙啊
#include
using namespace std;
const int N=5e2+10;
int a[N][N],n;
map >vis;
int main()
{
vis[1]=make_pair(3,2);
vis[2]=make_pair(4,4);
vis[3]=make_pair(1,2);
vis[4]=make_pair(1,1);
vis[5]=make_pair(2,2);
vis[6]=make_pair(1,3);
vis[7]=make_pair(2,1);
vis[8]=make_pair(4,2);
vis[9]=make_pair(2,3);
vis[10]=make_pair(3,4);
vis[11]=make_pair(3,3);
vis[12]=make_pair(1,4);
vis[13]=make_pair(4,1);
vis[14]=make_pair(3,1);
vis[15]=make_pair(2,4);
vis[16]=make_pair(4,3);
cin>>n;
if(n<=2){
puts("-1");
return 0;
}
if(n==3){
printf("%d %d %d\n",1,7,9);
printf("%d %d %d\n",3,2,5);
printf("%d %d %d\n",4,8,6);
return 0;
}
else if(n==4){
int now=0;
for(int i=1;i<=16;++i) a[vis[i].first][vis[i].second]=++now;
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j) printf("%d ",a[i][j]);
puts("");
}
return 0;
}
int now=0;
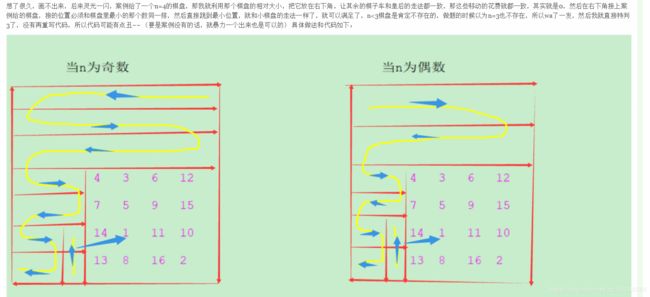
if(n%2==0){
for(int i=1;i<=n-4;++i){
int x=i,y;
if(i%2){y=1;while(y<=n) a[x][y++]=++now;}
else{y=n;while(y>=1) a[x][y--]=++now;}
}
}
else{
for(int i=1;i<=n-4;++i){
int x=i,y;
if(i%2){y=n;while(y>=1)a[x][y--]=++now;}
else{y=1;while(y<=n)a[x][y++]=++now;}
}
}
int x=n-3;
for(int i=1;i<=n-4;++i) a[x][i]=++now;
x=n-2;
for(int i=n-4;i>=1;--i) a[x][i]=++now;
x=n-1;
for(int i=1;i<=n-4-1;++i) a[x][i]=++now;
x=n;
for(int i=n-4-1;i>=1;--i) a[x][i]=++now;
a[n][n-4]=++now;
a[n-1][n-4]=++now;
int base=n-4;
for(int i=1;i<=16;++i) a[base+vis[i].first][base+vis[i].second]=++now;
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j) printf("%d ",a[i][j]);
puts("");
}
}
F. Kate and imperfection
题意:给你一个n 要你构造k长度的序列,序列从 1 到 n中取k个 。定义 这个序列中任意两个数的gcd的最大值为这个序列的等级。
现在要你求k 从2取到n 且每个序列的等级最小。
我的做法比较迷:2到n 每个数除以它的最小素因子排个序,输出这几个数就好了,推了几个样例得到的
有一个不错的解法:此
#include
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb push_back
#define pi pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
const int N=5e5+10;
int ans[N],v[N];
bool isPrime[N];
int prime[N];//保存素数
int num_prime;//记录素数个数
void init()
{
num_prime=0;
for(int i=2;i>n;
ans[1]=1;
for(int i=2;i<=n;++i) ans[i]=i/v[i];
sort(ans+1,ans+1+n);
for(int i=2;i<=n;++i) printf("%d ",ans[i]);
return 0;
}