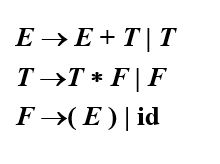【Python】代码实现LL(1),LR(1)上下文无关文法（Stack()类）

任务要求

针对书上第三章中的表达式文法，采用LL(1)、LR(1)进行分析

相关文法（需要进行消除左递归等操作）：

顺手分享一下课本资源好了（可能不是最新版，排版略有点别扭）
后文的书上内容就是指这本书：[编译原理].陈意云.文字版
提取码：e0ag

LL1介绍

LL(1):从左往右处理输入，最左推导，向前展望1个符号的，不带回溯的自上而下的算法，是上下文无关文法的子集。

LL1代码实现

书上P59-60

#LL1
import pandas as pd
class Stack:
    def __init__(self):
        self.values = "$E"
    
    def push(self, product):
        while product[-1:]!='→':
            if(product[-1:]=='\'' or product[-1:]=='d'):
                self.values+=product[-2:]
                product=product[0:-2]
            else:
                self.values+=product[-1:]
                product=product[0:-1]
                
    def pop(self):
        if(self.values[-1:]=='\''or self.values[-1:]=='d'):
            self.values=self.values[:-2];
        else:
            self.values=self.values[:-1]

    def top(self):
        if(self.values[-1:]=='\''or self.values[-1:]=='d'):
            return self.values[-2:]
        else:
            return self.values[-1:]
        
    def empty(self):
        return len(self.values) == 0
    
def Next_Char():#获取下一个词法记号
    global pend_input
    if(pend_input[0:2]=="id"):
         pend_input=pend_input[2:]
         return "id"
    else:
        t=pend_input[0:1]
        pend_input=pend_input[1:]
        return t

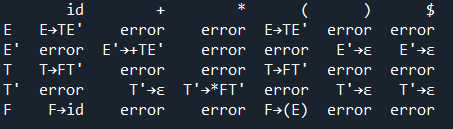
dic={#手工构造预测分析表
'id':['E→TE\'','error','T→FT\'','error','F→id'],
'+':['error','E\'→+TE\'','error','T\'→ε','error'],
'*':['error','error','error','T\'→*FT\'','error'],
'(':['E→TE\'','error','T→FT\'','error','F→(E)'],
')':['error','E\'→ε','error','T\'→ε','error'],
'$':['error','E\'→ε','error','T\'→ε','error']}
Analysis_table=pd.DataFrame(dic,index=['E','E\'','T','T\'','F'])

if __name__ == '__main__':
    stk = Stack()           #构造自定义栈
    #pend_input=input()+'$' #记得在输入内容后加上表示终止的"$"符号
    pend_input='id*id+id$'  #可手动输入亦可提前输入'待处理的输入内容'
    pend_head=Next_Char()   #取出第一个待处理的符号
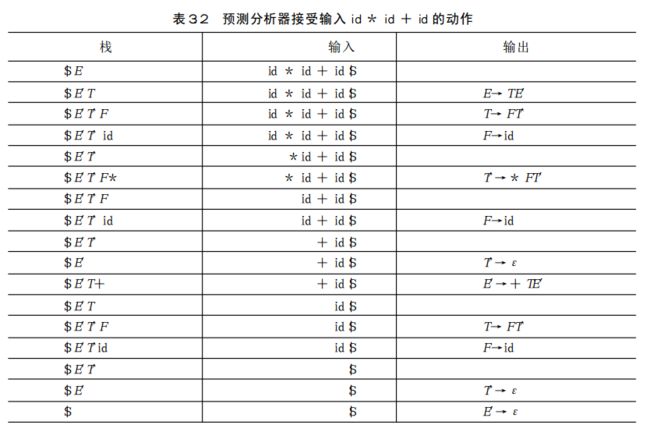
    print("预测分析器接受输入id*id+id的部分动作（与书上稍有不同）")
    print("%-15s"%"栈","%-15s"%"输入","%+10s"%"输出")
    while(stk.empty()==False):              
        if stk.top()==pend_head: 
            if pend_head!='$':
                print('----------------成功匹配符号:{}-------------------'.format(pend_head))
            pend_head=Next_Char()
            stk.pop()
        else:
            product=Analysis_table[pend_head][stk.top()]#获取产生式
            if product=='error':
                print('Error  Skip!')
                stk.pop()
            else:
                print("%-15s"%stk.values,"%-15s"%str(pend_head+pend_input),"%+15s"%product)
                stk.pop()
                if(product[-1:]!='ε'):#对于产生空串的产生式，只需弹栈，不需入栈
                    stk.push(product)

手动构造的预测分析表：

预测分析器接受输入id * id + id的相关动作：

LR1简略介绍

LR(1)：从左往右处理输入，构造一个最右推导的逆过程（规范规约），向前看1个符号的，自下而上的算法，是上下文无关文法的子集。

LR文法：我们能为之构造出所有条目都唯一的LR分析表。

LR分析器特点：适用于一大类上下文无关文法，效率高。

句型的句柄是和某产生式右部匹配的子串，并且，把它归约成该产生式左部的非终结符代表了最右推导过程的逆过程的一步。

活前缀：右句型的前缀，该前缀不超过最右句柄的右端。

LR1代码

书上P73-74

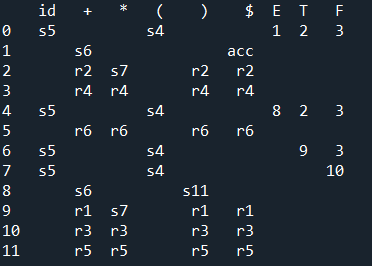
r后面的数字代表按第几个产生式做归约；s代表移进，它后面的数字转移到哪个状态。产生式：

#LR1
import pandas as pd
class Stack:
    def __init__(self):
        self.values = "0"
    def push(self, s):
        self.values=self.values+s
        def __init__(self):
            self.values = "0"             
    def pop(self):
        if(self.values[-2:]=='id'or self.values[-2:]=='10'or self.values[-2:]=='11'):
            self.values=self.values[:-2]
        else:
            self.values=self.values[:-1]
    def top(self):
        if(self.values[-2:]=='10'or self.values[-2:]=='id' or self.values[-2:]=='11'):
            return self.values[-2:]
        else:
            return self.values[-1:]
class Input_Token:
    def __init__(self):
        self.values = ""
    def Get_Token(self):#获取待处理字符串pend_input中下一个词法记号
        if(self.values[0:2]=="id"):
             self.values=self.values[2:]
             return "id"
        else:
            s=self.values[0:1]
            self.values=self.values[1:]
            return s
    def Show_Token(self):#查看待处理字符串pend_input的下一个词法记号（不取出）
        if (self.values[0:2] == "id"):
            return "id"
        else:
            s = self.values[0:1]
            return s

def Len_Right(p):
    p_char=p[p.find('→')+1:]
    if p_char=='id':
        return 1
    else:
        return len(p_char)

def LR1(head,top):#分析程序
    action=SLR[head][top]
    if action=='acc':#接受
        print("%-9s"%stk.values,"%+9s"%pend_input.values,"%+6s"%"接受")
        return False
    else:
        if action[0]=='s':#移进
            print("%-9s"%stk.values,"%+9s"%pend_input.values,"%+6s"%"移进")
            stk.push(pend_input.Get_Token())
            stk.push(action[1:])
        elif action[0]=='r':#归约
            production=Production[int(action[1:])]
            print("%-9s"%stk.values,"%+9s"%pend_input.values,"%+5s"%"按",production,"归约")
            for i in range(Len_Right(production)*2): #按照产生式右边长度的2倍出栈(1字符跟1数字)
                stk.pop()
            top_num=stk.top()
            left=production[0] #获取产生式左边的字符
            stk.push(left)
            stk.push(SLR[left][top_num])
        else:
            print('Error!\n Exit!')
            return False
        return True

dic={'id':['s5',' ',' ',' ','s5',' ','s5','s5',' ',' ',' ',' '],
      '+':[' ','s6','r2','r4',' ','r6',' ',' ','s6','r1','r3','r5'],
      '*':[' ',' ','s7','r4',' ','r6',' ',' ',' ','s7','r3','r5'],
      '(':['s4',' ',' ',' ','s4',' ','s4','s4',' ',' ',' ',' ',],
      ')':[' ',' ','r2','r4',' ','r6',' ',' ','s11','r1','r3','r5'],
      '$':[' ','acc','r2','r4',' ','r6',' ',' ',' ','r1','r3','r5'],
      'E':['1',' ',' ',' ','8',' ',' ',' ',' ',' ',' ',' '],
      'T':['2',' ',' ',' ','2',' ','9',' ',' ',' ',' ',' ',],
      'F':['3',' ',' ',' ','3',' ','3','10',' ',' ',' ',' ']}
SLR=pd.DataFrame(dic,index=['0','1','2','3','4','5','6','7','8','9','10','11'])#分析表
Production=['null','E→E+T','E→T','T→T*F','T→F','F→(E)','F→id']#产生式   
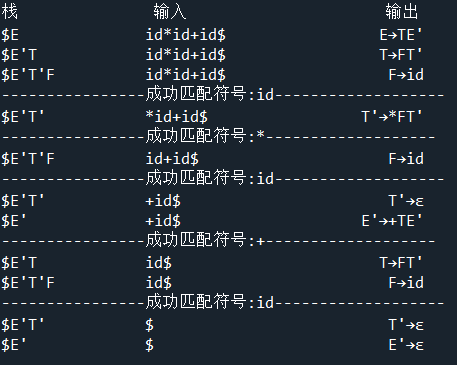
if __name__=='__main__':
    stk = Stack()
    pend_input=Input_Token()
    pend_input.values='id*id+id$'
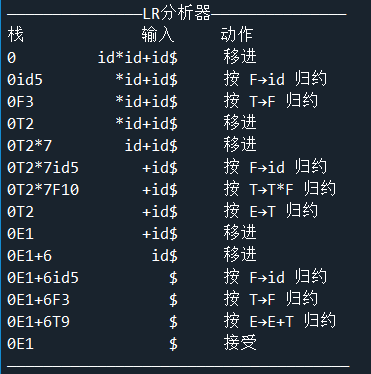
    print("———————————————LR分析器———————————————")
    print("%-7s"%"栈","%+8s"%"输入","%+6s"%"动作")
    while(True):
        if LR1(pend_input.Show_Token(),stk.top())==False:
            break
    print("——————————————————————————————————————")

分析表（action表）

实验结果：

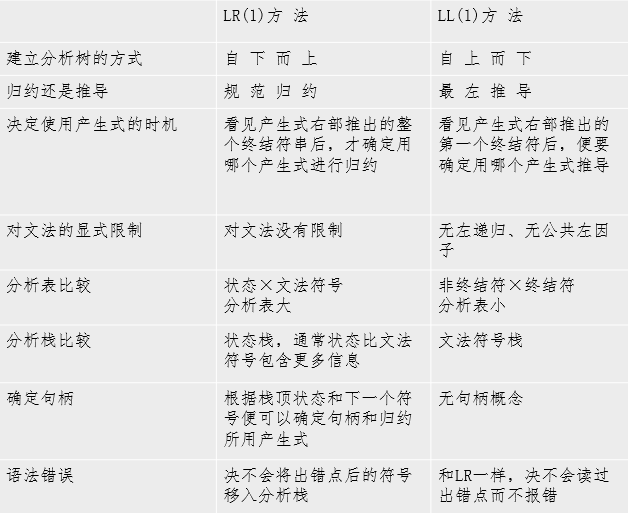
LR分析方法和LL分析方法的比较

部分参考资料

编译原理：语法分析2-非递归的预测分析

编译原理：语法分析3-LR分析器

编译原理:LL(1),LR(0),SLR(1),LALR(1),LR(1)对比

《编译原理》LR 分析法与构造 LR(1) 分析表的步骤 - 例题解析

Python栈实现