排序算法java实现——归并排序
归并排序
- 一、基本思路
- 二、算法分析
- 三、代码实现
一、基本思路
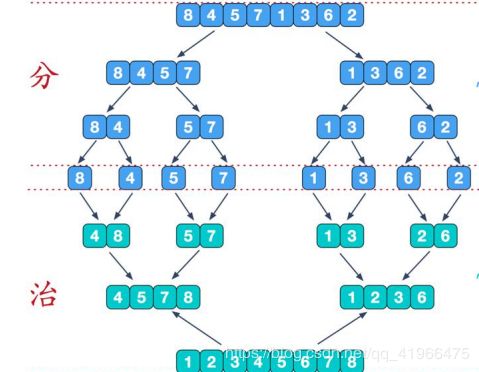
基本思路: 归并排序是利用归并的思想实现的排序方法,该算法采用经典的分治策略。先将待排序列分成若干个子序列,使每个子序列有序,再将已有序的子序列合并,得到完全有序的序列。
简单来说: 就是将待排序列分成几部分每部分分别排序,再进行合并。
举例:
有一序列为:8, 4, 5, 7, 1, 3, 6, 2要求按升序排列
- 先进行划分:(按照对半划分:下标mid = (left + right) / 2)
(1)(8,4,5,7),(1,3,6,2)
(2)(8,4),(5,7),(1,3),(6,2)
(3)(8),(4),(5),(7),(1),(3),(6),(2) - 再将有序子序列进行合并
(1)(4,8),(5,7),(1,3),(2,6)
(2)(4,5,7,8),(1,2,3,6)
(3)(1,2,3,4,5,6,7,8)
二、算法分析
时间: 归并排序需要递归的进行归并,根据递归树,f(n)=2*f(n/2)+O(n),自叶子向根节点构建,高度为 l o g 2 n {log_2{n}} log2n,每一层的总比较次数为n:可以得到时间复杂度为:O( n l o g 2 n n{log_2{n}} nlog2n)。
空间: 在归并排序中,我们用到了一个额外的临时空间来辅助排序,所以空间复杂度为:O(n),除此实现以外还有一种利用旋转操作的空间复杂度为O(1)的归并排序,这里不做详细说明。
| 算法 | 平均时间 | 最好情形 | 最差情形 | 稳定度 | 空间复杂度 | 备注 |
|---|---|---|---|---|---|---|
| 归并排序 | O(n l o g 2 n {log_2{n}} log2n) | O(n l o g 2 n {log_2{n}} log2n) | O(n l o g 2 n {log_2{n}} log2n) | 稳定 | O(n) | n大时较好 |
三、代码实现
package sort;
import java.util.Arrays;
/**
* @author dankejun
* @create 2020-04-29 15:40
*/
public class MergeSort {
public static void main(String[] args) {
int[] arr = {8, 4, 5, 7, 1, 3, 6, 2};
int[] temp = new int[arr.length];//辅助排序的临时数组
mergeSort(arr,0,arr.length-1,temp);
System.out.println(Arrays.toString(arr));
}
//递归实现
public static void mergeSort(int[] arr, int left, int right,int[] temp) {
if (left < right) {
int mid = (left + right) / 2;
mergeSort(arr,left,mid,temp);
mergeSort(arr,mid+1,right,temp);
merge(arr, left,mid,right,temp);
}
}
/**
* 合并
* @param arr 原始数组
* @param left 左边有序序列的初始索引
* @param mid 中间索引
* @param right 右边索引
*/
public static void merge(int[] arr, int left, int mid,int right,int[] temp) {
int i = left;//前半部分游标
int j = mid + 1;//后半部分游标
int t = 0;//临时数组索引
while (i <= mid && j <= right) {//前后两部分都还有元素未归并
if (arr[i] <= arr[j]) {//找到两部分中较小的元素按顺序放到临时数组中
temp[t] = arr[i];
t++;
i++;
} else {
temp[t] = arr[j];
t++;
j++;
}
}
while (i <= mid) {//前半部分还有元素未归并,后半部分元素都已经归并
temp[t] = arr[i];//将前半部分剩下的元素依次放到临时数组中
t++;
i++;
}
while (j <= right) {//后半部分还有元素未归并,前半部分元素都已经归并
temp[t] = arr[j];//将后半部分剩下的元素依次放到临时数组中
t++;
j++;
}
t = 0;//初始化临时数组游标
int tempLeft = left;
while (tempLeft <= right) {//将临时数组中归并好的元素放入到原数组中
arr[tempLeft] = temp[t];
t++;
tempLeft++;
}
}
}