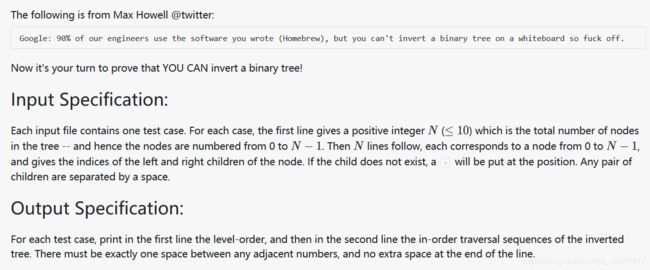
PAT A1102 Invert a Binary Tree

PAT A1102 Invert a Binary Tree

Sample Input:

8
1 -
- -
0 -
2 7
- -
- -
5 -
4 6

Sample Output:

3 7 2 6 4 0 5 1
6 5 7 4 3 2 0 1

word	meaning
Max Howell	马克斯·豪威尔
indices	(index的复数)

• 思路 1：使用静态二叉树（含父节点）

1. findRoot：从0节点开始，不断向上遍历到父节点为空（f == -1）
2. 从root开始，进行逆层序遍历，逆中序遍历（交换遍历左右子树的顺序即可）
3. 层序遍历，直接输出每次出队的元素，中序遍历是递归，不好控制输出，故用一个数组存储结果，遍历后再格式化输出

• code 1:

#include 
#include 
#include 
#include 
using namespace std;
const int maxn = 110;
int n, root;
char tmpl, tmpr;
struct Node{
	int data, lc, rc, f;
	Node(){
		f = lc = rc = -1;
	}
}node[maxn];
int findRoot(){
	int idex = 0;
	while(node[idex].f != -1){
		idex = node[idex].f;
	}
	return idex;
}
void revLevelOrder(int root){
	queue<int> q;
	q.push(root);
	int cnt = 0;
	while(!q.empty()){
		int now = q.front();
		cnt++;
		printf("%d", node[now].data);
		if(cnt != n) printf(" ");
		q.pop();
		if(node[now].rc != -1) q.push(node[now].rc); 
		if(node[now].lc != -1) q.push(node[now].lc);
	}
	printf("\n");
}
vector<int> in;
void revInOrder(int root){
	if(node[root].rc != -1) revInOrder(node[root].rc);
	in.push_back(root);
	if(node[root].lc != -1) revInOrder(node[root].lc);
}
void outputIn(){
	for(int i = 0; i < n; ++i){
		printf("%d", in[i]);
		if(i < n-1) printf(" ");
	}
}
int main(){
	scanf("%d", &n);
	for(int i = 0; i < n; ++i){
		getchar();	//!!!:Wrong 1: scanf读入char，要吸收掉上一轮结束时的\n 
		scanf("%c %c", &tmpl, &tmpr);
		if(tmpl == '-') node[i].lc = -1;
		else{
			node[tmpl-'0'].f = i;
			node[i].lc = tmpl - '0';
		} 
		if(tmpr == '-') node[i].rc = -1;
		else{
			node[tmpr-'0'].f = i;
			node[i].rc = tmpr - '0'; 
		}
		node[i].data = i;
	}
	root = findRoot();
	revLevelOrder(root);
	revInOrder(root);
	outputIn();
	return 0;
}

• 不需要output控制inOrder的输出：

vector<int> in;
int cnt1 = 0;
void revInOrder(int root){
	if(root == -1) return;
	if(node[root].rc != -1) revInOrder(node[root].rc);
	printf("%d", root);
	cnt1++;
	if(cnt1 < n) printf(" ");
	if(node[root].lc != -1) revInOrder(node[root].lc);
}

• TIPS: 遍历之前要判断结点是否为空

• 思路 2：
  在输入时，就交换左右孩子，然后按正常的层序遍历和中序遍历输出

• code 2:

#include 
#include 
#include 
#include 
using namespace std;
const int maxn = 110;
int n, root;
char tmpl, tmpr;
struct Node{
	int lc, rc;	//!!! TIPS 1:不需要data，下标就是idex 
}node[maxn];
bool has[maxn];	//找root 
int cnt = 0;
void print(int root){
//单独用一个print()控制输出格式 
	printf("%d", root);
	cnt++;
	if(cnt < n) printf(" ");
	else printf("\n");
}
int change(char c){
	return c == '-' ? -1 : c-'0'; 
}
int findRoot(){
	for(int i = 0; i < n; ++i){
		if(has[i] == false)
			return i;
	}
}
void levelOrder(int root){
	queue<int> q;
	q.push(root);
	while(!q.empty()){
		int now = q.front();
		print(now);
		q.pop();
		if(node[now].lc != -1) q.push(node[now].lc);
		if(node[now].rc != -1) q.push(node[now].rc); 
	}
	cnt = 0;
}
void inOrder(int root){
	if(root == -1) return;
	if(node[root].lc != -1) inOrder(node[root].lc);
	print(root);
	if(node[root].rc != -1) inOrder(node[root].rc); 
}
int main(){
	scanf("%d", &n);
	for(int i = 0; i < n; ++i){
		scanf("%*c%c %c", &tmpl, &tmpr);	//!!!:TIPS 2:"%*c"可以在scanf()中吸收一个字符 
		int lchild = change(tmpl), rchild = change(tmpr);
		//！！！输入时交换左右孩子 
		node[i].rc = lchild;
		if(lchild != -1) has[lchild] = true;
		node[i].lc = rchild; 
		if(rchild != -1) has[rchild] = true;
	}
 	root = findRoot();
	levelOrder(root);
	inOrder(root);
	return 0;
}

• TIPS 2: "%*c" 可以在scanf()中吸收一个字符

• 思路 3：
  先用后序遍历交换左右孩子，再层序和中序遍历

• code 3:

void postOrder(int root){
	if(root == -1) return;
	if(node[root].lc != -1) postOrder(node[root].lc);
	if(node[root].rc != -1) postOrder(node[root].rc);
	swap(node[root].lc, node[root].rc); 
}

• T2 code:

#include 
using namespace std;
const int maxn = 15;
struct Node{
	int lc, rc;
}node[maxn];
bool HasFather[256];
int FindRoot(int n){
	for(int i = 0; i < n; ++i){
		if(HasFather[i + '0'] == false) return i;
	}
}
//bool inq[maxn];
void RevLevel(int root, int n){
	int cnt = 0;
	queue<int> q;
	q.push(root);
//	inq[root] = true;	//层序遍历不需要inq[] 
	while(!q.empty()){
		int now = q.front();
		printf("%d", now);
		if(++cnt < n) printf(" ");
		q.pop();
		if(node[now].rc != -1) q.push(node[now].rc);
		if(node[now].lc != -1) q.push(node[now].lc);
	}
	printf("\n");
}
int cntIn = 0;
void RevIn(int root, int n){
	if(root == -1) return;
	RevIn(node[root].rc, n);	
	printf("%d", root);
	if(++cntIn < n) printf(" ");
	RevIn(node[root].lc, n);	
}

int main(){
	int n;
	scanf("%d", &n);
	for(int i = 0; i < n; ++i){
		char tl, tr;
		getchar();
		scanf("%c %c", &tl, &tr);
		node[i].lc = tl != '-' ? tl - '0' : -1;
		node[i].rc = tr != '-' ? tr - '0' : -1;
		HasFather[tl] = true;
		HasFather[tr] = true;
	}
	int root = FindRoot(n);
	RevLevel(root, n);
	RevIn(root, n);
	return 0;
}

• T3 code: 数组存储二叉树，先逆中序遍历，将中序序列存入一个vector，同时用id控制将节点存入一个数组，在遍历数组即得到逆层序序列

#include 
using namespace std;
const int maxn = 110;
int seq[maxn];
struct Node
{
    int data, lc, rc;
}node[maxn];
int Change(char s[])
{
    return s[0] == '-' ? -1 : atoi(s);
}
vector<int> in;
void RevInorder(int id, int root)
{
    if(root == -1) return;
    RevInorder(id * 2, node[root].rc);
    in.push_back(root);
    seq[id] = root;
    RevInorder(id * 2 + 1, node[root].lc);
}
int main()
{
    int n;
    scanf("%d", &n);
    int r = (n - 1) * n / 2 - (n + 1);
    for(int i = 0; i < n; ++i)
    {
        char lc[5], rc[5];
        scanf("%s %s", lc, rc);
        node[i].lc = Change(lc);
        node[i].rc = Change(rc);
        r -= (node[i].lc + node[i].rc);
    }
    memset(seq, -1, sizeof(seq));
    RevInorder(1, r);
    printf("%d", seq[1]);
    for(int i = 2; i < maxn; ++i)
    {
        if(seq[i] != -1) printf(" %d", seq[i]);
    }
    printf("\n");
    for(int i = 0; i < n; ++i)
    {
        printf("%d", in[i]);
        if(i < n-1) printf(" ");
    }
    return 0;
}