【20200408】数字图像处理DIP课程课业打卡五之图像的变换

叮嘟！这里是小啊呜的学习课程资料整理。好记性不如烂笔头，今天也是努力进步的一天。一起加油进阶吧！

一、DIP课程课业打卡五

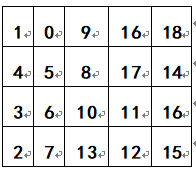
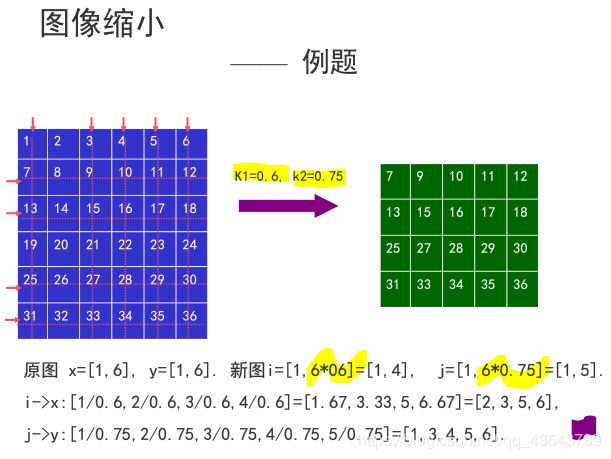
已知原始图像如图所示，基于像素采样的图像缩小方法对图进行缩小。设原图像大小为MN，将其缩小为k1Mk2N，（k1=0.5，k2=0.6）。

算法步骤如下：

1）设原图为F(x,y)，x=1,2,…,M；共M行  y=1,2,…,N. ；共N列。
  缩小后图像是G(i,j),  i=1,2,…,k1M；j=1,2,…,k2N。
2）新图的i行j列与原图的对应关系为：G(i,j)=F(i/k1, j/k1)。 

1、 请计算缩小后的新图像大小；

新图有___行，___列。

正确答案：2；3   

2、接上题。

请计算新图像的每一行对应原图像的哪一行；（计算结果四舍五入，取整数）

新图第1行对应原图___行；

新图第2行对应原图___行；

正确答案：2；4   

3、接上题。计算新图像的每一列对应原图像的哪一列；（计算结果四舍五入，取整数）

新图第1列对应原图___列；

新图第2列对应原图___列；

新图第3列对应原图___列；

正确答案：2；3；5

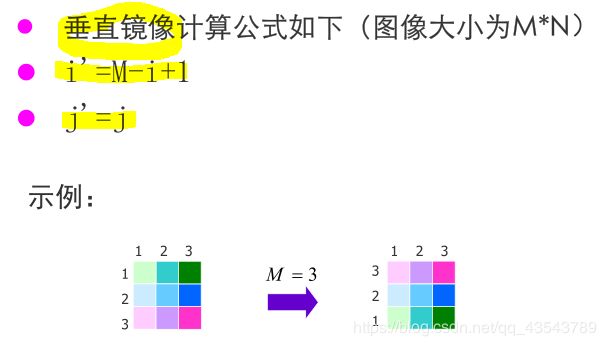
4、已知原图像F(i,j)，图像大小为M*N。
原图像F(i,j)到新图像G(i’, j’)的变换关系为：

i’=M-i+1
j’=j

则原图像到新图像的变换为___。

正确答案：
垂直镜像；镜像；图像垂直镜像；图像镜像

二、知识巩固

1、图像的几何变换

图像的几何变换包括了图像的形状变换和图像的位置变换。

 图像的几何变换不改变像素的值，只改变像素的位置。

 图像的形状变换 是指图像的放大、缩小与错切。
 图像的位置变换 是指图像的平移、镜像与旋转。
 图像的仿射变换 是采用通用的数学影射变换公式，来表示几何变换。

2、图像的位置变换

所谓图像的位置变换是指图像的大小和形状不发生变化，只是将图像进行 平移 、 镜像 和 旋转。

应用：图像的位置变换主要是用于目标识别中的目标配准。
（1）平移

实例：

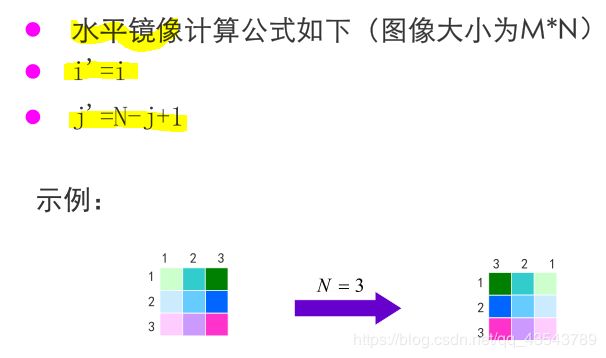
（2）镜像
所谓的镜像，通俗地讲，是指在镜子中所成的像。其特点是左右颠倒或者是上下颠倒。

镜像分为 水平镜像 和 垂直镜像。

（3）旋转

3、图像的形状变换

图像的形状变换主要是指图像的 缩小 、 放大与错切。

应用：图像的形状变换通常在目标物识别中使用。

（1）图像的缩小
分为按比例缩小和不按比例缩小两种。
 图像缩小之后，因为承载的信息量小了，所以画布可相应缩小。

图像缩小
—— 方法1：基于像素采样的图像缩小方法
—— 方法2：基于局部均值的图像缩小方法

（2）图像放大
图像放大从字面上看，是图像缩小的逆操作，但是，从信息处理的角度来看，则难易程度完全不一样。

图像缩小是从多个信息中选出所需要的信息，而图像放大则是需要对多出的空位填入适当的值，是信息的估计。

图像放大
—— 方法1：基于像素填充的图像放大方法
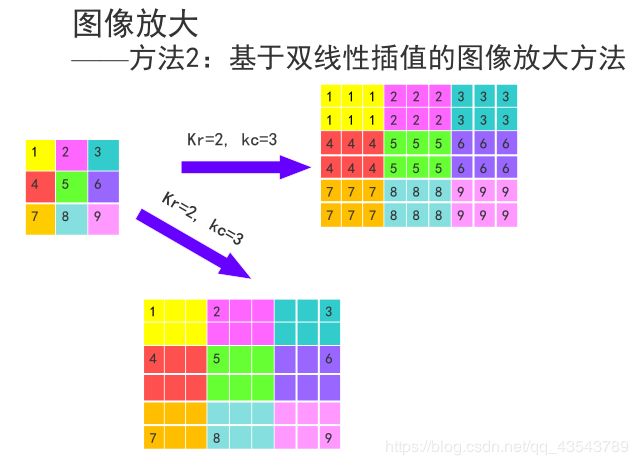
—— 方法2：基于双线性插值的图像放大方法

4、图像的形状变换之图像缩小

图像缩小实际上就是对原有的多个数据进行挑选或处理，
获得期望缩小尺寸的数据，并且尽量保持原有的特征不丢失。

（1）方法1：基于像素采样的图像缩小方法

最简单的方法就是等间隔地选取数据。

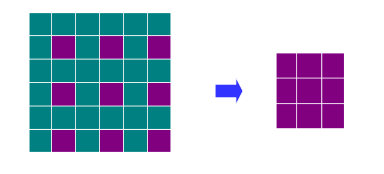
实现方法：
设原图像大小为M*N，缩小为 k1 M *k2 N，（k 1 <1，k 2 <1）。算法步骤如下：
1）设原图为F(x,y)，x=1,2,…,M, y=1,2,…,N.
压缩后图像是G(i,j), i=1,2,…,k1 M, j=1,2,…,k2 N.
2）G(i,j)=F(c 1 *i,c 2 *j)。
其中，c1 =1/k1 ； c2 =1/k2 。


图像缩小方法1伪代码

输入参数：图像矩阵F，行缩小比例k1，列缩小比例k2
输出参数：缩小后的矩阵G
处理：
1、得到原始图像尺寸M、N、d
2、得到新图像尺寸：M2、N2
3、初始化新图像矩阵G
4、对新图像的每一行for i=1:M2
5、对新图像的每一列for j=1:N2
6、计算新图像的i行j列对应原图像的坐标x、y
7、检查x、y的边界条件
8、将原图x、y点的灰度值赋给新图i、j点

（2）方法2：基于局部均值的图像缩小方法

图像缩小方法2伪代码

输入参数：图像矩阵I，行缩小比例k1，列缩小比例k2
输出参数：缩小后的矩阵G
处理：
1、得到原始图像尺寸M、N、d
2、得到新图像尺寸：M2、N2
3、初始化新图像矩阵G
4、对新图像的每一行for i=1:M2
5、对新图像的每一列for j=1:N2
6、计算新图像的i行j列对应原图中的图像块F，计算图像块F的行起止坐标x1、x2；列起止坐标y1、y2
7、检查x2、y2的边界条件
8、取得图像块F的灰度值（或者R、G、B颜色值），赋给新图的i、j点

5、图像的形状变换之图像放大

图像放大是需要对多出的空位填入适当的值，是信息的估计。

（1）方法1：基于像素填充的图像放大方法

最简单的思想是，如果需要将原图像放大为k倍，则将原图像中的每个像素值，填在新图像中对应的k*k大小的子块中。

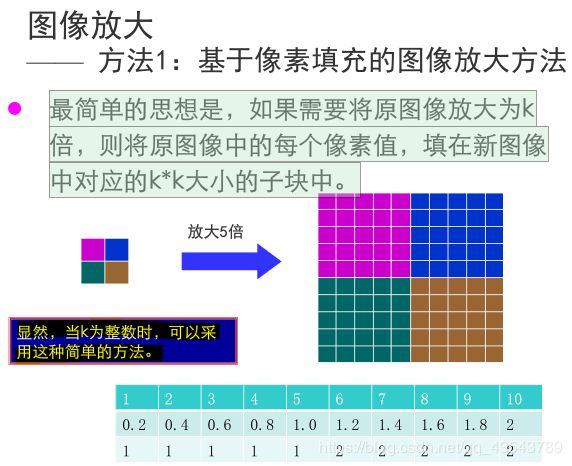
实现方法：

实例：

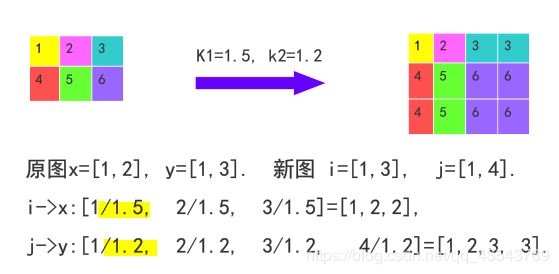
**按照前面这种方法处理，如果放大倍数太大，会出现马赛克效应**。

（2） 方法2：基于双线性插值的图像放大方法

伪代码实现：

输入参数：im,Kr,Kc：图像矩阵im，行放大比例Kr，列放大比例Kc
输出参数：放大后的图像矩阵im2

处理：
1、得到原始图像尺寸rowNum1,colNum1,D
2、得到新图像尺寸：rowNum2、colNum2
3、初始化新图像矩阵im2、顶点行号数组rowIndex、顶点列号数组colIndex
4、对原图像的每一行i【for i=1:rowNum1-1 】
  4.1：计算i行在新图像中对应顶点为第x行，记录顶点行号【rowIndex(i)= x】
  4.2：对原图像的每一列j【for j=1:colNum1-1】
     计算j列在新图像中对应顶点为第y列。将原图像的像素值赋给新图像对应 
     图像块的左上角【im2(x,y,:)=im(i,j,:)】并记录顶点列号【colIndex(j)= y;】
  4.3：对最后一列【 j= colNum1】
     计算j列在新图像中对应顶点为第y列。将原图像的像素值赋给新图像对应
     图像块的右上角【im2(x,y,:)=im(i,j,:)】并记录顶点列号【colIndex(j)= y;】
5、对最后一行【i = rowNum1;】
  5.1：for j=1:colNum1-1 将原图像的像素值赋给新图像对应图像块的左下角
  5.2：对j= colNum1，将原图像的像素值赋给新图像对应图像块的右下角
6、顶点行插值【 for i=1:rowNum1-1 】
  6.1初始化起始行和结束行的行号【 startPoint = rowIndex(i);
endPoint = rowIndex(i+1); 】
  6.2 对起始行和结束行之间的每一行t【for t= startPoint+1:endPoint-1】：
    6.2.1 求出起始行的所有像素值value1【value1 = im2(startPoint,:,:);】
    6.2.2 求出结束行的所有像素值value2【value2 = im2(endPoint,:,:);】
    6.2.3 根据value1、value2、 t、startPoint、endPoint的值，带入公式，计算得到新图像第t行的像素值valuex【im2(t,:,:)=valuex】
7、列插值 【for i=1:colNum1-1】
  7.1初始化起始列和结束列的列号【 startPoint = colIndex(i);
endPoint = colIndex(i+1); 】
  7.2 对起始列和结束列之间的每一列t【for t= startPoint+1:endPoint-1】：
    7.2.1 求出起始列的所有像素值value1【value1 =im2(:,startPoint,:);】
    7.2.2 求出结束列的所有像素值value2【value2 = im2(:,endPoint,:);】
    7.2.3 根据value1、value2、 t、startPoint、endPoint的值，带入公式，计算得到新图像第t列的像素值valuex【im2(:,t,:)=valuex】

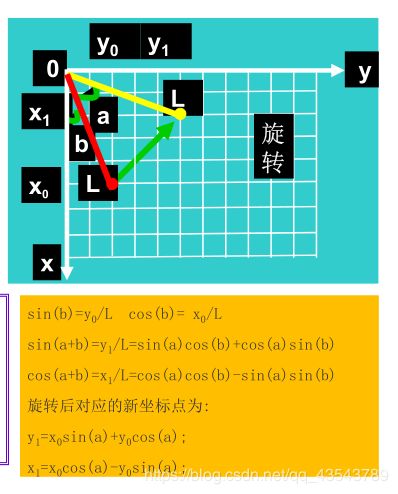
6、图像的位置变换之图像旋转

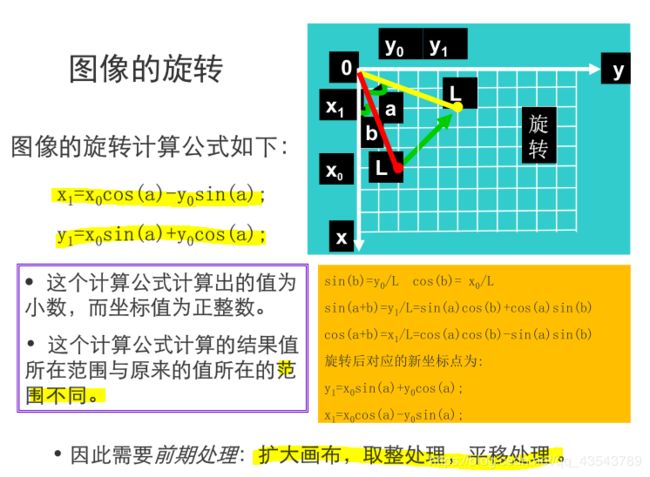
图像的旋转计算公式如下：
y1 =x0 sin(a)+y0 cos(a);
x1 =x0 cos(a)-y0 sin(a);

• 这个计算公式计算出的值为小数，而坐标值为正整数。
• 这个计算公式计算的结果值所在范围与原来的值所在的范围不同。
• 因此需要 前期处理 ：扩大画布，取整处理，平移处理 。

【01】图像旋转的前期处理—— 画布的扩大

 图像旋转之前，为了避免信息的丢失，画布的扩大是最重要的。
 画布扩大的原则是：以最小的面积承载全部的画面信息。

【02】图像旋转

 按照确定画布时的平移量取整。

图像旋转方法0伪代码实现：

输入参数：图像矩阵F，旋转角度a
输出参数：旋转后的图像矩阵G

处理：
1、获得图像尺寸，计算图像的四个顶点坐标。
2、根据旋转公式：x_2 = round(x*cos(a)-y*sin(a));
              y_2 = round(x*sin(a)+y*cos(a))，计算图像的四个顶点旋转后的坐标。
              （x、y为原始图像的坐标，x_2、y_2为对应点旋转后的坐标）
3、根据四个顶点旋转后的坐标，计算画布扩展后的大小M2、N2，并计算x和y方向的偏移量。初始化新图新G.
4、对原图像F的每一行for i=1:M
5、对原图像F的每一列for j=1:N
  5.1 根据旋转公式和x、y方向的偏移量，计算像素点F(i,j,:)旋转后在新图像G中的坐标x、y。
  5.2 将F(i,j,:)赋值给G(x,y,:)

【03】图像旋转后处理

旋转后的隐含问题分析

图像旋转之后，出现了两个问题：
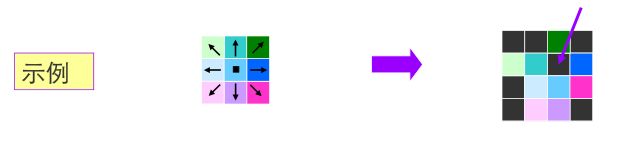
1）像素的排列不是完全按照原有的相邻关系。这是因为相邻像素之间只能有8个方向（相邻为45度），如下图所示。
2）会出现许多的空洞点。

解决问题的思路：

 出现问题的核心是像素之间的连接是不连续的。
 相邻像素的角度是无法改变的，所以只能通过增加分辨率的方法来从整体上解决这个问题。
 采用某种填补方法来填充空洞。

【处理方法】 图像旋转的后处理—— 插值

图像旋转方法1（插值法）伪代码

输入参数：图像矩阵F，旋转角度a
输出参数：旋转后的图像矩阵im

处理：
1、获得图像尺寸【[M,N,K] = size(I)】，计算图像的四个顶点坐标。
2、根据旋转公式：x_2 = round(x*cos(a)-y*sin(a));
              y_2 = round(x*sin(a)+y*cos(a))，计算图像的四个顶点旋转后的坐标。
              （x、y为原始图像的坐标，x_2、y_2为对应点旋转后的坐标）
3、根据四个顶点旋转后的坐标，计算画布扩展后的大小M2、N2，并计算x和y方向的偏移量。
4、初始化新图新G 【G= ones(M_2,N_2,K)*-1】
5、对原图像F的每一行for i=1:M
6、对原图像F的每一列for j=1:N
  6.1 根据旋转公式和x、y方向的偏移量，计算像素点F(i,j,:)旋转后在新图像G中的坐标x、y。
  6.2 将F(i,j,:)赋值给G(x,y,:)
7、使用近邻插值法进行空穴填充。对新图像的每一行【for i=1:M_2】
  7.1 找出新图像G第i行的所有非背景点的行列坐标
  7.2 求第i行所有非背景点的列坐标起止值ymin、 ymax
  7.3 对ymin、 ymax之间的每一个像素点，【for j=ymin+1:ymax】若该像素点为背景点 【 if(G(i,j,1)<0 】，则将前一个点的像素值赋给该点【 G(i,j,:)=G (i,j-1,:); 】 。

7、图像的旋转——反变换

反变换方法就是从新图形的像素坐标反过来计算对应原图像坐标点的坐标。

反变换法 伪代码实现：

输入参数：图像矩阵F，旋转角度a
输出参数：旋转后的图像矩阵G

处理：
1、获得图像尺寸，计算图像的四个顶点坐标。
2、根据旋转公式：x_2 = round(x*cos(a)-y*sin(a));
              y_2 = round(x*sin(a)+y*cos(a))，计算图像的四个顶点旋转后的坐标。（x、y为原始图像的坐标，x_2、y_2为对应点旋转后的坐标）
3、根据四个顶点旋转后的坐标，计算画布扩展后的大小M2、N2，并计算x和y方向的偏移量。初始化新图像G
4、对新图像G的每一行for i=1:M_2
5、对新图像G的每一列for j=1:N_2
  5.1 根据旋转反变换公式和x、y方向的偏移量，计算新图像的像素点G(i,j,:)旋转前在原图像F中对应的坐标x、y。
  5.2 如果(x>0 && x<=M && y>0 && y<=N)，则将F(x,y,:)的像素值采样并且赋给G(i,j,:)。

Ending！
更多课程知识学习记录随后再来吧！

就酱，嘎啦！

注：
人生在勤，不索何获。