CSP M4

目录

T1-TT数鸭子

题目分析：

代码：

T2-ZJM要抵御宇宙射线

题目分析：

代码：

T4-宇宙狗的危机

题目分析：

代码：

---

T1-TT数鸭子

题目分析：

该题关键在于求映射成的数的数位中不同的数字个数，因为ai的范围到达了e15，远远超出了int的范围，且时空范围也比较的严格，所以采用字符的形式的读入数，然后分别遍历字符串，找出0-9每个字符出现的次数，只要0-9中有不超过k个出现，那么就满足题意，ans++，最终输出结果ans即可。

（emmm，本来在测试时是过了的，但是后面补题的时候又TLE了。。。。然后把cin改成scanf又过了。。）

代码：

#include
#include
#include 
using namespace std;
int cnt[15];//0-9每一位出现的次数 
int main()
{
	int n,k;
	//cin>>n>>k;
	scanf("%d%d",&n,&k); 
	//string a;
	char a[20];
	int ans=0;
	for(int i=0;i>a;
		scanf("%s",a);
		memset(cnt,0,sizeof(cnt));
		int tol=0; 
		int len=strlen(a);
		for(int j=0;j

T2-ZJM要抵御宇宙射线

 

题目分析：

该题因为要找最小面积的保护罩，而且中心要为发射点。因为保护罩是圆形的，且保护罩应该要覆盖所有的发射点，所以以每个发射点为圆心的圆的半径要取该发射点到其他发射点的最大值，遍历所有发射点，找到每个发射点的半径，然后再进一步找到所有半径的最小值。

(emmm.....，这道题也不难，测试的时候也写的差不多了。。但是卡在第五个测试点了。。持续wronganswer on test5之后终于发现了问题在inf的赋值上，因为经过了平方操作，需要inf的赋值要大于e10）

代码：

#include
#include
#include 
#include
using namespace std;
const int maxn=1e3+5;
//#define inf 0x3f3f3f3f
double inf=1e15;
double minn=inf;
struct point
{
	double x;
	double y;
}vertex[maxn];

bool cmp(point u,point v)
{
	if(u.x!=v.x)
	{
		return u.x>n;
	for(int i=0;i>vertex[i].x>>vertex[i].y;
	}
	sort(vertex,vertex+n,cmp);
	double ansx=0;double ansy=0;
	double r=0;
	for(int i=0;i

T4-宇宙狗的危机

 

 

题目分析：

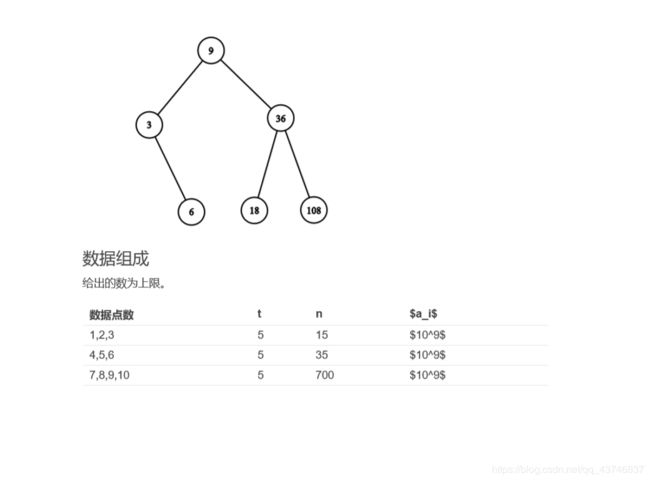
首先因为是二叉搜索树BTS，二叉搜索树的特点是要么是空树，要么要满足任意节点的左节点要小于该节点，右节点要大于该节点（左小右大），其中序遍历的结果是从小到大的。

这道题要用到dp动态规划思想，而且应该是区间DP。。

dp[i][j]表示以i，j为根节点的两子树可以相连。

L[i][j]表示以i为根节点的左子树，节点范围到j，同理R[i][j]表示以i为根节点的右子树，节点范围到j。

对于升序序列，进行区间遍历，三重循环，第一层为区间长度，第二层为左端点，第三层为区间内各点。如果(L[l][k]&&R[k][r])，那么说明左右两子树可以相连 ，相连之后的根节点为k，则dp[l][r]=1。因为要满足题意gcd超过1的要求，所以需要添加vis数组，vis[i][j]表示以i为根节点的子树和以j为根节点的子树的gcd是否超过1，如果超过1，vis=1，否则vis=0。在循环遍历中需要根据vis数组更新R[l-1][r]以及L[l][r+1]。最终判断dp[1[n]是否=1即可，如果dp[1][n]=1，那么说明1-n之间都可以相连，即能构成满足题意的二叉搜索树。

（emmm，测试的时候完全没有想到DP，建图建了好久。。。另外，这道题似乎卡时间卡的挺严格的，递归一直报TLE。。。gcd直接判定不用vis数组也报TLE。。。）
  

代码：

#include
#include
#include 
using namespace std;
const int maxn=705;

int dp[maxn][maxn];//表示l-r是否构成BST 0表示l-1，1表示r+1 
int vis[maxn][maxn];
int L[maxn][maxn],R[maxn][maxn];//L表示i为根左子树 R表示i为根右子树 
int a[maxn];

int gcd(int a,int b)//gcd最大公约数 
{
	return b==0?a:gcd(b,a%b);
}

int main()
{
	int t;
	cin>>t;
	int n;
	while(t--)
	{
		cin>>n;
		bool flag=false;
		memset(L,0,sizeof(L));
		memset(R,0,sizeof(R));
		
		for(int i=1;i<=n;i++)
		{
			cin>>a[i];
			L[i][i]=R[i][i]=1;
		}
		memset(dp,0,sizeof(dp)); 
		for(int i=1;i<=n;i++)
		{
			for(int j=i+1;j<=n;j++)
			{
				if(gcd(a[i],a[j])>1)//gcd>1 可以相连 
				{
					vis[i][j]=vis[j][i]=1;
				}
				else if(gcd(a[i],a[j])==1)//gcd=1 不可以相连
				{
					vis[i][j]=vis[j][i]=0;
				}	
			}
		}
		for(int len=1;len<=n;len++)//区间长度 
		{
			for(int l=1;l<=n-len+1;l++)//区间左端点 
			{
				int r=l+len-1;//区间右端点 
				for(int k=l;k<=r;k++)
				{
					if(L[l][k]&&R[k][r])//左右两子树可以相连 
					{
						dp[l][r]=1;
						if(vis[l-1][k]) 
						{
							R[l-1][r]=1;
						}
						if(vis[k][r+1])
						{
							L[l][r+1]=1;
						}	 
					}	
				}
			}
		}
		
		if(!dp[1][n])
		{
			cout<<"No"<