数据结构课程设计之简单计算器的实现
一、问题陈述
从键盘上输入一算术表达式(中缀白大师),包括圆括号,计算出表达式的值。
要求:
- 程序对所输入的表达式作简单判断,如有错给出提示;
- 实现算术四则运算(
+、-、*、/)和平方(^)运算,能处理双目运算符:+和-; - 能将中缀算术表达式转换成后缀表达式并输出,并输出运算结果。
二、概要设计
2.1 概要简述
中缀表达式转为后缀表达式,从左到右遍历中缀表达式的每个数字和符号,若是数字就输出,即成为后缀表达式的一部分;若是符号,则判断其与栈顶符号的优先级,是右括号或优先级低于找顶符号(乘除优先加减)则栈顶元素依次出找并输出,并将当前符号进栈,一直到最终输出后缀表达式为止。
后缀表达式也称为逆波兰表达式,计算方法为:新建一个表达式,如果当前字符为变量或者为数字,则压栈,如果是运算符,则将栈顶两个元素弹出作相应运算,结果再入栈,最后当表达式扫描完后,栈里的就是结果。
2.2 存储结构表示
typedef struct {//数字栈结构体
double data[MAXSIZE];
int top;
} opstack;
typedef struct {//符号栈结构体
char data[MAXSIZE];
int top;
} stack;
2.3 详细设计
2.3.1 判断中缀表达式是否合理
//判断中缀表达式是否合理
bool judge_infix(char str[]){
int temp=0;
if(str[0]=='/'||str[0]=='*')
return false;
if(str[strlen(str)-1]<'0'&&str[strlen(str)-1]>'9')
return false;
for(int i=0; i<strlen(str); i++) {
if(str[i]=='(') {
if(i==0&&(str[i+1]=='*'||str[i+1]=='/'))
return false;
else if(str[i-1]>='0'&&str[i-1]<='9')
return false;
temp++;
} else if(str[i]==')') {
if(i==0)
return false;
else if(str[i-1]=='+'||str[i-1]=='*'||str[i-1]=='-'||str[i-1]=='/')
return false;
else if(str[i+1]>='0'&&str[i+1]<='9')
return false;
temp--;
}
}
if(temp==0)
return true;
return false;
}
2.3.2 中缀表达式转换为后缀表达式
-
创建栈
-
从左向右顺序遍历中缀表达式:
- 数字直接输出
- 运算符:
遇到‘(’直接入栈,遇到‘)’将栈中‘(’之后入栈的全部输出,同时‘(’出栈但是不输出。其他符号将符号栈中的元素依次出栈并输出,直到遇到比当前符号优先级更低的符号或者‘(’,将当前符号入栈。
-
将栈中剩余的符号依次输出。
//中缀表达式转后缀表达式
void TranslateExpress(char str[], char exp[]) {
stack s;
char ch, e;
int i=0, j=0;
InitStack(&s);
ch=str[i++];
while(ch!='\0') {
switch(ch) {
case '(':
Push(&s,ch);
break;
case ')':
while (GetTop(s,&e)&&e!='(') {
Pop(&s,&e);
exp[j++]=e;
}
Pop(&s,&e);
break;
case '+':
case '-':
while (!StackEmpty(s)&&GetTop(s,&e)&&e!='(') {
Pop(&s,&e);
exp[j++]=e;
}
Push(&s,ch);
break;
case '*':
case '/':
while(!StackEmpty(s)&&GetTop(s,&e)&&e=='/'||e=='*'||e=='^') {
Pop(&s,&e);
exp[j++]=e;
}
Push(&s,ch);
break;
case '^':
while(!StackEmpty(s)&&GetTop(s,&e)&&e=='^') {
Pop(&s,&e);
exp[j++]=e;
}
Push(&s,ch);
break;
case ' ':
break;
default:
while(ch>='0'&&ch<='9') {
exp[j++]=ch;
ch=str[i++];
}
i--;
exp[j++]=' ';
}
ch=str[i++];
}
while(!StackEmpty(s)) {
Pop(&s,&e);
exp[j++]=e;
}
exp[j]='\0';
}
2.3.3 计算后缀表达式值
- 依次遍历栈
- 检测是否是数字,是数字就压栈,是操作符从栈中依次取出当前操作数的右操作数和左操作数与当前操作符进行运算,结果压栈。
- 遍历结束,运行结果就是栈顶元素。
//计算表达式值
double ComputeExpress(char a[]) {
opstack s;
int i=0, value;
float x1, x2, result;
s.top=-1;
while (a[i]!='\0') {
if(a[i]!=' '&&a[i]>='0'&&a[i]<='9') {
value=0;
while (a[i]!=' ') {
value=10*value+a[i]-'0';
i++;
}
s.top++;
s.data[s.top]=value;
} else {
switch(a[i]) {
case '+':
x1=s.data[s.top--];
x2=s.data[s.top--];
result=x1+x2;
s.data[++s.top]=result;
break;
case '-':
x1=s.data[s.top--];
x2=s.data[s.top--];
result=x2-x1;
s.data[++s.top]=result;
break;
case '*':
x1=s.data[s.top--];
x2=s.data[s.top--];
result=x1*x2;
s.data[++s.top]=result;
break;
case '/':
x1=s.data[s.top--];
x2=s.data[s.top--];
result=x2/x1;
s.data[++s.top]=result;
break;
case '^':
x1=s.data[s.top--];
x2=s.data[s.top--];
result=pow(x2,x1);
s.data[++s.top]=result;
break;
}
i++;
}
}
if(!s.top!=-1) {
result=s.data[s.top];
s.top--;
if(s.top==-1)
return result;
else {
printf("表达式错误!");
//exit(-1);
}
}
}
三、测试与运行
3.1 判断表达式是否正确
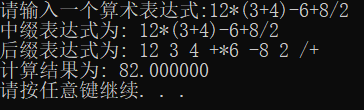
3.2 简单四则运算
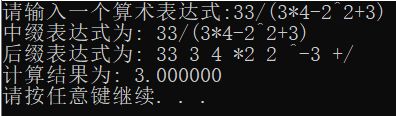
3.3 含平方运算
四、代码实现
#include