谷歌公司经典面试题扔鸡蛋的详细解读—动态规划（二）

---

——————————————–　
　　上一篇博客中咦非常通俗的语言讲解了在只有两个鸡蛋的鸡蛋的情况下如何最快的找到鸡蛋摔碎的临界点（这只是个题目，千万别尝试吆，否则一层楼应该就行了）。
传送门：谷歌公司经典面试题扔鸡蛋的详细解读（一）
　　接下来，题目进阶，如何利用动态规划来求解扔鸡蛋的问题。
　　既，有M层楼/N个鸡蛋，再来找鸡蛋不碎的临界点，需要尝试的次数？

首先要说的是到底啥是动态规划？

　　动态规划 英文 Dynamic Programming，是求解决策过程最优化的数学方法，后来沿用到了编程领域。
　　动态规划的大致思路是把一个复杂的问题转化成一个分阶段逐步递推的过程，从简单的初始状态一步一步递推，最终得到复杂问题的最优解。
　　动态规划解决问题的过程分为两步：
1，寻找转态转移方程式
2，利用状态转移方程式自底向上求解问题

那么，怎样找到状态转移方程式呢？

　　在上一篇博客中，我们只有两个鸡蛋，在一百层楼中进行试验，找到了一个规律，即在假设存在最优解的情况下，最优解是X次，那么第一次进行尝试的楼层就应该是X层。（详细请参看上一篇博客）
　　那么，这个规律在三个以上鸡蛋的条件上还能否适用呢？

　　假设有三个鸡蛋，100层楼，第一个鸡蛋扔在第10层并摔碎了。这时候我们还剩下两个鸡蛋，因此第二个鸡蛋不必从底向上一层一层扔，而是可以选择在第5层扔。如果第二个鸡蛋也摔碎了，那么第三个鸡蛋才需要老老实实从第1层开始一层一层扔。也就是说我们有两次机会来缩小搜索范围，然后用最后一枚鸡蛋来精细搜索。
　　这样的话，最坏的情况是1+1+4=6<10<14（假设法最坏的情况尝试次数）
　　所以说，假设法不再成立。

　　总体思路：
　　这个时候，由于我们手里有多枚鸡蛋，则说明我们有很多种可能性，然后需要将之都列出来，找到规律，然后选出最小的。

　　我们可以把M层楼 / N个鸡蛋的问题，转化成一个函数 F(M,N)，其中楼层数M和鸡蛋数N是函数的两个参数，而函数的值则是最优解的最大尝试次数。

　　假设我们第一个鸡蛋扔出的位置在第X层（1<=X<=M），会出现两种情况：

　　1.第一个鸡蛋没碎
　　那么剩余的M-X层楼，剩余N个鸡蛋，可以转变为下面的函数：
　　F（M-X，N）+ 1，1<=X<=M
　　2.第一个鸡蛋碎了
　　那么只剩下从1层到X-1层楼需要尝试，剩余的鸡蛋数量是N-1，可以转变为下面的函数：
　　F（X-1，N-1） + 1，1<=X<=M
　　
　　整体而言，我们要求出的是 M层楼 / N个鸡蛋 条件下，最大尝试次数最小的解，所以这个题目的状态转移方程式如下：

F（M，N）= Min（Max（ F（M-X，N）+ 1， F（X-1，N-1） + 1）），1<=X<=M
对于这个式子的解释：X是个变化的值，取值从1到M
故也可以写成：
F（M，N）1= Max（ F（M-X，N）+ 1， F（X-1，N-1） + 1），X=1
F（M，N）2= Max（ F（M-X，N）+ 1， F（X-1，N-1） + 1），X=2
F（M，N）3= Max（ F（M-X，N）+ 1， F（X-1，N-1） + 1），X=3
…
…
…
F（M，N）M= Max（ F（M-X，N）+ 1， F（X-1，N-1） + 1），X=M

　　在上述式子的结果中选择最小值，取Min操作。（再有不懂的可以结合下面的例子进行理解或者多看几遍）
如何进行求解？

状态转移方程式有了，如何计算出这个方程式的结果呢？

　　诚然，我们可以用递归的方式来实现。但是递归的时间复杂度是指数级的，当M和N的值很大的时候，递归的效率会变得非常低。
　　根据动态规划的思想，我们可以自底向上来计算出方程式的结果。
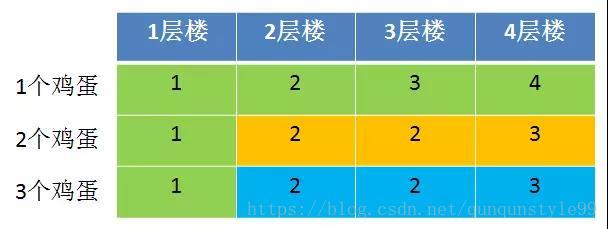
　　何谓自底向上呢？让我们以3个鸡蛋，4层楼的情况试一下。
　　

　　根据动态规划的状态转移方程式和自底向上的求解思路，我们需要从1个鸡蛋1层楼的最优尝试次数，一步一步推导后续的状态，直到计算出3个鸡蛋4层楼的尝试次数为止。

　　首先，我们可以填充第一个鸡蛋在各个楼层的尝试次数，以及任意多鸡蛋在1层楼的尝试次数。

　　原因很简单：
1.只有一个鸡蛋，所以没有任何取巧方法，只能从1层扔到最后一层，尝试次数等于楼层数量。
2.只有一个楼层，无论有几个鸡蛋，也只有一种扔法，尝试次数只可能是1。

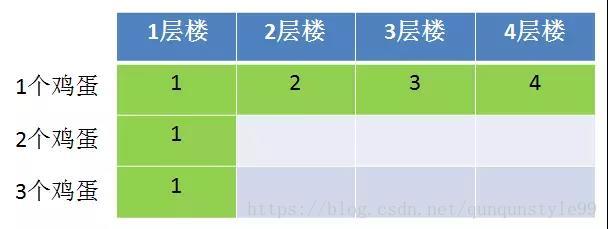
　　2个鸡蛋2层楼的情况，我们就需要带入状态转移方程式了：

F（2,2） = Min（Max（ F（2-X，2）+ 1， F（X-1，2-1） + 1）），1<=X<=2

　　因为X的取值是1和2，我们需要对X的值逐一来尝试：

　　当X = 1时，
F（2,2） = Max（ F（2-1，2）+ 1， F（1-1，2-1） + 1）） = Max（ F（1，2）+ 1， F（0，1） + 1） = Max（1+1, 0+1） = 2

　　当X = 2时，
F（2,2） = Max（ F（2-2，2）+ 1， F（2-1，2-1） + 1）） = Max（ F（0，2）+ 1， F（1，1） + 1） = Max（0+1, 1+1） = 2

　　因此，无论第一个鸡蛋先从第1层扔，还是先从第2层扔，结果都是尝试2次。
　

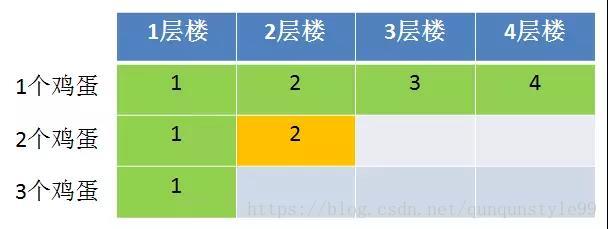
　　接下来我们看一看2个鸡蛋3层楼的情况：

F（2,3） = Min（Max（ F（3-X，2）+ 1， F（X-1，2-1） + 1）），1<=X<=3

　　此时X的取值是1，2，3。我们需要对X的值逐一来尝试：

　　当X = 1时，
F（2,3） = Max（ F（3-1，2）+ 1， F（1-1，2-1） + 1）） = Max（ F（2，2）+ 1， F（0，1） + 1） = Max（2+1, 0+1） = 3

　　当X = 2时，
F（2,3） = Max（ F（3-2，2）+ 1， F（2-1，2-1） + 1）） = Max（ F（1，2）+ 1， F（1，1） + 1） = Max（1+1, 1+1） = 2

　　当X = 3时，
F（2,3） = Max（ F（3-3，2）+ 1， F（3-1，2-1） + 1）） = Max（ F（0，2）+ 1， F（2，1） + 1） = Max（1, 2+1） = 3

　　因此在2个鸡蛋3层楼的情况，最优的方法是第一个鸡蛋在第2层扔，共尝试2次。
　　

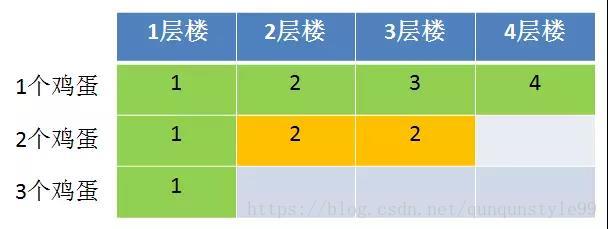
　　依照上面的方式，我们计算出2个鸡蛋4层楼的最优尝试次数，结果是3次。
　　


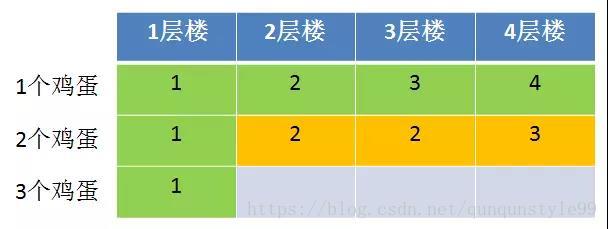
　　同理，我们按照上面的方式，计算出3个鸡蛋在各个楼层的尝试次数，分别是2次，2次，3次。具体计算过程就不再细说。
　　

代码如何实现？

　　根据刚才的思路，让我们来看一看代码的初步实现：

public class Eggs{
public int getMinSteps( int eggNum, int floorNum){
    if(eggNum < 1 || floorNum < 1) {        
        return 0;
    }
    //备忘录，存储eggNum个鸡蛋，floorNum层楼条件下的最优化尝试次数
    int [][] cache = new int[ eggNum+1 ][ floorNum+1 ];
    //把备忘录每个元素初始化成最大的尝试次数
    for(int i=1;i<=eggNum; i++){
        for(int j=1; j<=floorNum; j++)
            cache[i][j] = j;
                }
    for(int n=2; n<=eggNum; n++){
        for(int m=1; m<=floorNum; m++){
            for(int k=1; k//扔鸡蛋的楼层从1到m枚举一遍，如果当前算出的尝试次数小于上一次算出的尝试次数，则取代上一次的尝试次数。
                //这里可以打印k的值，从而知道第一个鸡蛋是从第几次扔的。
                cache[n][m] = Math.min(cache[n][m], 1+Math.max(cache[n-1][k-1],cache[n][m-k]));
            }
        }
    }
    return cache[eggNum][floorNum];
}

public static void main(String[] args) {
    Eggs e = new Eggs();
    System.out.println(e.getMinSteps(5,500));
    }
}

　　这个实现代码，很容易看出来时间复杂度是O（M*M*N）,又因为是对一个二维数组进行操作，故控件复杂度是O（M*N）。但还可以做一点有点，降低控件复杂度到一个数量级。

如何优化呢？

　　我们从状态转移方程式以及上面的表格可以看出，每一次中间状态的尝试次数，都只和上一层（鸡蛋数量-1）和本层（当前鸡蛋数量）的值有关联：

F（M，N）= Min（Max（ F（M-X，N）+ 1， F（X-1，N-1） + 1）），1<=X<=M

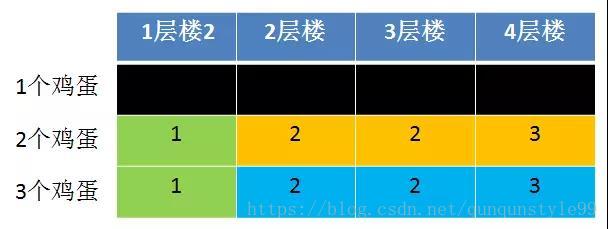
　　比如我们想要求解3个鸡蛋3层楼的最优尝试次数，并不需要知道1个鸡蛋这一层的值，只需要关心2个鸡蛋和3个鸡蛋在各个楼层的值即可。

　　这样一来，我们并不需要一个二维数组来存储完整的中间状态记录，只需要利用两个一维数组，存储上一层和本层的尝试次数就足够了。

　　请看优化版本的代码：

public class EggsOptimized {
public int getMinSteps(int eggNum, int floorNum){
    if(eggNum < 1 || floorNum < 1) {
        return 0;
    }
    //上一层备忘录，存储鸡蛋数量-1的floorNum层楼条件下的最优化尝试次数
    int[] preCache =  new int[floorNum+1];
    //当前备忘录，存储当前鸡蛋数量的floorNum层楼条件下的最优化尝试次数
    int[] currentCache = new int[floorNum+1];
    //把备忘录每个元素初始化成最大的尝试次数
    for(int i=1;i<=floorNum; i++){
        currentCache[i] = i;
    }
    for(int n=2; n<=eggNum; n++){
        //当前备忘录拷贝给上一次备忘录，并重新初始化当前备忘录
        preCache = currentCache.clone();
        for(int i=1;i<=floorNum; i++){
            currentCache[i] = i;
        }
        for(int m=1; m<=floorNum; m++){
            for(int k=1; k//扔鸡蛋的楼层从1到m枚举一遍，如果当前算出的尝试次数小于上一次算出的尝试次数，则取代上一次的尝试次数。
                //这里可以打印k的值，从而知道第一个鸡蛋是从第几次扔的。
                currentCache[m] = Math.min(currentCache[m], 1+Math.max(preCache[k-1],currentCache[m-k]));
            }
        }
    }
    return currentCache[floorNum];
}

public static void main(String[] args) {
    EggsOptimized e = new
    EggsOptimized();
    System.out.println(e.getMinSteps(5,500));
    }
}