史上最全的贝塞尔曲线(Bezier)全解(一):初识贝塞尔曲线
作为一个有只志向的码农,除了知道一些基本的知识够自己努力搬砖以外,还应该get一些更炫酷的技能,用更优雅的姿势进行搬砖;想要实现一些十分炫酷的效果,贝塞尔曲线就必须进行一些研究了;
最近一段时间,我对贝塞尔曲线进行了部分的研究,因此就打算写贝塞尔曲线系列的文章来记录自己的研究;
规矩我都懂 !
我明白,必须先上图,要不然大家都没兴趣看下去
先看比较简单的,贝塞尔曲线的一阶和二阶的应用
看到二阶的贝塞尔曲线有没有感觉很眼熟,没错,360的下火箭弹射时候的小弹弓,还有滑动控件的阴影提示;以前的时候很多小伙伴跟我说这要计算多少数据啊,完全没办法实现啊,现在有了贝塞尔曲线,可以很简单的实现这一个功能;
不过完全不能这样满足啊,接下来还有更复杂一些的曲线
没错,这个就是三阶的使用,有没有感觉路线更加复杂,不过还好,使用贝塞尔去玩完全可以轻松实现;对了,还有一个心在沿着曲线移动,看到这里,小伙伴们肯定会想到满屏幕的心在飞的场景,放心,这个我也实现了,在接下来的文章里,我会一一进行讲解;
图片看完了,现在简单了解贝塞尔曲线
Bézier curve(贝塞尔曲线)是应用于二维图形应用程序的数学曲线。 曲线定义:起始点、终止点(也称锚点)、控制点。通过调整控制点,贝塞尔曲线的形状会发生变化。 1962年,法国数学家Pierre Bézier第一个研究了这种矢量绘制曲线的方法,并给出了详细的计算公式,因此按照这样的公式绘制出来的曲线就用他的姓氏来命名,称为贝塞尔曲线。
以下公式中:B(t)为t时间下 点的坐标;
P0为起点,Pn为终点,Pi为控制点
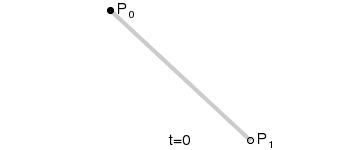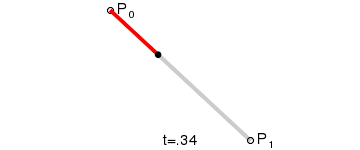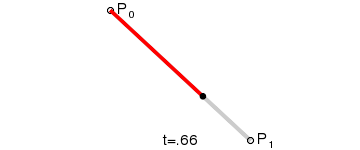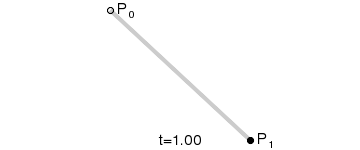
一阶贝塞尔曲线(线段):
意义:由 P0 至 P1 的连续点, 描述的一条线段
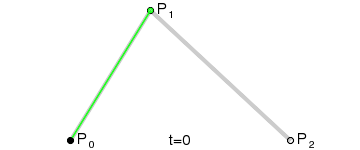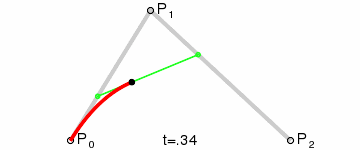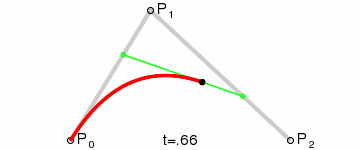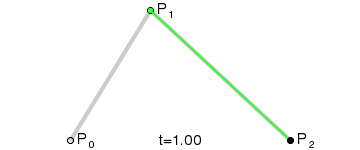
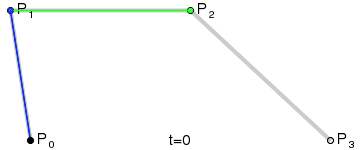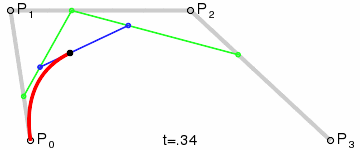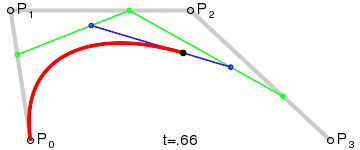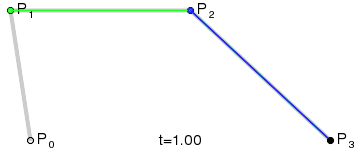
二阶贝塞尔曲线(抛物线):
原理:由 P0 至 P1 的连续点 Q0,描述一条线段。
由 P1 至 P2 的连续点 Q1,描述一条线段。
由 Q0 至 Q1 的连续点 B(t),描述一条二次贝塞尔曲线。
经验:P1-P0为曲线在P0处的切线。
三阶贝塞尔曲线:
通用公式:
利用贝塞尔曲线的这些特性,我们可以画出很多炫酷的曲线,所以贝塞尔曲线还是值得我们去研究学习的;
但是这些完全记不住啊!!!
没关系,可以很负责的说,我也是!!!!!
上面的曲线完全是来自http://blog.csdn.net/tianhai110/article/details/2203572
所以,如果你的数学和我一样是体育老师教的,就忘记这些吧,跟我一起看看android中是实现一条贝塞尔曲线的,android已经帮我们实现好了,剩下的就需要我们进行简单使用,具体的使用,就看下一篇中讲解
最后附上源码:https://github.com/sangxiaonian/BezierIntroduce.git