数据结构-----最大堆的实现
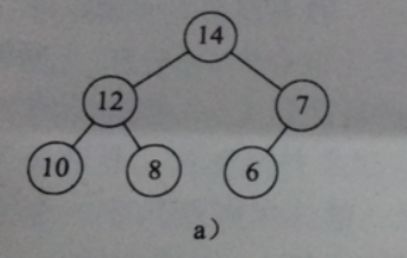
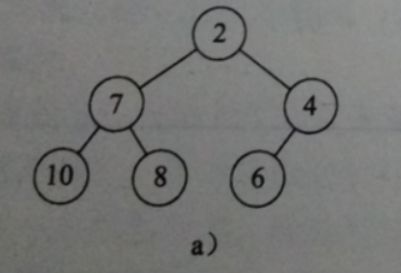
定义:一棵大根树(小根树)是这样一棵树,其中每一个节点的值都大小(小于)或等于其子节点(如果有子节点的话)的值。
一个大根堆(小根堆)既是大根树(小根树)也是完全二叉树。
大根堆
小根堆
本篇主要实现大根堆的初始化,插入以及删除操作。
在实现这些之前,先来简单介绍一下大根堆类的主要数据成员:
私有成员变量:
heap:一维数组,用于存储堆中的元素;
heapSize:整型变量,用于记录堆中元素个数;
arrayLength:整形变量,用于记录堆最大容量,即最多可以容纳多少个元素;
公有成员函数:
initialize(T* ,int):初始化最大堆,第一个形参为初始化的数组,第二个形参为元素个数;
remove(int);删除最大堆中特定元素;
push(const T&);添加新元素;
私有成员函数:
changeArrayLength(T*, int):当实际容量等于额定容量时,扩充额定容量;
adjust(T&,int, int):用于调整堆结构的函数,插入删除和初始化都会用到;
堆虽然也是二叉树,但本例中没有使用构建树的方式(即用节点指针)来构建最大堆,而是用数组的方式存储元素,这样我们假设数组[1:heapSize]用来存储堆元素,而对堆中元素进行调整的过程就是改变元素在数组中位置的过程。
另外需要明确的是,1是根节点的下标,heapSize/2是最后一个节点的父节点下标。
对于某一个节点下标n来说,如果2*n<=heapSize,则2*n是该节点左孩子的下标;
如果2*n+1<=heapSize,则2*n+1是该节点右孩子的下标。
首先来看一下初始化操作的实现,传入的参数为一维数组和元素个数。
步骤1:用参数的数组初始化堆中数组heap,用第二个参数初始化堆中元素个数heapSize;
步骤2:从最后一个节点的父节点开始(heapSize/2),一个个循环,每次循环结束节点索引减一。即第一次是heapSize/2,第二次则是heapSize/2-1,第三次是heapSize/2-2,一直循环到1。暂且叫步骤2为外层循环,该循环是逐个向上。每循环完一次都确保以该下标的节点为根节点的子树是一个最大堆。
步骤3:在步骤2中的每一次循环中(内层循环),逐层向下索引,同时比较当前结点和其子节点的大小,将大节点作为子树的根节点,将原先的根节点下移到子树的位置。直到索引到达heapSize。与步骤2不同,步骤3是逐层向下索引,即某一次索引为n,则下一次是2*n。
template
void maxHeap::initialize(T* theHeap, int theSize)
{
delete[] heap; //删除堆中原先的元素
heap = theHeap; //指针赋值,将参数中数组的元素赋值给堆
heapSize = theSize; //元素个数赋值
//执行循环,从最后一个节点的父节点开始,逐个向上,外层循环
for(int root = heapSize/2; root >= 1; --root)
{
T theElement = heap[root]; //保存外层循环的当前结点,每次都可以理解为给这个值找位置。
//内层循环开始,给theElement找位置,将大的上移,大节点原先的位置变成空位置。
int currentNode = root; //始终是空位置的下标,也是child下标的父节点位置
int child = 2*root; //当前结点左孩子下标
while(child <= heapSize)
{
if(child < heapSize && heap[child+1] > heap[child])
++child; //令child指向值较大的孩子
//如果theElement比两个孩子都大,那么就证明找到位置
if(theElement > heap[child])
break;
//如果没有找到,将大的节点放在空位置上,大节点原先的位置变为空位置
heap[currentNode] = heap[child];
current = child;
//更新孩子下标,继续向下寻找位置
child *= 2;
}
}
//找到位置,将theElement放在空位置上
heap[currentNode] = theElement;
} 接下来是插入操作,参数是要插入的值theElement,原理同初始化一样,也是为theElement找位置,只是开始的位置不是heapSize/2,而是(++heapSize)/2。此时空位置是heapSize。
步骤1:检查数组容量,如果数组满了,则需要扩充数组大小。
步骤2:堆元素个数加一。
步骤3:比较theElement和当前节点大小,如果theElement大,则把当前结点移动到空位置上,把该节点原先的位置设为空位置。继续向上寻找。
template
void maxHeap::push(const T& theElement)
{
//检测堆是否已满,若满则需要扩充
if(heapSize == arrayLength - 1)
{
changeArrayLength(heap, 2*heapSize);
heapSize *= 2;
}
int currentNode = ++heapSize; //堆元素个数加一,空位置为末尾下标
//从下到上一层一层比较,把小节点下移,空位置上移。
//直到空位置的父节点比theElement大,子节点比theElement小
while(currentNode != 1 && heap[currentNode/2] < theElement)
{
heap[currentNode] = heap[currentNode/2];
currentNode /= 2;
}
heap[currentNode] = theElement;
} 最后是删除操作,参数是要删除的下标索引。删除后,以该位置为根节点的子树已经不是最大堆,只需要对这一小部分进行调整。
原理依旧相同,把要删除的那个下标设为空位置。逐层向下寻找位置,把大节点上移,空位值下移。
步骤1:取出末尾下标的元素theElement,并将堆元素个数减一。
步骤2:在以删除节点为根节点的子树中为theElement找位置。
template
T maxHeap::remove(int index)
{
//判断下标是否合法
if(index < 1 || index > heapSize)
throw heapError("Error: the index is illegal");
T theElement = heap[heapSize--]; //取出最后一个元素,同时元素个数减一
int currentNode = index; //始终指向空位置,也是child的父节点
int child = 2 * index;
while(child <= heapSize)
{
//令child是较大孩子的下标
if(child < heapSize && heap[child+1] > heap[child])
child++;
//如果theElement大,则说明找到位置存放theElement了
if(theElement > heap[child])
return;
//若没找到,继续向下寻找
heap[currentNode] = heap[child];
currentNode = child;
child *= 2;
}
heap[currentNode] = theElement;
return theElement;
}