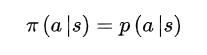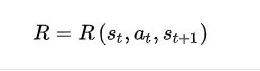《ARPG游戏深度强化学习 》序贯决策问题、完成ARPG世界里的游戏代码实践

序贯决策问题

图示：

马尔科夫决策过程

序贯决策，主要的方法是：马尔科夫决策过程。

一个马尔可夫过程叫：MDP。
一个MDP由一个五元组构成：S A P R r

• S 是所有状态的集合
  

• A 是所有动作的集合
  

• P 是某状态S’在某A‘动作下的转移概率
  
  策略P就是在状态S下做A的概率多大。

• R 是奖励
  

• r 是回报有时候也用G标示（gain）
  

当前状态，当前要做的动作，以及下一个状态，三者共同决定环境反馈给智能体，什么样的R（奖励），通常R是标量函数，返回一个标量，标量对应的向量，向量自带方向标量是一个值。

例如：
王者荣耀：R（还有200点血，施展加血魔法magic1，有400点血）=5
当前要做的动作是：施展加血魔法magic1，就是加血，下一个状态，加血.
这个5是自己认为可以设计的。

回报的概念就是：每个动作执行后，所有的R累加。回报是评估当前MDP的一个得分。

model-free和model-based（有模型的方法和无模型的方法）

什么叫有模型的方法呢？

比如百度地图 能够瞬间给出A到B地点的 最短路径 ，是站在上帝视角上 得到了全局的城市交通数据 然后 直接最短路径求解 。

**无模型的方法，往往是用于不可能站在上帝视角，信息不够全的各种即时策略方法 **

蒙特卡罗法（Monte Carlo）

Monte Carlo 方法 适用于工程学 和各个行业领域 以及数学问题 。

用MC去解决问题 主要有经典的三个步骤：

• 构造概率过程
• 实现从已知概率分布中进行抽样
• 建立各种估计量

例如：

算一个不规则的 2D 面积 。

微积分：

用多个长方形切割开 这个不规则凹封闭曲线
只要长方形的宽足够的短，把各个长方形的面积累加 ，就非常接近这个不规则封闭曲线内部的面积 。

用Monte Carlo

直接拿200粒米 ，随机均匀的撒在方块内（撒出方块的不统计），最后 只要分别统计 在封闭曲线内的米的数量 A 和 在方块内 但是不在曲线内的米B ， 这样 A/ (A+B) = 曲线内面积/方块面积，方块面积* A/ (A+B) = 曲线内面积。

我们以上的方法 用了同样的三个步骤：

• 构造概率过程：已知这样的曲线；
• 从已知概率分布抽样：均匀撒米，统计米的多少；
• 建立估计量：用估计量测算目标面积。

AlphaGo 也用到了MC方法：

先是随机走（均匀撒米）
建立概率分布抽样（匹配棋盘结果，生成蒙特卡罗搜+
建立估计量：得到比较好的决策依据

MC方法特别适合 没有明显规律 或者规律很复杂 没有解析解的问题

on-policy off-policy

区分的方式就是：

on-policy ：agent(智能体）从环境学习的策略和它与环境交互的策略，一样。

off-policy：agent（智能体）从环境学习的策略和它与环境交互的策略，不一样。

on-policy例子：

如果每次了解到周围最好的动作值，就直接走过去。并且学习策略也一样（告诉自己的大脑，自己以后也要这样更新自己的价值表）

这种 和环境的交互策略 和 自己学习更新自己的行动决策依据的表 的 方案是一样的 就是on-policy。

off-policy 例子：
眼前有一块红烧肉，我脑中模拟自己吃了一口，模拟吃的时候很好吃，然后更新了一下策略表，告诉自己，吃这块红烧肉会得到奖励。关键是 ： 我只是脑袋里模拟的吃了一口。这不代表和环境交互 ，真正的环境交互是：我实际怎么做了？

如果脑袋里模拟吃了一口后，更新策略表，告诉自己，吃红烧肉可以得到奖励。（这叫【学习】）如果是on-policy，那就会直接和环境交互的过程中，也会实际吃一口红烧肉这个动作。但是如果是off-policy，则可能采取和【学习】的时候模拟的做法不一样，就是说，学习的策略并不用于直接决策用于执行如何和环境交互。这个时候 ，off-policy的做法是，虽然吃红烧肉比当前状态s下做别的动作回报多。但是我不一定选它这叫off-policy ，我保留了 一定的概率 我会随机选 或者其他方法 。

这种方法的robust（鲁棒性）非常强。
大家知道，我们吃红烧肉，立马获得了当前状态下能够获得的最好R（回报），但是不代表吃红烧肉在未来若干个时间内是最好的选择。（比如带来了增肥，脂肪肝，三高)。如果按on-policy ，当前学习的策略可能并不代表未来 。但是智能体如果用on-policy，就会过于相信自己学到的眼前的东西。off-policy的智能体，则会说：虽然吃红烧肉我感觉是当前状态的最佳回报选择，但是我还是保留不吃的可能性，避免后面碰到更多的红烧肉，把我引入了某种深渊(三高和肥胖、亚健康和脂肪肝、肝癌、死亡）。这样 ，就不会一直吃红烧肉，偶尔还会不吃，去做别的事。这样才会有更多的机会学到新的可能性和探索新的优化。

几乎现在所有的深度强化学习应用，都用到了Q-Learning这一类的，off-policy的算法

Q-Learning

Q-Learning 就是一个数学公式 比较简洁。

• S代表当前状态
• a代表了当前状态所采取的行动
• S’代表S在a行动后跳转到的下一个状态
• Q(S,A)代表 Q估值
• γ 决定未来奖励的重要性的程度

由公式看出：

s，a 对应的 Q 值等于 即时奖励 结合 未来奖励的 折扣discount

具体落地到怎么执行 可以用 bellman 公式：

• r是智能体在s状态上采取a行动的奖励
• γ 是 discount度

举例：

第一步：
Q(饿了，吃红烧肉）= Reward(饿了，吃红烧肉) + Discount*max(Q(不饿了,吃红烧肉))
我们定义了如下的 MDP

S={饿了，不饿，很饱，超级胖，三高}
A={吃红烧肉，运动，吃素，看书}
choose_action(饿了，吃红烧肉)=不饿
R(饿了，吃红烧肉)=10
choose_action(不饿，吃红烧肉）=很饱
R(不饿，吃红烧肉）=0
choose_action(很饱，吃红烧肉）=超级胖
R(很饱，吃红烧肉)=-5
choose_action(超级胖，吃红烧肉）=三高
R(超级胖，吃红烧肉)=-20

第二步：
Q(饿了，吃红烧肉）= R(饿了，吃红烧肉) + Discountmax( R(不饿了,吃红烧肉) + Discountmax(Q(很饱，吃红烧肉)) )

再继续展开 就是更进一步 把 Q(很饱，吃红烧肉) 展开，其中 Discount 如果=1 ，那么 未来的所有步骤获得回报值 都会不打折扣的累加到当前的Q。如果Discount =0.6 ，就是说 每往后一步 回报值对当前Q估计决策 的 累加 逐步影响递减。

如何更新Q-Table
Q-Table就是S(s,a)

1. 首先随机初始化S(s,a)表为一些比较小的随机数
2. repeat：（起点）
3. 基于s状态选择一个行动
4. 接受奖励r以及跳转到新的状态s’
5. Q(s,a) <- 老Q(s,a) 值+ alpha*( y- 老Q(s,a)值 )
6. 直到 学习结束

其中y= R + discount*max Q(S’,a)
Q是一张表，所以用Q-table 表示 ，老Q(s,a)值 的意思是 表还没更新的时候 对应的 Q(s,a)值 ，等同于python的 =。

Q-Table的更新 就是agent学习的过程，而agent每一次决策，则是 选取 argmax Q(s, )。
argmax 的意思是 比如 ：集合A={2,5,1,3,6} max (A) = 6。argmax(A) = 4 。因为从0数起 ， 6在序号4 。index=4 。argmax(A)的意思是 A里的最大值对应的 index

完成南理ARPG世界里的游戏

import numpy as np
import pandas as pd
import time 



np.random.seed(2) #reproducible


class QLearning():
    T=10  #target
    W=-2  #wall
    F=1 #flower
    M=0# Moving road
    

    MAP=[[W,W,W,W,W,W,W,W],
         [W,0,0,0,0,0,F,W],
         [W,0,0,0,0,0,F,W],
         [W,0,W,W,W,0,W,W],
         [W,0,W,T,0,0,F,W],
         [W,0,W,W,W,0,F,W],
         [W,0,0,0,0,0,0,W],
         [W,W,W,W,W,W,W,W]]
    N_STATES =(len(MAP),len(MAP[0]))

    FLOWER=1
    ROAD=0
    
    ACTIONS =['left','right','up','down']
    EPSILON = 0.7
    ALPHA=0.1
    LAMBDA =0.9
    MAX_EPISODES=13
    FRESH_TIME=0.1

    def build_q_table(self,n_states,actions):
    	table =pd.DataFrame(
    		np.zeros((n_states,len(actions))),
    		columns=actions,
    		)
    	print(table)
    	return table
    
    def choose_action(self,state,q_table):
        state_actions=q_table.iloc[state[0]*self.N_STATES[0]+state[1],:]
        if(np.random.uniform()>self.EPSILON) or (state_actions.all()==0):
            action_name=np.random.choice(self.ACTIONS)
        else:
            action_name=state_actions.argmax()
        return action_name
    
    def get_env_feedback(self,S,A):


        if A=='right' and self.MAP[S[0]+1][S[1]]!=-2:
            S_=(S[0]+1,S[1])
            R=self.MAP[S[0]+1][S[1]]
        elif A=='left' and self.MAP[S[0]-1][S[1]]!=-2:
            S_=(S[0]-1,S[1])
            R=self.MAP[S[0]-1][S[1]]
        elif A=='up' and self.MAP[S[0]][S[1]-1]!=-2:
            S_=(S[0],S[1]-1)
            R=self.MAP[S[0]][S[1]-1]
        elif A=='down' and self.MAP[S[0]][S[1]+1]!=-2:
            S_=(S[0],S[1]+1)
            R=self.MAP[S[0]][S[1]+1]
        else:
            R=0
            S_=S

        if R==self.F:
            R=0

        return S_,R
    
    def update_env(self,S,episode,step_counter):

# encoding: utf-8 
        n_str=self.N_STATES[0]+1
        BOARD=''
        env_list=([BOARD]*self.N_STATES[1]+['\n'])*self.N_STATES[0]

        for i in range(self.N_STATES[0]):
            for j in range(self.N_STATES[1]):
                if self.MAP[i][j]==self.M:
                    env_list[i*n_str+j]=''
                elif self.MAP[i][j]==self.F:
                    env_list[i*n_str+j]=''
                elif self.MAP[i][j]==self.T:
                    env_list[i*n_str+j]=''
                        

        import sys
        env_list[S[0]*n_str+S[1]]=''
        interaction=''.join(env_list)
        #print('\r{}'.format(interaction),end='')
            
        sys.stdout.write('\r' + interaction)
        print('\n-------------------\n',end='')
            
        time.sleep(self.FRESH_TIME)
        
        if self.MAP[S[0]][S[1]]==self.T:
            interaction='Episode %s:total_steps=%s'%(episode+1,step_counter)
            #print('\r{}'.format(interaction),end='')
            
            sys.stdout.write('\r' + interaction)
            #sys.stdout.flush()
            
            time.sleep(2)
            print('\n-------------------',end='')
            
            

            
            
            
    def rl(self):
    
        print(self.N_STATES)
        q_table=self.build_q_table(self.N_STATES[0]*self.N_STATES[1],self.ACTIONS)
        for episode in range(self.MAX_EPISODES):
            self.step_counter=0
            S=(1,1)  #start position
            is_terminated=False

            while not is_terminated:
                self.update_env(S,episode,self.step_counter)
                A=self.choose_action(S,q_table)
                S_,R=self.get_env_feedback(S,A)
                q_predict=q_table.ix[S[0]*self.N_STATES[0]+S[1],A]
                if R!=self.T:
                    q_target=R+self.LAMBDA*q_table.iloc[S_[0]*self.N_STATES[0]+S_[1],:].max()
                else:
                    q_target=R
                    is_terminated=True
                q_table.ix[S[0]*self.N_STATES[0]+S[1],A]+=self.ALPHA*(q_target-q_predict)
                S=S_
                self.step_counter+=1
            self.update_env(S,episode,self.step_counter)    
        return q_table

if __name__=="__main__":
    
   
    robot=QLearning()
    q_table=robot.rl()
    print('\r\nQ-table:\n')
    print(q_table)       

新增的代码：

    def build_q_table(self,n_states,actions):
     table =pd.DataFrame(
      np.zeros((n_states,len(actions))),
      columns=actions,
      )
     print(table)
     return table

• 其中 n_states 是状态的数量
• actions是行动的集合
• len(actions) 是行动的数量
• np.zeros( A,B) 是返回一个 0矩阵，AxB A行B列 每一个元素都是0
• columns=actions, 的意思是 每一列的列名 分别是 actions动作的名字[‘left’,‘right’,‘up’,‘down’]
• pd 是引入了 panda库
• panda.DataFrame 是数据科学中常用的方法 ，用于构造一个数据表 （ 可以兼容各种数据库以及excel），内置了各种数据格式和输入输出方法

    def choose_action(self,state,q_table):
        state_actions=q_table.iloc[state[0]*self.N_STATES[0]+state[1],:]
        if(np.random.uniform()>self.EPSILON) or (state_actions.all()==0):
            action_name=np.random.choice(self.ACTIONS)
        else:
            action_name=state_actions.argmax()
        return action_name
    

这是 智能体 （猴子） 在状态state 的时候 ，基于q_table 返回一个action_name。

有两种决策方式：

1. 第一种是随机选择一个行动执行
2. 第二种是取Q表中，在s状态下，哪一个动作的Q值最大，就选哪个动作

state[0]*self.N_STATES[0]+state[1] 把 二维的猴子的位置转化为 1维
比如 猴子在 (3,5) 这个位置 ，我们转化为 对应的一维数组在的位置 （就是把第二行接到第一行后面，第三行接在第二行后面 ……）

代码分析：
---------------------------------------------------------------------------------------------------------

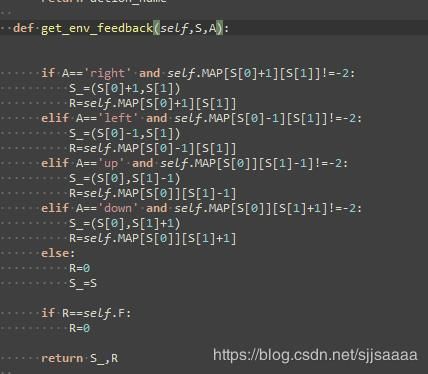
获取环境反馈。
我们根据用户的行为 上下左右动作，把用户跳转到下一个状态 ，如果正好是一面墙 W ，以及 走到各种地方 的奖励 和 下一个状态S_，把下一个状态S_ 和 奖励R 返回出函数 。

---------------------------------------------------------------------------------------------------------

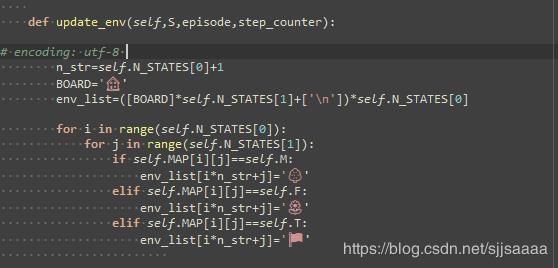
更新环境 就是输出一次地图

---------------------------------------------------------------------------------------------------------

这个过程就是 Q-Learning算法

q_table=self.build_q_table(self.N_STATES[0]*self.N_STATES[1],self.ACTIONS) 首先构造一个q-table，其中第一个参数 是把二维数组 计算一下二维数组总计有多少个元素（位置），二维数组的位置/状态 总数 就是 第一个参数 状态数 ，第二个参数 是 传入行动集合 。

for episode in range(self.MAX_EPISODES): 循环 MAX_EPISODES次

每一个episode 都是猴子从起点 到终点 的一个完整的过程 ，我们每次都让猴子从S=(1,1) #start position 开始 ，is_terminated=False 初始化 设定 没有到终点。

while not is_terminated:如果当前猴子还没到终点状态

self.update_env(S,episode,self.step_counter)更新环境（刷新地图和猴子位置）

A=self.choose_action(S,q_table)猴子根据当前状态位置S 以及当前q_table
选择一个A行动
S_,R=self.get_env_feedback(S,A)环境给予反馈 ，得到下一个状态位置 S_ 以及奖励R

q_predict=q_table.ix[S[0]*self.N_STATES[0]+S[1],A]做一下预测，如果用A行动去走，将会得到什么Q值

        if R!=self.T:
   q_target=R+self.LAMBDA*q_table.iloc[S_[0]*self.N_STATES[0]+S_[1],:].max()

如果当前做了A动作后获得的奖励 ，不是self.T #(Target) ，也就是说还没到终点，目的地猴子更新q_target值 ，否则

     q_target=R
            is_terminated=True

设置当前episode结束

q_table.ix[S[0]*self.N_STATES[0]+S[1],A]+=self.ALPHA*(q_target-q_predict) 更新Q表的Q(s,a)

            `S=S_`当前状态更新为最新状态
                            `self.step_counter+=1`当前episode下，step+1 ，用于显示当前一次任务用了多少步 

self.update_env(S,episode,self.step_counter) 更新环境

所有episode 结束后 return q_table返回Q表

---------------------------------------------------------------------------------------------------------

if __name__=="__main__":
    
   
    robot=QLearning()
    q_table=robot.rl()
    print('\r\nQ-table:\n')
    print(q_table)       

主函数
智能体创建QLearning对象，智能体开始迭代N次 robot.rl()，并且返回q_table

run后的Q-table：

代表根据 每个状态 对应有四种走法 上下左右 下的q值

当第13次episode结束后 ,猴子学会了在16步内 从起点到终点 ，虽然距离绝对最优解 10步，还有差距 ，但是这只是让猴子尝试了从零开始玩13盘这个游戏，如果再多走几盘 基本上会越来越接近最优解。

我们来看猴子第一次玩这个游戏 ，找到目标用了95步。

第二次 用了102步，说明在q-learning算法前期 ，效果并不稳定但是后面却能够收敛的越来越快。

修改了这几个参数：都增大了，

ALPHA=0.5
LAMBDA =1.1
MAX_EPISODES=15

第一次还是95，第二次还是102

当把 参数设置成 FRESH_TIME=0.01
进行到了13次：

作业

作业1#深度的去查找model-free和model-based的案例，对比细微差别和总结。

Model-based RL
一种方法就是Model-based方法，让agent学习一种模型，这种模型能够从它的观察角度描述环境是如何工作的，然后利用这个模型做出动作规划，具体来说，当agent处于s1s1状态，执行了a1a1动作，然后观察到了环境从s1s1转化到了s2s2以及收到的奖励rr, 那么这些信息能够用来提高它对T(s2|s1,a1)T(s2|s1,a1)R(s1,a1)R(s1,a1)的估计的准确性，当agent学习的模型能够非常贴近于环境时，它就可以直接通过一些规划算法来找到最优策略，具体来说：当agent已知任何状态下执行任何动作获得的回报，即R(st,at)R(st,at)已知，而且下一个状态也能通过T(st+1|st,at)T(st+1|st,at)被计算，那么这个问题很容易就通过动态规划算法求解，尤其是当T(st+1|st,at)＝1T(st+1|st,at)＝1时，直接利用贪心算法，每次执行只需选择当前状态stst下回报函数取最大值的动作(maxaR(s,a|s=st)maxaR(s,a|s=st))即可，这种采取对环境进行建模的强化学习方法就是Model-based方法。

Model free RL
但是，事实证明，我们有时候并不需要对环境进行建模也能找到最优的策略，一种经典的例子就是Q-learning，Q-learning直接对未来的回报Q(s,a)Q(s,a)进行估计，Q(sk,ak)Q(sk,ak)表示对sksk状态下执行动作atat后获得的未来收益总和E(∑nt=kγkRk)E(∑t=knγkRk)的估计，若对这个Q值估计的越准确，那么我们就越能确定如何选择当前stst状态下的动作：选择让Q(st,at)Q(st,at)最大的atat即可，而Q值的更新目标由Bellman方程定义，更新的方式可以有TD（Temporal Difference）等，这种是基于值迭代的方法，类似的还有基于策略迭代的方法以及结合值迭代和策略迭代的actor-critic方法，基础的策略迭代方法一般回合制更新（Monte Carlo Update），这些方法由于没有去对环境进行建模，因此他们都是Model-free的方法

作业2#找到蒙特卡罗方法在各领域的应用案例3个。

蒙特卡罗方法在金融工程学，宏观经济学，生物医学，计算物理学(如粒子输运计算、量子热力学计算、空气动力学计算)等领域应用广泛。

蒙特卡罗模型是利用计算机进行数值计算的一类特殊风格的方法, 它是把某一现实或抽象系统的某种特征或部分状态, 用模拟模型的系统来代替或模仿, 使所求问题的解正好是模拟模型的参数或特征量, 再通过统计实验, 求出模型参数或特征量的估计值, 得出所求问题的近似解。目前评价不确定和风险项目多用敏感性分析和概率分析,但计算上较为复杂,尤其各因素变化可能出现概率的确定比较困难。蒙特卡罗模型解决了这方面的问题,各种因素出现的概率全部由软件自动给出,通过多次模拟,得出项目是否应该投资。该方法应用面广, 适应性强。

在军事方面：射击椭圆面目标时必须导弹数的蒙特卡洛模拟计算。

蒙特卡罗法在防辐射领域的应用。

蒙特卡洛在强化学习中的应用：

1. 完美信息博弈：围棋、象棋、国际象棋等。

2. 非完全信息博弈：21点、麻将、梭哈等。

作业3# on-policy和off-policy各描述2个这样的智能体决策场景。以及查阅这两种方法在实际当中的各种运用。

策略梯度类型的方法不能直接使用off-policy 的原因是因为更新一次策略就会改变，因此必须要重新采样。
on-policy算法的好处

• 直接了当，速度快，劣势是不一定找到最优策略。
• On-policy 算法对于整体的策略的稳定性会有提升，但是会加剧样本利用率低的问题，因为每次更新都需要进行新的采样。
• 很难平衡探索和利用的问题，探索少容易导致学习一个局部最优。而保持探索性则必然会牺牲一定的最优选择机会，而且降低学习效率。
• 其实可以把on-policy看作off-policy的一个特殊情形。

off-policy算法的好处

• 可重复利用数据进行训练，data利用率相对较高，但是面临收敛和稳定性问题。去年，Haarnoja 提出了Soft Actor Critic，极大的提高了Off-policy RL 的稳定性和性能。
• off-policy劣势是曲折，收敛慢，但优势是更为强大和通用。其强大是因为它确保了数据全面性，所有行为都能覆盖。甚至其数据来源可以多样，自行产生、或者外来数据均可。
• 迭代过程中允许存在两个policy，可以很好分离并探索和利用，可灵活调整探索概率。

on-policy算法是在保证跟随最优策略的基础上同时保持着对其它动作的探索性，对于on-policy算法来说如要保持探索性则必然会牺牲一定的最优选择机会。

有一个更加直接的办法就是在迭代过程中允许存在两个policy，一个用于生成学习过程的动作，具有很强的探索性，另外一个则是由值函数产生的最优策略，这个方法就被称作off-policy