台湾大学深度学习课程 学习笔记 lecture4 Word Embeddings

以下内容和图片均来自台湾大学深度学习课程。
课程地址：https://www.csie.ntu.edu.tw/~yvchen/f106-adl/syllabus.html

在之前 lecture2-2 Word Representation 的课程中简单讲解了 Word 处理的传统方法。通过传统方法的局限性引入新的方法 Word Embeddings，从而直接学习得到低维结果，而不是高维学习后再进行降维。

Word Embeddings 有两种方法：word2vec (Mikolov et al. 2013) ，Glove (Pennington et al., 2014)，这节课根据之前的课程，继续介绍。

Word2Vec

Skip-Gram

下面的公式比较复杂，我自己写了都记不住。如果只纠结于公式，反而可能导致不能更好的理解模型本身的含义，建议先去看一下我的另一篇博客，【RNN】理解循环神经网络中的 Skip-Gram ，这篇文章中，没有公式，纯人话解释 Skip-Gram，帮助你先理解模型，再回过头理解公式会清晰很多。

Model

通过这种方法，指定 word 后，一定范围内的其他单词（neighbors
）出现的几率。

其中， wI w I 表示指定的 word， wO w O 表示指定窗口大小 C C 范围内的其他 word。
比如下面例子中的 wt w t 其实就代表 wI w I ，窗口大小 C C 为 m m 。 (wt−m,...,wt−1) ( w t − m , . . . , w t − 1 ) 与 (wt+1,...,wt+m) ( w t + 1 , . . . , w t + m ) 就是 wO w O ，共 2m 2 m 个。

在指定的 word 条件下，指定窗口内其他 word 发生的概率计算公式如下：

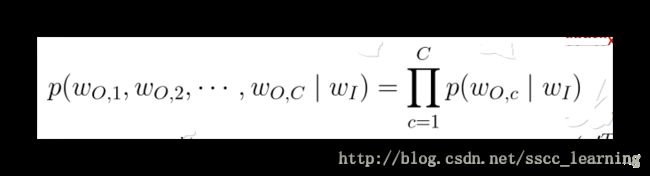
根据最大似然估计，应该使得上面的概率结果最大。对上面公式进行取 log l o g 后添加负号后，得到损失函数的表示公式，目标使损失函数最小。

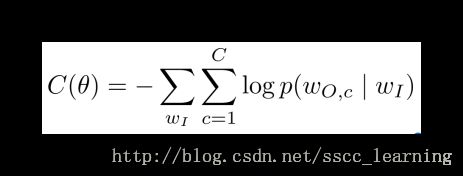
最终输出时，需要将输出层结果进行转换，公式如下，具体含义后面还会详细介绍。

通过上面的内容简单引入公式，介绍了各种符号的含义，接下来会对这些内容进行详细解释。

结构

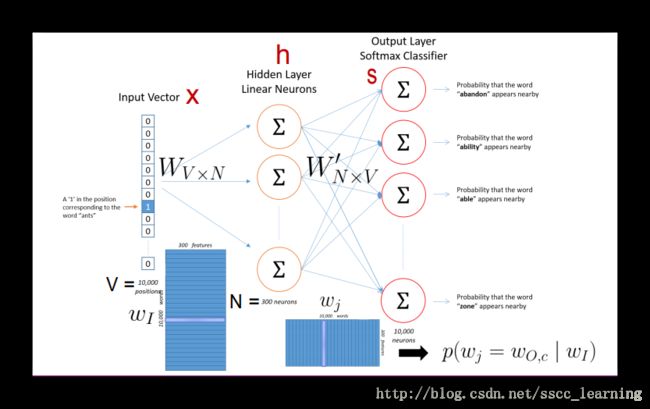
模型的结构很简单，如下图，是一个只有一个隐藏层的神经网络。由于要得到输入的每个 word 出现的概率，所以输入层与输出层神经元数需一致。下图中，输入 x x 和输出层 s s 数量为10000，隐藏层 h h 神经元数为300。

现在对隐藏层权重 W W 转换一下思想，注意转换的仅仅是我们的思想，实际上没有对隐藏层做任何改变。
上面的例子中，输入的 x x 是10000行，后面的隐藏层共300个神经元，所以 W W 是 10000×300 10000 × 300 的矩阵。
实际 xTW x T W 计算的过程，思想其实是像下图左中的样子， W W 每一列与 xT x T 对应相乘后再相加。如何将想法转换成下图右中的模式呢？请看接下来的例子。

由于 x x 是one-hot转换后的，所以在指定的word上是1，其余都是0。这样的话，经过计算后，实际的结果中是把 W W 相应的一行数据给完整保留下来了，其余的都乘以0后都没了，具体见下图。所以，也可以从行的角度看 W W 。

综上所述， h h 的计算结果，其实也就是从 W W 中抽取出来相乘不为0的一行当成结果，可以用向量 vwI v w I 表示。

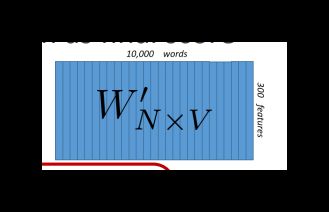
上面说了隐藏层 h h ，下面说一下输出层 s s 。从 h h 到 s s 之间的系数为 W′ W ′ 。
上面说道 s s 输出层共10000个神经元，每个神经元的计算方法如下：

sj=hv′wj s j = h v w j ′

其中， v′wj v w j ′ 是 W′ W ′ 的第 j j 列。

得到 sj s j 后，还需要做最后的转换才是最终输出的结果。转换公式如下，这也是一般多分类 softmax 的计算方法。

下图就上对上面所讲的，从隐藏层到最后输出概率的一个总结。 h h 与 W′ W ′ 的计算结果，经过公式转换得到最后每个 word 的概率。

如果把计算过程放在整体上看，如下图。

损失函数及梯度下降

上面有讲损失函数公式，将 p p 代入进去整理得到下面公式。

使用梯度下降的方法对损失函数进行优化。从右向左，首先看 W′ W ′ 这边。

整理后得到如下公式。

然后是 W W 这边，

整理后得到。

把公式进行简化，简化之后得到下图中红色部分的公式。

其中 j j 是 输入 X X 中 words总数量。从上面的公式中可以看出来，计算量和 j j 相关。当 j j 比较大的时候，计算量会非常大。

为了解决计算的问题，有两种常用的方法：hierarchical softmax 和 sampling 。常用的是sampling。

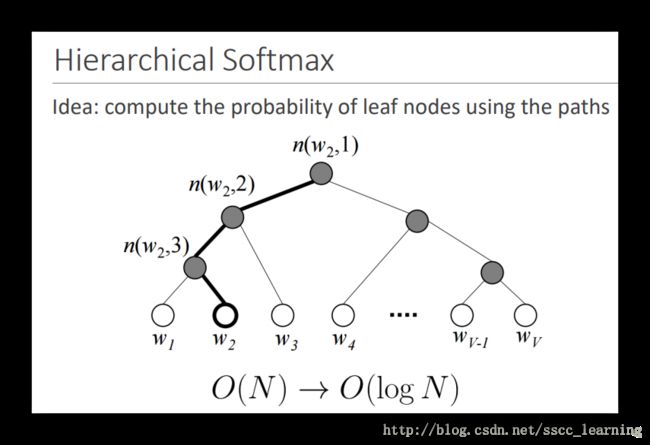
Hierarchical Softmax

采用一些演算法技巧，通过分支结构减少计算的复杂度。

Sampling

抽样是更为常用的减少计算量的方法。可以有效的减少计算量，而且表现效果并不会下降太多。因为是随机选取，每个被选取到的概率相同。不停的迭代后，可以有效地得到结果。

一些不常出现的word有时有着一定作用，但在随机抽样中，却很难被抽到。所以有时就需要增加低频词汇出现的概率。

下面这个方法是一个比较好的经验。将每个word出现概率加上 34 3 4 的指数。比如“is”出现的概率为0.9，那么进行 34 3 4 次方处理后变成了0.92 ，涨了一点。但是看下面的“bombastic”出现概率原来是0.01，处理后变成了0.032，概率涨了3倍多。可以看出，小概率经过处理后增加的比大概率的要高得多。通过这种方法，可以有效地处理小概率时间很难被抽到的问题。

Word2Vec Variants

Word2Vec 还有一些其他的方式，比如CBOW、LM 。具体方法请看下图，其实LM是最早被提出来的，而Skip-gram是不断完善后的样子，所以现在Skip-gram应用是最广泛的。CBOW和Skip-gram正好相反，Skip-gram是给定一个word，预测窗口内其他words，而CBOW是给定窗口内其他words的概率，预测指定word。

方法比较

这里主要是count-based和Direct-prediction之间的比较，之前并没有把所有的方法都讲到。
首先说一下，count-based，顾名思义，这个主要是通过统计学的方法进行计算，这种计算是比较快的。但是得到的结果也只是 “words之间是否同时出现”、“word出现频率” 等信息，无法得到word之间更复杂的关系。
Direct-prediction是通过神经网络方法去自动的估计结果。可以考虑到word之间语义相关的更复杂的关系。但是，并没有应用上统计学的信息，在统计信息上面有所欠缺。

根据上面的额结果就引出了 GloVe 方法，不仅有神经网络，还应用到了统计上面的方法。在一些数据量较小的应用的一般表现较好。

GloVe

co-occurrence probability，意思是一个word wi w i 出现时，另一个word wj w j 也出现的概率。公式如下，其中 X X 表示出现的次数。

现在假设 wi w i 与 wj w j 都与 word x x 有关系，可以计算出 P(x|wi) P ( x | w i ) 与 P(x|wj) P ( x | w j ) ，将这两个结果相除 P(x|wi)P(x|wj) P ( x | w i ) P ( x | w j ) ，就得到了ratio。通过下面的例子可以看出，这个公式结果具有一些明显的规律。当 wi w i 与 wj w j 含义比较接近时，他们的ratio就接近1。当含义不接近时，ratio就会较大或较小。

所以想要了解两个word wi w i 与 wj w j 之间的关系，可以通过它们共有的另一个word wk~ w k ~ ，经过计算得到ratio值，从而判断 wi w i 与 wj w j 之间的关联。

F(wi,wj,wk~) F ( w i , w j , w k ~ ) 其实就表示 wi w i 与 wj w j 之间的差异关系，所以也可以表示为 F(wi−wj,wk~) F ( w i − w j , w k ~ ) 。
将它们转化成向量表示 F((vWi−vwj)Tv′wk~) F ( ( v W i − v w j ) T v w k ~ ′ ) 。
如果 wi w i 与 wj w j 比较接近，则结果趋向于1，否则会偏大或者偏小，正好可以通过 exp e x p 的公式可以进行转换。

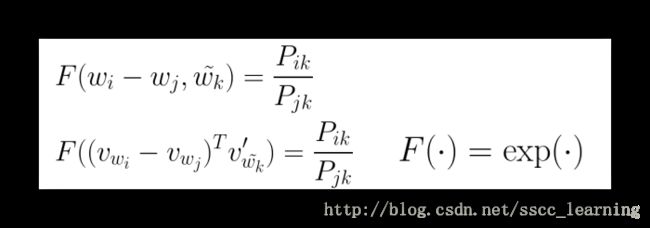
两边取 log l o g 后，进行整理。把 log(Xi) l o g ( X i ) 当成一个常数项，整理进公式。同样也给 wj w j 添加一个常数项。

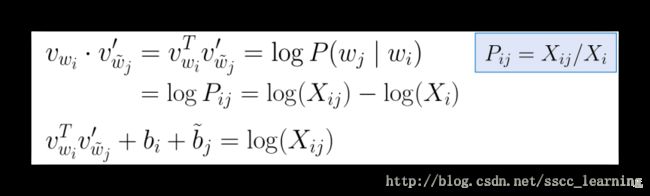
整理后的损失函数中还添加了 f(Xij) f ( X i j ) ，就相当与把统计相关的数据也添加进来进行优化。在比较小的数据集中，也有较好的表现效果。

Word Vector Evaluation

上面讲了word vector构建的方法，接下来说一下word vector的评估方法。

Intrinsic Evaluation 内在

Word Analogies 类比

首先是单词类比，给定两个相关的words “A”和“B”，例如“man”“woman”。是否能推测出“king”对应的是“queen”？
或者给出“king”与其复数“kings”，是否能推测出“queen”对应的“queens”。

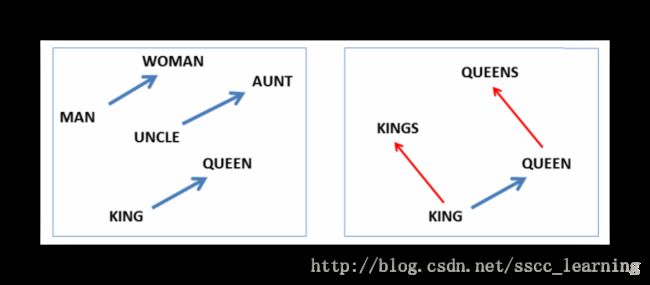
下面是评估公式，找出可以取得最大值的word x x ，就是最有可能对应的结果。

类比可以分成语义上的和语法上的。

首先语义上的，
这种方法存在一些问题：
1. 同一个word在不同句子中可能有不同的意思；
2. 随着时间的改变，word含义有可能会改变。

在语法上，主要是同一个单词的不同形式转换。

Word Correlation 关联

主要是由人标记出来的关系得分，这种方法其实也存在一些模糊不清的可能。

Extrinsic Evaluation 外在

Subsequent Task

之前的评估是直接对word进行的，Extrinsic 是指不直接进行评估，而是通过后面的task看看结果，从而对其进行判断。
这样做有一些优点，首先，可以将两个看似不相干但实际有关联的word联系起来，比如地区名称。还有可以得到words合并后的信息，比如在情感分析方面的应用。

Softmax & Cross-Entropy

Softmax

之前有简单讲过使用softmax进行转换，这里又详细讲解了softmax的定义。
权重 Wy W y 与 x x 相乘后得到 fy f y ，经过 exp e x p 转换成 exp(fy) e x p ( f y ) 。所有的 y y 都经过这种转换后求和，最后将每个 exp(fy) e x p ( f y ) 除以总和得到最终的结果。

softmax的损失函数整理后会得到如下两项，第一项为 −fi − f i ，第二项为 log∑jexp(fj) l o g ∑ j e x p ( f j ) 。
真实结果是 fi f i ，当预测结果 fj f j 不正确时， fi f i 此时会小于 第二项。我们的目的是使得 C(θ) C ( θ ) 最小，所以会不断地优化，直到找出结果正确时的参数。

Cross-Entropy 交叉熵

目标与预测结果的概率分布还可以用交叉熵来表示。其中 p p 就是one-hot-encode表示的target word，而 q q 是预测的概率分布。如果 H(p,q) H ( p , q ) 结果越大，说明两者差异越大；反之，结果越小，说明差异越小。

使用KL-divergence 将公式进行转换。

下面讲解了，实际上这两种loss本质上是一样的。

总结