GIS可视化—热力图制作与热点分析(二)

本博客知识来源：城市数据派公众号，WeChat ID：udparty。讲师：张海平老师（高级城市数据分析师），本文对讲解PPT中的内容进行总结概括，并方便自己以及他人更加直观的了解与学习热力图方面的知识。
　　声明：未经博主允许请勿转载；博主汇总知识仅为学习，如有侵权请联系作者删除博文，谢谢~

相关学习资源（持续更新）

• 空间大数据分析与地图可视化知乎专栏

这篇博客主要介绍对深入的热点模式的探索。

发现要素的关键特征和分布模式

1.从场所到要素的地理对象表达

场所和地图上的点

场所承载了地表的事物和事件，在地图上，大到一个城市，小到一个餐馆、一个宾馆酒店、一个ATM机，甚至一个垃圾桶，这些地理实体对象都可以通过点来表示；此外，某个犯罪事件或交通事故事件等，也都可以在地图上表示为一个点。

点具有地理位

点代表着场所或者事件，则必定存在具体的地理位置，地理位置必然存在着差异。这种不同区域的地理位置点的差异性是空间格局存在的必然条件。

点具有空间关系和模式

地域具有差异性，地理学第一定律的存在，才使空间分析具有实际意义。识别地理模式对于理解地理现象是非常重要的。

2.简单的度量地理分布方法

要素的分布

通过地图上的点表示的场所和事件，如何描述它们的空间分布特征。在ArcGIS中，可以通过简单的基于距离的分布度量模型进行分析汇总。例如，点集的中心位置、中心要素、分布方向、聚散程度等。

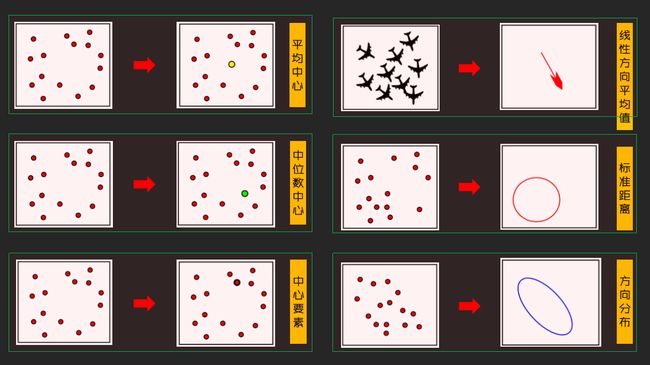
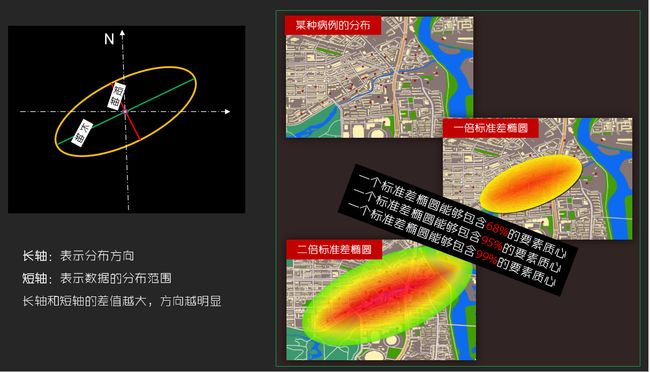
标准差椭圆

通过地图上的点表示的场所和事件，如何描述它们的空间分布特征。在ArcGIS中，可以通过简单的基于距离的分布度量模型进行分析汇总。例如，点集的中心位置、中心要素、分布方向、聚散程度等。

### 3.热点分析理论基础 #### 统计学与数学 　　统计学以数学中的概率论为基础，**自己编一把尺，然后丈量世界，世界他永远看不到尽头，了解的永远只是世界的镜像**。 　　数学是科学的语言，是一门基础学科。其中纯数学研究数量、结构、变化等，以集合论为基础，更多侧重于逻辑演化。**有点“自编自导自演”，世界就在自己手中又何必去追寻世界**；

空间统计与传统统计学

空间统计和非空间统计（传统统计方法）在概念和目标方面可能存在某些相似性，但空间统计具有其固有的独特性，因为它们是专门为处理地理数据而开发的。与传统的非空间统计分析方法不同，空间统计方法是将地理空间（邻域、区域、连通性和/或其他空间关系）直接融入到数学逻辑中。

空间统计与GIS

GIS是地理的语言，计量地理学支撑了地理学作为一门自然科学而存在。GIS的发展，使计量地理模型逐步融入其中，变成了GIS中的各类分析模型和工具。

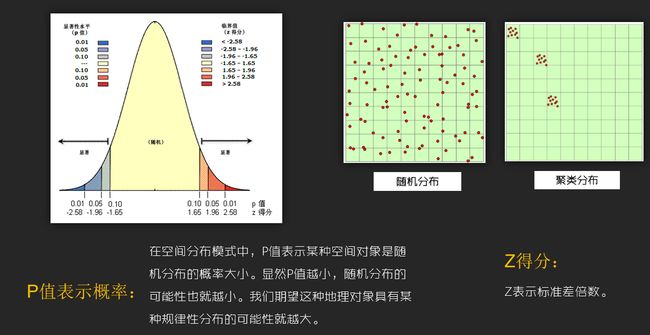
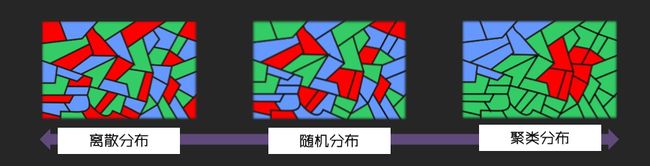
零假设与随机分布

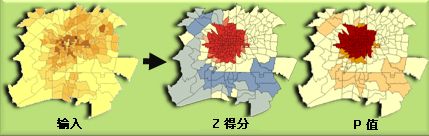
大多数统计检验在开始时都首先确定一个零假设。在空间统计分析中，零假设就是假定某种对象在空间上的分布是随机的。通常通过Z值和P值来进行度量某种对象的空间分布是随机过程还是非随机过程（离散或聚集）。 我们通常希望某种对象的空间模式是聚集的或离散的，而不是随机过程，因此，我们总是希望推翻零假设。

### 4.空间分布模式理论与应用 #### 全局空间分布模式 　　通常情况下，通过地图，我们可以直接通过可视化判断某种地理对象的空间分布模式。然而，如果是同一组对象在不同时间存在细微变化的分布模式，或者具有负责的难以识别的分布模式，就必须通过定量的方法进行分析和描述。 　　另一方面，如下图所示，如果从全局看，显示是聚类的，但如果仅仅将西北角作为研究单元，可能就不是聚类模式了。因此，探索某种对象的空间模式，采用不同的研究单元，得出的结果也可能完全不同。 #### ArcGIS中的全局空间分布模式  平均最邻近（Average Nearest Neighbor ）  空间自相关（Global Moran's I）  增量空间最相关（Incremental Spatial Autocorrelation ）  高低聚类（Getis-Ord General G）  多距离空间聚类分析（Ripley's K Function）

• 平均最邻近（ Average Nearest Neighbor ）：
  　　根据每个要素与其最近邻要素之间的平均距离计算其最近邻指数。其中，临近指数小于1，则表示的模式为聚类， 大于1则表示的模式为趋于离散。

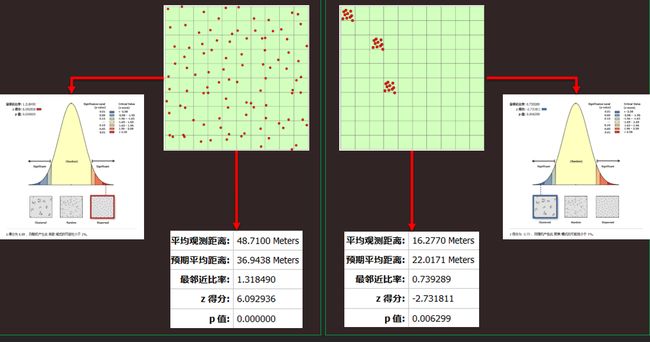
• 空间自相关（ Average Nearest Neighbor ）：
  根据要素位置和属性值使用 Global Moran’s I 统计量测量空间自相关性。

1. **当p值不具有统计学上的显著性** ：不能拒绝零假设。要素值的空间分布很有可能是随机空间过程的结果。观测到的要素值空间模式可能只是完全空间随机性 (CSR) 的众多结果之一。 2. **当p值具有统计学上的显著性** ：其 Z值大于0 可以拒绝零假设。如果基础空间过程是随机的，则数据集中高值和/或低值的空间分布在空间上聚类的程度要高于预期。 3. **当p值具有统计学上的显著性，且 Z值小于0** ：可以拒绝零假设。如果基础空间过程是随机的，则数据集中高值和低值的空间分布在空间上离散的程度要高于预期。离散空间模式通常会反映某种类型的竞争过程 - 具有高值的要素排斥具有高值的其他要素；类似地，具有低值的要素排斥具有低值的其他要素。

空间自相关不仅可以分析点，还可以分析线和面。线和面取要素的中心点进行分析。 另外，以人口为例，采用行政区划面和行政区划点分析的结果不一致。如下所示：

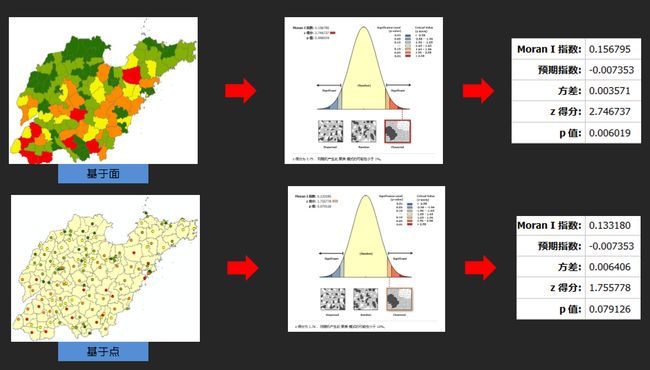
• 高低值聚类（ Getis-Ord General G）：
  使用 Getis-Ord General G 统计可度量高值或低值的聚类程度。

1. **当p值不具有统计学上的显著性** ：不能拒绝零假设。要素值的空间分布很有可能是随机空间过程的结果。观测到的要素值空间模式可能只是完全空间随机性 (CSR) 的众多结果之一。 2. **当p值具有统计学上的显著性** ：可以拒绝零假设。如果基础空间过程是完全随机的，则数据集中高值的空间分布与预期的空间分布相比在空间上的聚类程度更高。 3. **当p值具有统计学上的显著性，且 Z值小于0** ：可以拒绝零假设。如果基础空间过程是完全随机的，则数据集中低值的空间分布与预期的空间分布相比在空间上的聚类程度更高。

5.空间分布模式理论与应用

要素的空间分布特征

1. 总体特征的分析属于二阶效应，几乎都是基于离散点之间的距离实现。
2. 总体特征的分析将传统的平均值，中位数，标准差等推广到地理空间中的要素的分布。

要素的空间分布全局模式

1. ArcGIS提供的要素空间模式分析模型，可以对点、线、面和多点要素进行分析。
2. 此类模型仅仅描述空间要素的全局模式而非局部模式。
3. 有些全局模式分析模型仅仅基于要素的空间位置进行分析，如平均最邻近分析；有些全局模式分析模型则可以基于要素的某个属性值进行分析，如空间自相关和高低值聚类分析。

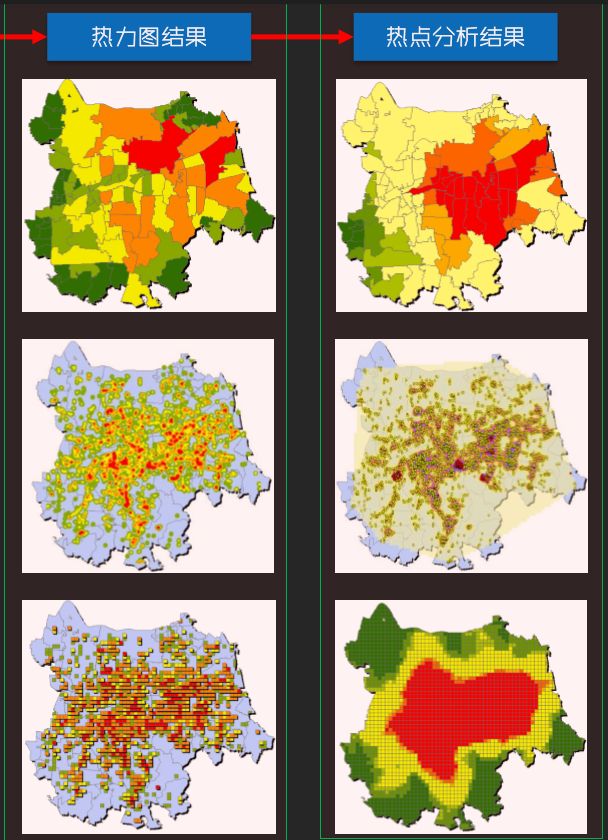
热力图与热点图

1.力图和热点分析的区别

热力图

采用样方统计或者核 密度的方式，对点数 据的全局空间模式进 行分析和表达。是众多聚类方法中的一类，这类分析方法通常通过观察进行模式识别，不能算作是真正意义上的定量分析。

热点分析

尽管可以通过对要素制图来了解它们的总体模式及其关联值，但通过计算统计数据能够将模式量化。对于一些要素，在观察这些要素的过程中，高值要素往往容易引起注意，但可能不是具有显著统计学意义的热点。要成为具有显著统计需意义的热点，要素应具有高值，且被其他同样具有高值的要素所包围通过执行聚类分析来识别具有统计显著性的热点、冷点和空间异常值的位置。查看邻近要素环境中的每一个要素。这种定量模式的发现和可视化，称为热点分析。

　　如上图所示将该地区进行热力图分析和热点分析的结果为： ### 2.聚类分布制图的分析方法 #### 热点分析（ Average Nearest Neighbor ） 　　给定一组加权要素，使用 Getis-Ord Gi* 统计识别具有统计显著性的热点和冷点。 　　局部空间自相关不同于全局空间自相关。它通过计算局部某个要素及其周围要素值的总和与所有要素值的总和进行比较（我们的假设是所有要素是随机分布的，因此任何局部区域的要素值总和值的分布模式和总体的分布模式是一致的）， 当局部实际值和基于全局的预测值不一致时，则拒绝原假设。即具有统计学上的显著性。通过Z得分来描述是热点分布还是冷点分布。 　　注：热点分析一般不会直接通过点数据进行分析，如果分析所用的数据为点，则可以 通过收集事件、构建渔网或者通过行政区划等面要素，空间连接属性后进行分析和制图。

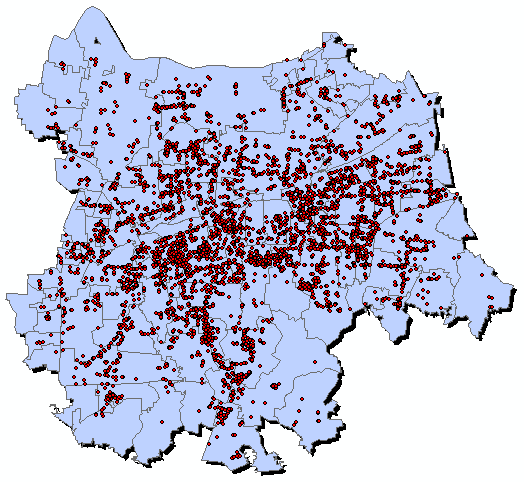
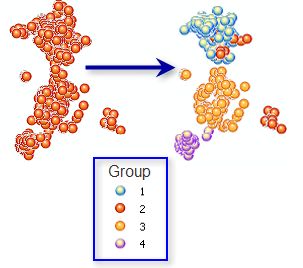
分组分析（ Average Nearest Neighbor ）

根据要素属性和可选的空间/时态约束对要素进行分组。
　　“人以群分，物以类聚”，我们在认识世界上的任何对象时，都会对其进行分类。对于一个明确的分类标准，可以很容易对目标对象进行分类。如对于一个班级的学生，按照性别可以分为男生和女生。但更多的时候，对某个群体的分类并没有一个明确的标准，需要依据一个或多个属性进行自动分类。我们把这类问题叫NP难题。采用分组 分析，可以对数据进行探索性分类。

　　注：在对目标对象进行分类之前，首先需要对数据进行探索性分析，了解数据的特点， 只有这样，才能更加科学的使用此工具，从而得好的分析结果。

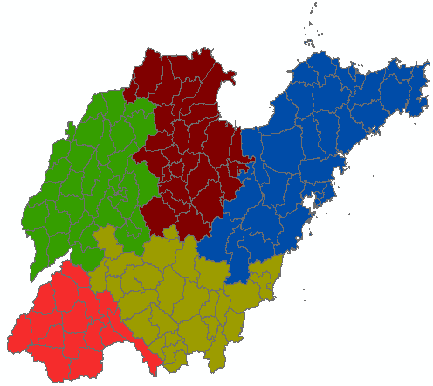
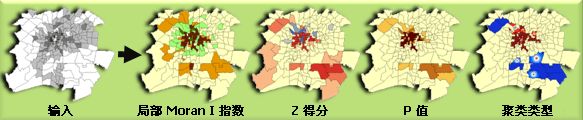
聚类与异常值分析（ Anselin Local Moran’s I ）

给定一组加权要素，使用 Anselin Local Moran’s I 统计量来识别具有统计显著性的热点、冷点和空间异常值。