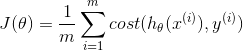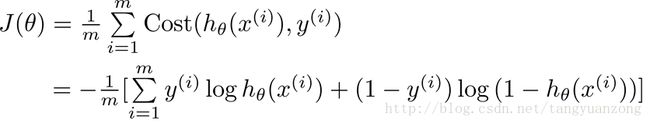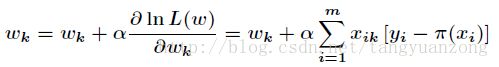实验二 逻辑斯蒂回归
代码地址:github地址
题目:
应用逻辑回归模型预测某学生能否被大学录取。假设你是某大学的系主任,你想根据两次考试的结果决定每个申请者的录取机会。现有以往申请者的历史数据,可以此作为训练集建立逻辑回归模型进行预测。(请按要求完成实验。建议使用python 编程实现。)
数据集:
文件ex2data1.txt 为该实验的数据集,第一列、第二列分别表示申请者两次
考试的成绩,第三列表示录取结果(1 表示录取,0 表示不录取)。
步骤与要求:
1)请导入数据并进行数据可视化,观察数据分布特征。(建议用python 的matplotlib)
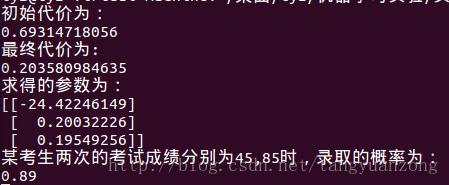
2)将逻辑回归参数初始化为0,然后计算代价函数(cost function)并求出初始值。
3)选择一种优化方法求解逻辑回归参数。
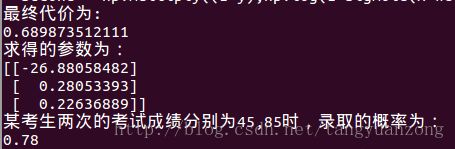
4)某学生两次考试成绩分别为45、85,预测其被录取的概率。
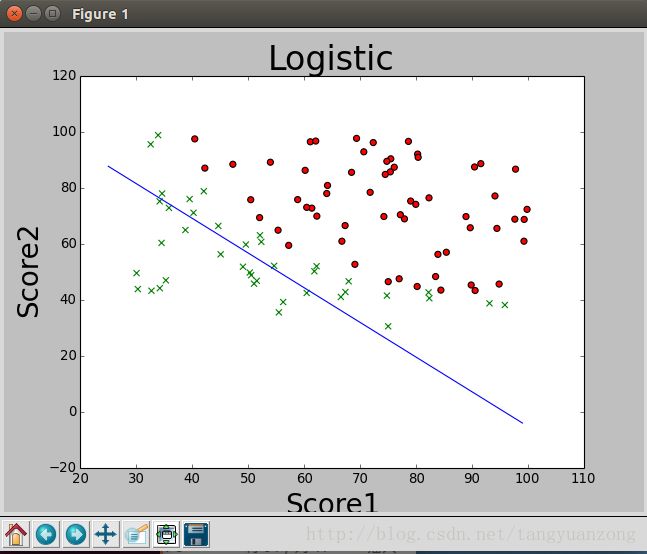
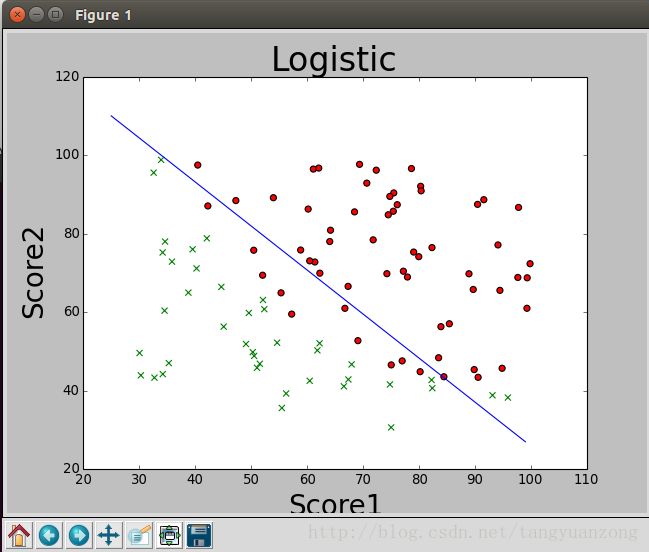
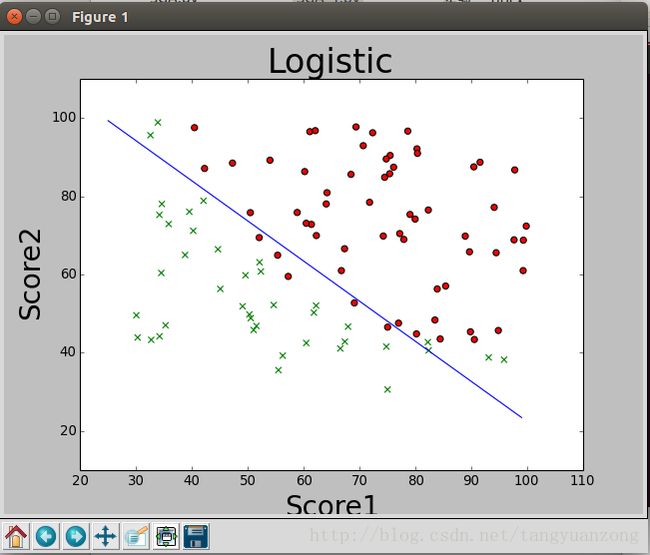
5)画出分类边界。
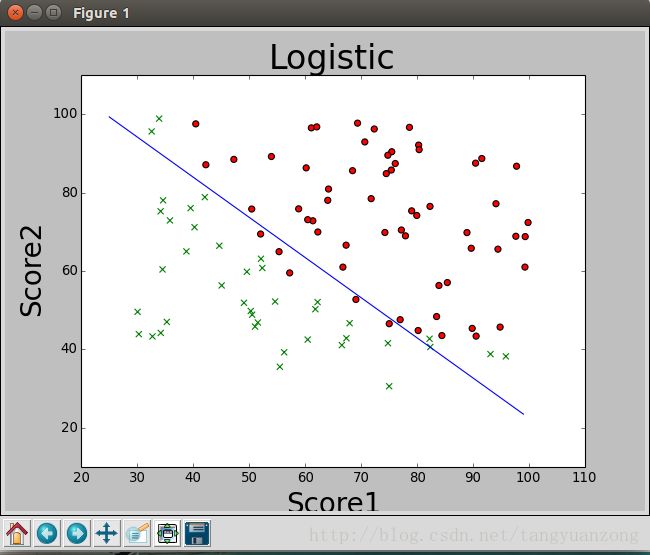
数据可视化:
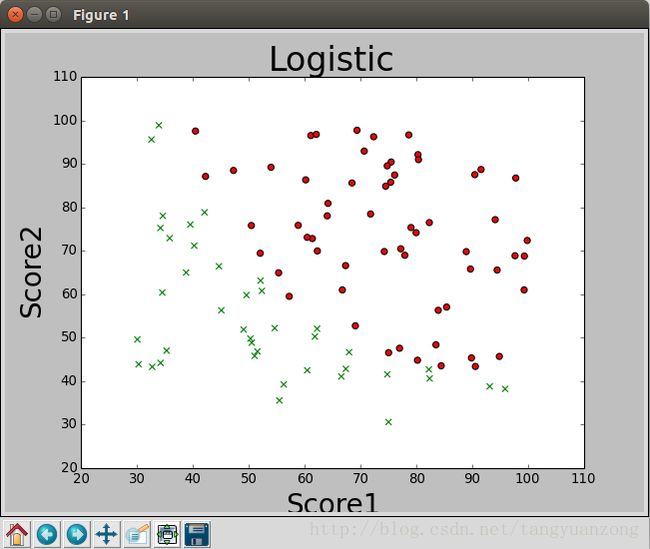
x坐标为学生的第一次成绩,y坐标为学生第二次成绩 ,红色的点表示学生被录取,绿色的x表示未被录取。通过上面的图,我们可以发现,数据是可以被线性可分的。因此可以应用logistic算法对数据进行二分类。
Logistic回归算法:
Logistic回归模型
考虑具有个独立变量的向量
![]() ,
,
设条件慨率为根据观测量相对于某事件发生的概率。那么Logistic回归模型可以表示为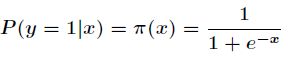 。
。
其中![]()
那么在x条件下y不发生的概率为
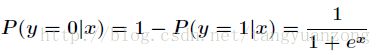
极大似然估计
可以看出Logistic回归都是围绕一个Logistic函数来展开的。接下来就讲如何用极大似然估计求分类器的参数。
假设有m个观测样本,观测值分别为
![]()
设
![]()
为给定条件下得到 ![]() 的概率,
的概率,
同样地![]() ,的概率为
,的概率为![]() ,
,
所以得到一个观测值的概率为![]()
因为各个观测样本之间相互独立,那么它们的联合分布为各边缘分布的乘积。得到似然函数为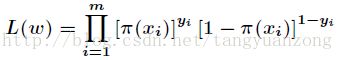
然后我们的目标是求出使这一似然函数的值最大的参数估计,对函数取对数得到: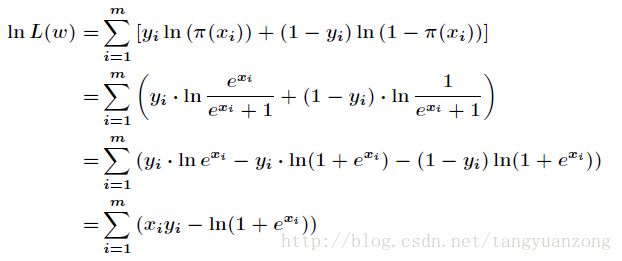
现在求向量![]() ,使得
,使得![]() 最大,其中
最大,其中![]()
代价函数
代码实现:
def cost(weight,x,y):
weight = np.matrix(weight)
x = np.matrix(x)
y = np.matrix(y)
first = np.multiply(-y,np.log(sigmoid(x*weight)))
second = np.multiply((1-y),np.log(1-sigmoid(x*weight)))
return np.sum((first-second)/len(x))求出初始代价:
录取概率预测:
def prdict(weight,x,y):
l =len(x)
c = 0
for i in range(l):
u = x[i][0]*weight[0][0]+x[i][1]*weight[1][0]+x[i][2]*weight[2][0]
u = float(sigmoid(u))
if (y[i]==1 and u >0.5 ) or (y[i]==0 and u <0.5 ):
c+=1
return float(c)/float(l)问题求解方法:
方法一:批量梯度上升法
参数更新公式:
算法框架:
for k in range(maxCycles):
h = sigmoid(xArr*weights) //计算预测值
error = (yArr - h) //真实值与预测值的差值
weights +=alpha * xArr.transpose()*error/100 //在原来的基础上除以100,是为了避免数值过大
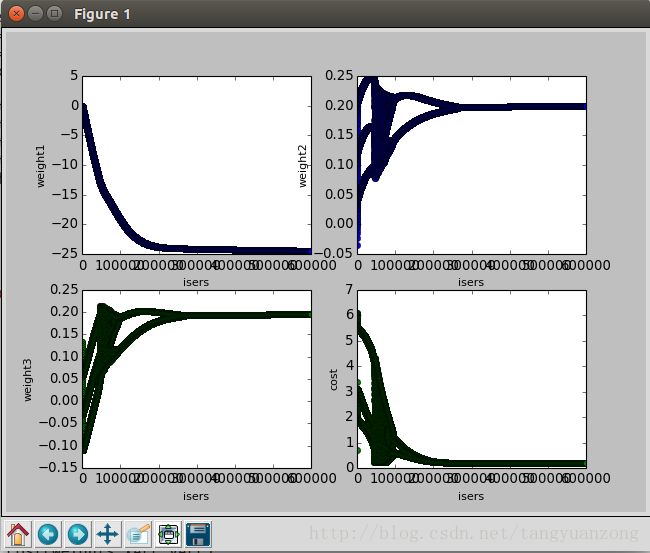
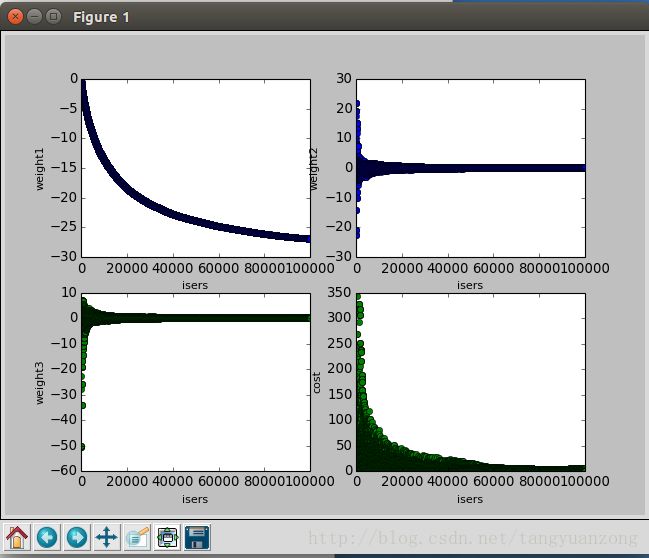
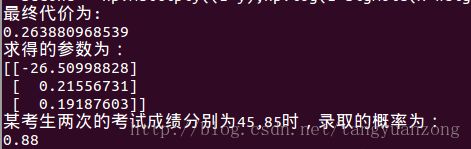
return weights实验结果: α设置为0.004 迭代600000次
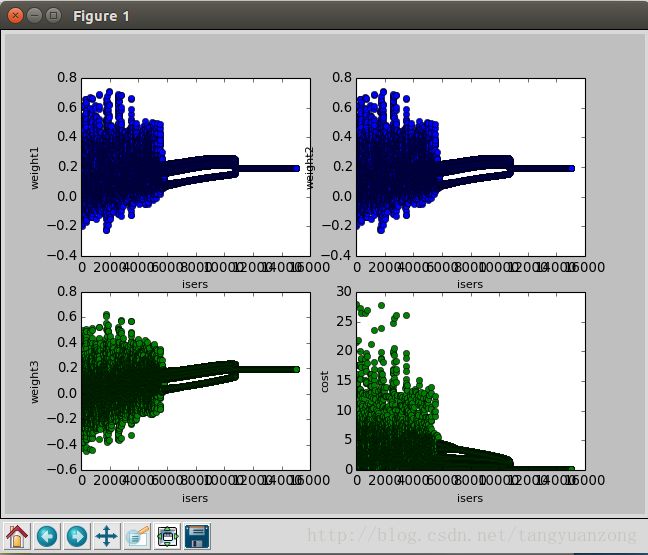
参数变化曲线
最优参数与录取概率:
结果分析:
为了避免数值溢出,我将α设置为0.004,所以在经过60万次迭代之后,才得到了一个最优解。从图像可以看出,大概在迭代30万次的时候,就已经收敛了。但是为了得到更小的代价,我们可以迭代更多的次数。
因为每一次迭代的时候,都需要计算整个数据集的梯度,所以整个过程是非常耗时的。我们还乐意发现,在迭代的前期,参数未收敛,产生剧烈的抖动。这种方法虽然可以得到最优解。但是对于小数据,还可以。当面对海量数据时,就非常耗时了。
方法二:随机梯度上升法
批量梯度上升算法在每次更新权值向量的时候都需要遍历整个数据集,该方法对小数据集尚可。但如果有数十亿样本和成千上万的特征时,它的计算复杂度就太高了。一种改进的方法是一次仅用一个样本点的回归误差来更新权值向量,这个方法叫随机梯度上升算法。由于可以在遇到新样本的时候再对分类器进行增量式更新,所以随机梯度上升算法是一个在线学习算法;与此对应,一次处理完所有数据的算法(如梯度上升算法)被称作“批处理”。同时,为了让参数收敛,我们可以不断的减少α的值。
算法框架:
for k in range(maxCycles): //迭代次数
for j in range(m): //遍历数据集
alpha = 1.3/(1.0+k+j)+0.0002 //不断减小α的值
h = sigmoid(sum(xArr[j]*weights)) //计算预测值
error = yArr[j] - h //计算差值
weights += alpha * xArr[j].transpose()*error //更新参数
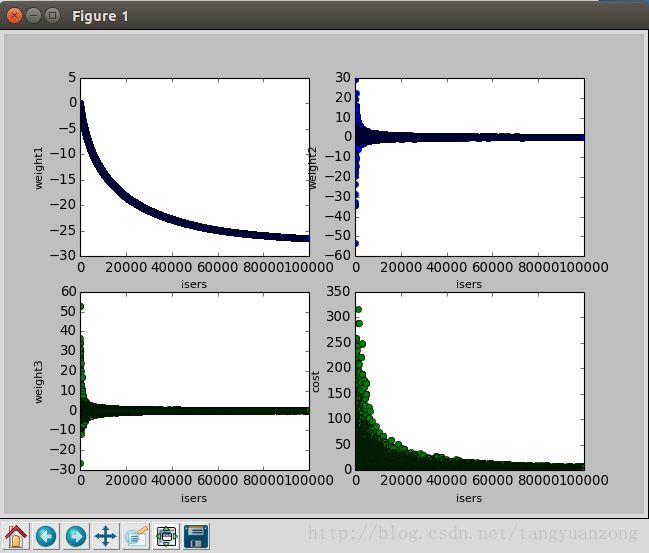
return weights实验结果: 迭代1000次
参数变化曲线:
最优参数与录取概率:
结果分析:
我们发现,最后得到正确率并没有批量梯度上升算法的那么高,但是在迭代的过程中,参数不会产生剧烈的抖动,并且参数可以很快的收敛。
方法三:改进的随机梯度上升法
上面的算法,虽然叫做随机梯度上升算法,但是并不是真正意义上的随机梯度上升,它只是每次迭代的时候,顺序的选择数据。因此,我们可以得到一种,真正意义上的随机梯度上升算法:每次迭代时,随机的选择数据,而不是顺序的选择数据。
算法框架:
for k in range(maxCycles): //迭代次数
dataidex = range(m)
for j in range(m): //遍历数据集
alpha = 1.3/(1.0+k+j)+0.0002 //减少阿尔法
randidex = int(random.uniform(0,len(dataidex))) //随机选择某个数据
h = sigmoid(sum(xArr[randidex]*weights)) //计算预测值
error = yArr[randidex] - h //计算差值
weights += alpha * xArr[randidex].transpose()*error //更新参数
del(dataidex[randidex]) //删除被选择的数据下标
return weights实验结果:迭代1000次
参数变化曲线:
最优参数与录取概率:
结果分析:
我们发现,同样的α,同样的迭代次数。真正的随机上升算法所得到的cost与之前批量梯度下降所得到的cost非常接近,但是迭代次数,却减少很多。
方法四:动量法
从本质上说,动量法,就仿佛我们从高坡上推下一个球,小球在向下滚动的过程中积累了动量,在途中他变得越来越快(直到它达到了峰值速度,如果有空气阻力的话,γ<1)。在我们的算法中,相同的事情发生在我们的参数更新上:动量项在梯度指向方向相同的方向逐渐增大,对梯度指向改变的方向逐渐减小。由此,我们得到了更快的收敛速度以及减弱的震荡。
公式:
算法框架:
for k in range(maxCycles): //迭代次数
h = sigmoid(xArr*weights) //计算预测值
error = (yArr - h) //计算差值
v = gama * v + alpha * xArr.transpose()*error/100 //更新v值
weights += v //更新参数
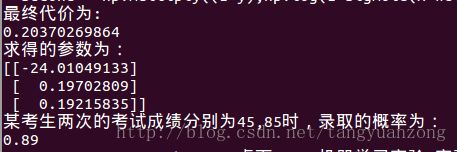
return weights实验结果:迭代15000次 α=0.004
参数变化曲线:
最优参数与录取概率:
结果分析:
同样的α,使用动量法求解的结果和批量梯度上升法求解的结果非常接近。但是动量法却只迭代了15000次。但是动量法,有个问题就是没收敛之前,参数波动太大。