【算法导论】图的广度优先搜索遍历（BFS）

       图的存储方法：邻接矩阵、邻接表

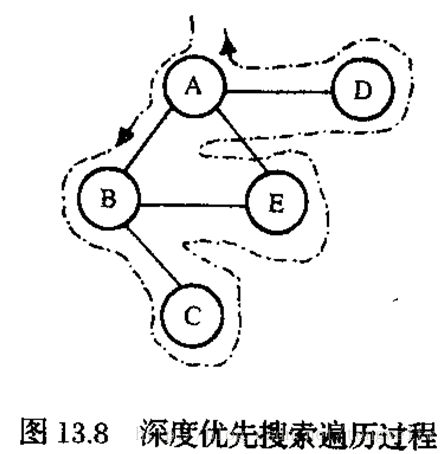
       例如：有一个图如下所示(该图也作为程序的实例)：

则上图用邻接矩阵可以表示为：

用邻接表可以表示如下：

邻接矩阵可以很容易的用二维数组表示，下面主要看看怎样构成邻接表：

        邻接表存储方法是一种顺序存储与链式存储相结合的存储方法。在这种方法中，只考虑非零元素，所以在图中的顶点很多而边很少时，可以节省存储空间。
        邻接表存储结构由两部分组成：对于每个顶点vi, 使用一个具有两个域的结构体数组来存储，这个数组称为顶点表。其中一个域称为顶点域(vertex)，用来存放顶点本身的数据信息；而另一个域称为指针域(link)，用来存放依附于该顶点的边所组成的单链表的表头结点的存储位置。邻接于vi的顶点vj链接成的单链表称为vi的邻接链表。邻接链表中的每个结点由两个域构成：一是邻接点域(adjvex)，用来存放与vi相邻接的顶点vj的序号j (可以是顶点vj在顶点表中所占数组单元的下标)； 其二是链域(next)，用来将邻接链表中的结点链接在一起。具体的程序实现如下：

void CreateAdjTable(vexnode ga[N],int e)//创建邻接表
{
	int i,j,k;
	edgenode *s;
	printf("\n输入顶点的内容：");
	for(i=0;iadjvex=j;
		s->next=ga[i].link;
		ga[i].link=s;

		s=(edgenode *)malloc(sizeof(edgenode));
		s->adjvex=i;
		s->next=ga[j].link;
		ga[j].link=s;

	}
}

广度优先搜索遍历（BFS）:

        图的广度优先搜索遍历类似于树的按层次遍历。在假设初始状态是图中所有顶点都未被访问的条件下，这种方法从图中某一顶点vi出发，先访问vi，然后访问vi的邻接点vj。在所有的vj都被访问之后，再访问vj的邻接点vk，依次类推，直到图中所有和初始出发点vi有路径相通的顶点都被访问为止。若图是非连通的，则选择一个未曾被访问的顶点作为起始点，重复以上过程，直到图中所有顶点都被访问为止。 
        在这种方法的遍历过程中，先被访问的顶点，其邻接点也先被访问，具有先进先出的特性，所以可以使用一个队列来保存已访问过的顶点，以确定对访问过的顶点的邻接点的访问次序。为了避免重复访问一个顶点，也使用了一个辅助数组visited[n]来标记顶点的访问情况。下面分别给出以邻接矩阵和邻接表为存储结构时的广度优先搜索遍历算法BFS_matrix和BFS_AdjTable:

具体程序实现如下：

#include
#include
#define N 5

//邻接矩阵存储法
typedef struct 
{
	char vexs[N];//顶点数组
	int arcs[N][N];
}graph;

//邻接表存储法
typedef struct Node
{
	int adjvex;
	struct Node *next;

}edgenode;

typedef struct
{
	char vertex;
	edgenode *link;
}vexnode;

//队列操作
typedef struct node
{
	int data;
	struct node *next;
}linklist;

typedef struct
{
	linklist *front,*rear;
}linkqueue;

void SetNull(linkqueue *q)//队列置空
{
	q->front=(linklist *)malloc(sizeof(linklist));
	q->front->next=NULL;
	q->rear=q->front;
}

int Empty(linkqueue *q)
{
	if(q->front==q->rear)
		return 1;
	else 
		return 0;
}

int Front(linkqueue *q)//取队头元素
{
	if(Empty(q))
	{
		printf("queue is empty!");
		return -1;
	}
	else
		return q->front->next->data;
}

void ENqueue(linkqueue *q,int x)//入队
{
	linklist * newnode=(linklist *)malloc(sizeof(linklist));
    q->rear->next=newnode;
	q->rear=newnode;
	q->rear->data=x;
	q->rear->next=NULL;
	
}

int DEqueue(linkqueue *q)//出队
{
	int temp;
	linklist *s;
	if(Empty(q))
	{
		printf("queue is empty!");
		return -1;
	}
	else
	{
		s=q->front->next;
		if(s->next==NULL)
		{
			q->front->next=NULL;
			q->rear=q->front;
		}
		else
			q->front->next=s->next;
		temp=s->data;
		return temp;
	}
}

void BFS_matrix(graph g,int k,int visited[N])//图按照邻接矩阵存储时的广度优先遍历
{
	int i=0;
	linkqueue q;
	SetNull(&q);
	printf("%c\n",g.vexs[k]);
	visited[k]=1;
	ENqueue(&q,k);
	while(!Empty(&q))
	{
		i=DEqueue(&q);
		for(int j=0;jadjvex=j;
		s->next=ga[i].link;
		ga[i].link=s;

		s=(edgenode *)malloc(sizeof(edgenode));
		s->adjvex=i;
		s->next=ga[j].link;
		ga[j].link=s;

	}
}

void BFS_AdjTable(vexnode ga[],int k,int visited[N])//图按照邻接表存储时的广度优先遍历
{
	int i=0;
	edgenode *p;
	linkqueue q;
	SetNull(&q);
	printf("%c\n",ga[k].vertex);
	visited[k]=1;//标记是否被访问过
	ENqueue(&q,k);//入队
	while(!Empty(&q))
	{
		i=DEqueue(&q);
		p=ga[i].link;
		while(p!=NULL)
		{
			if(visited[p->adjvex]!=1)
			{
				printf("%c\n",ga[p->adjvex].vertex);
				visited[p->adjvex]=1;
				ENqueue(&q,p->adjvex);
			}
			p=p->next;
		}
	}
}


void main()
{
	graph g;
	vexnode ga[N];
	int visited[5]={0};
	int visited1[5]={0};
	g.vexs[0]='A';
	g.vexs[1]='B';
	g.vexs[2]='C';
	g.vexs[3]='D';
	g.vexs[4]='E';
	int a[5][5]={{0,1,0,1,1},{ 1,0,1,0,1},{ 0,1,0,0,0},{ 1,0,0,0,0},{ 1,1,0,0,0}};
	for(int i=0;i<5;i++)
		for(int j=0;j<5;j++)
			g.arcs[i][j]=a[i][j];
	printf("图按照邻接矩阵存储时的广度优先遍历：\n");
	BFS_matrix(g,0,visited);
	CreateAdjTable(ga,5);
	printf("图按照邻接表存储时的广度优先遍历：\n");
	BFS_AdjTable(ga,0,visited1);
}

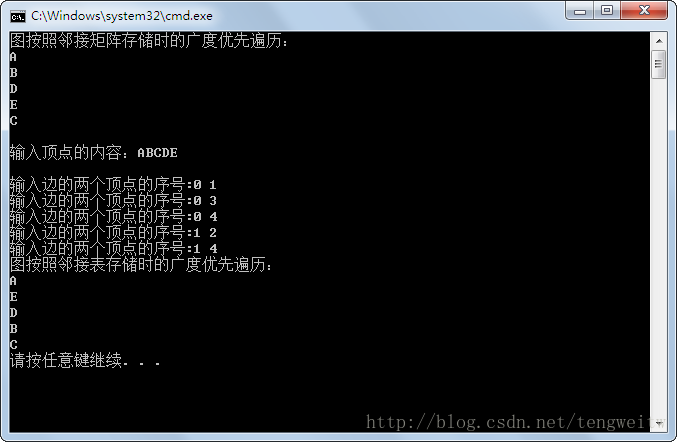
其结果如下图：

从上面可以看出，两种方式的结果不同，但都是正确的，因为这与邻接点访问的顺序有关。

注：如果程序出错，可能是使用的开发平台版本不同，请点击如下链接： 解释说明

原文：http://blog.csdn.net/tengweitw/article/details/17228937

作者：nineheadedbird