Java方法的嵌套与递归调用

写在前面：博主是一只经过实战开发历练后投身培训事业的“小山猪”，昵称取自动画片《狮子王》中的“彭彭”，总是以乐观、积极的心态对待周边的事物。本人的技术路线从Java全栈工程师一路奔向大数据开发、数据挖掘领域，如今终有小成，愿将昔日所获与大家交流一二，希望对学习路上的你有所助益。同时，博主也想通过此次尝试打造一个完善的技术图书馆，任何与文章技术点有关的异常、错误、注意事项均会在末尾列出，欢迎大家通过各种方式提供素材。

• 对于文章中出现的任何错误请大家批评指出，一定及时修改。
• 有任何想要讨论和学习的问题可联系我：[email protected]。
• 发布文章的风格因专栏而异，均自成体系，不足之处请大家指正。

Java方法的嵌套与递归调用

本文关键字：方法、嵌套、递归、经典问题

一、方法的嵌套

1. 概念解读

方法嵌套的概念其实比较好理解，就是在调用方法的过程中又遇到了方法的调用，在刚开始接触的时候虽然在逻辑上能够理解为什么运行结果是这样的，但是对于代码执行的过程还是感觉有些绕。

2. 方法嵌套

在编程中最常见的就是方法与方法之间的调用嵌套，因为通常情况下，我们解决一个问题不会只靠一个方法。而且如果一个方法所提供的功能十分强大，那势必其中的代码逻辑和参数列表也会变的相对复杂，不利于修改和使用，所以我们希望，每个方法都是一个个小小的利刃，用来解决特定的问题，通过组合使用的方式来完成一个较为复杂的功能，就像雷恩的七星刀一样。

比如，我们已经有了两个方法：分别用于计算圆的面积和计算矩形的面积，如果我们现在需要算一个圆柱的表面积，我们还需要把整个方法重写一遍吗？当然不需要，因为圆柱的表面积的计算刚好可以通过两个圆柱底面积（圆）加圆柱侧面积（矩形）得到，我们只需要合理的传入参数和进行值的返回即可实现。

public class Test{
    public static void main(String[] args){
        // 计算一个圆柱的面积，已知底面半径和高
        int radius = 5;
        int height = 10;
        // 调用计算圆柱表面积
        double area = getColumnArea(radius,height);
        // 输出结果
        System.out.println("圆柱的表面积为：" + area);
    }
    public static double getCircleArea(double radius){
        // 根据圆的半径计算面积后返回
        return Math.PI * Math.pow(radius,2);
    }
    public static double getRectangleArea(double width,double height){
        // 根据宽和高计算面积后返回
        return width * height;
    }
    public static double getColumnArea(double radius,double height){
        // 计算得到底面积 -> 刚好是侧面积的宽
        double baseArea = getCircleArea(radius);
        // 计算得到侧面积
        double lateralArea = getRectangleArea(baseArea,height);
        // 根据底面积及侧面积计算后返回
        return baseArea * 2 + lateralArea;
    }
}

那么，整个方法的执行过程是怎样的呢？其实依然是个顺序结构，当一个被调用的方法完全执行后才会继续进行后续的步骤，我们可以将这个过程描述如下：

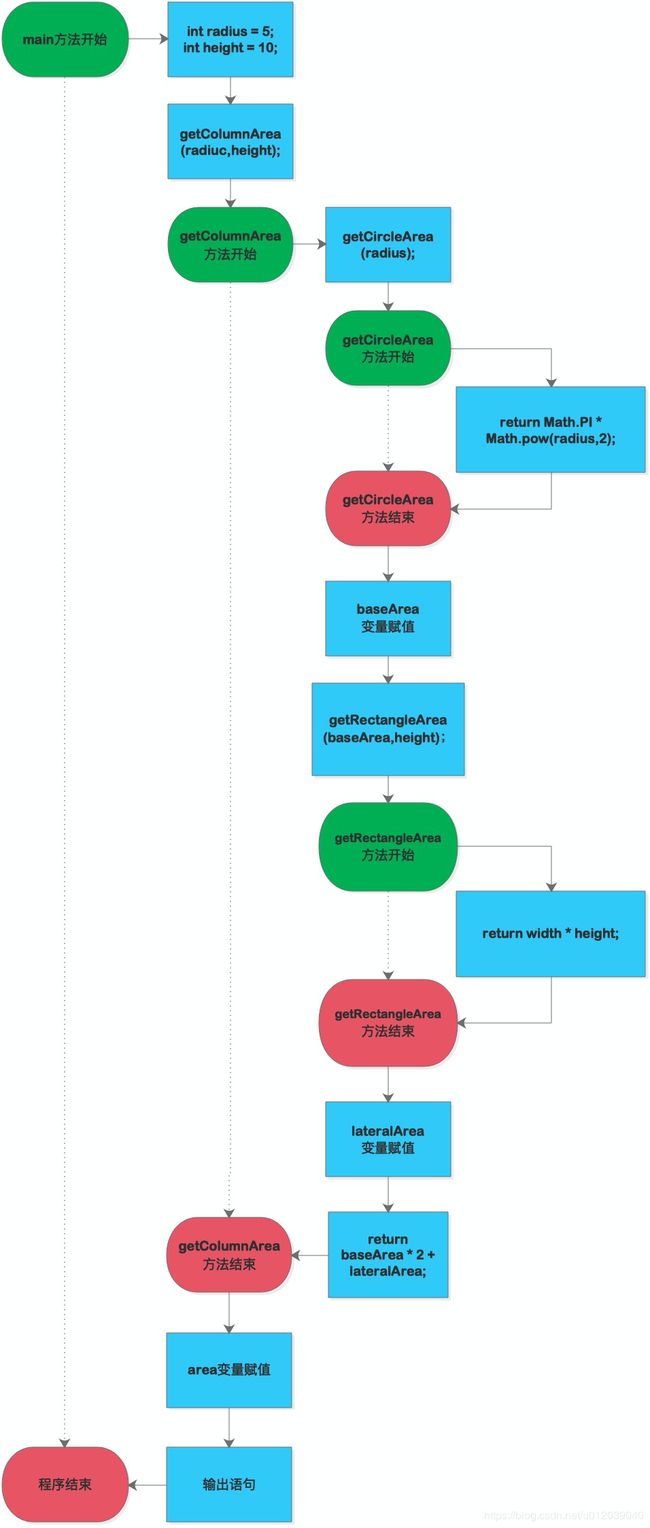
3. 构造嵌套

在之前的文章中已经向大家介绍了构造器的重载，可以适用于对不同个数的属性进行初始化，直击传送门：Java初始化对象的工具 - 构造器。但是在使用时我们会发现一个问题，构造器的主要用途是为属性赋值，但是在构造器重载时会发现，一样有代码的冗余，会出现为很多相同的赋值语句，作为强迫症的重度患者，这是不能忍受的，看下面的例子：

public class Person{
    // 一参构造器
    public Person(String name){
        this.name = name;
    }
    // 两参构造器，可以给name和age属性赋值
    public Person(String name,int age){
        this.name = name;
        this.age = age;
    }
    // 三参构造器，可以给name、age和job属性赋值
    public Person(String name,int age,String job){
        this.name = name;
        this.age = age;
        this.job = job;
    }
    public String name;
    public int age;
    public String job;
}

在上面的例子中一共定义了三个构造器，分别满足不同的初始化需要（当然，我们还可以定义的更多），但是可以发现很多赋值语句都是重复的，我们可以通过构造器互相调用的方式来减少代码量。在当前类中构造器进行相互调用，使用this()的方式来完成，括号中填入相应的参数，修改后代码如下。

public class Person{
    // 一参构造器
    public Person(String name){
        this.name = name;
    }
    // 两参构造器，可以给name和age属性赋值
    public Person(String name,int age){
        this(name);
        this.age = age;
    }
    // 三参构造器，可以给name、age和job属性赋值
    public Person(String name,int age,String job){
        this(name,age);
        this.job = job;
    }
    public String name;
    public int age;
    public String job;
}

假如在测试类中使用三参构造器来初始化一个Person对象：Person person = new Person(“小张”,25,”工程师“);则执行过程如下：

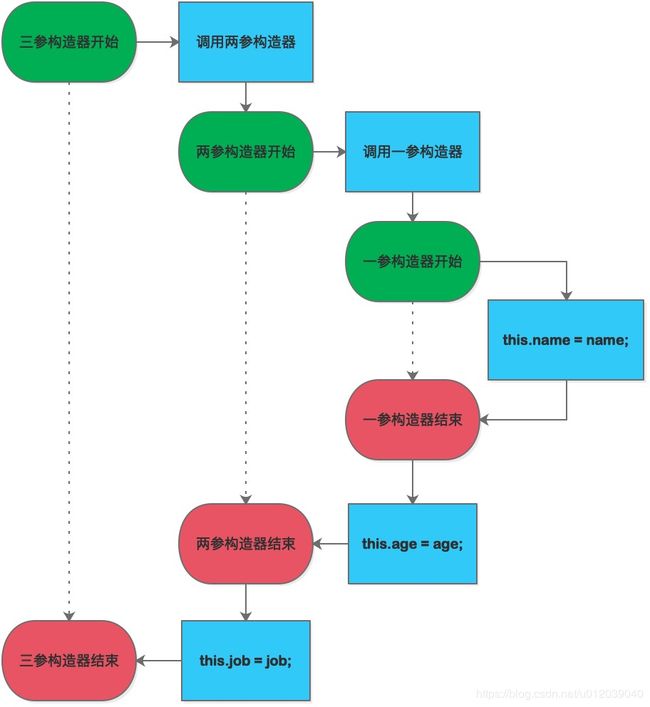
二、方法的递归

1. 概念解读

递归是一种计算过程或方法，是一种将问题分解为同类的子问题来解决问题的方法，那么什么是同类子问题呢？就是对一个大问题进行拆解，而得到的子问题又是同一规则，或同一种操作，比如最简单的阶乘计算。假如我们需要计算4的阶乘，直接用数学的方式写出来是4! = 4 x 3 x 2 x 1。
那么我们如何用计算机解决这个问题呢？当然，我们可以使用循环，从给定的数一直乘到1为止：

public class Test{
    public static void main(String[] args){
        int n = 4;
        int result = 1;
        for(int i = n;i <= 1;i--){
            result *= i;
        }
        System.out.println(result);
    }
}

但是其实这可以总结或者分解为一个规律：n! = n x (n - 1)!，n ≥ 2；n! = 1，n = 1。那这和循环又有什么区别呢？区别在于我们在使用循环时，我们自己将这个计算过程完全翻译成了计算机可以读懂和直接执行的代码，而却没有了原本的意义，并且在某些情况下，并不是所有问题都可以通过循环结构实现。另外一方面，计算理论可以证明递归的作用可以完全取代循环，但是出于性能的考虑，我们也不会刻意的用递归去代替循环，而更偏向于使用递归去解决某一类特定的问题。

2. 递归思想

从上面的介绍中可以看到，我们希望通过递归的思想尽量的贴近原有问题的描述，并能将问题很好的解决。从代码的角度来看，递归方法一句话来概括就是：自己调用自己。为什么这么说呢？因为整个的执行过程都是通过重复一个步骤来实现的，每一步结果的产生都来自于上一步或前一步。那么问题就来了，什么时候是个头呢？这就引出了一个概念：递归的出口。
就像循环需要有一个终止条件一样，递归在不断的调用自己，去获取自己所需要的结果，那同样要有一个终止条件，这个条件的设定通常比较明显，那就是能得到一个确切的结果时，就不需要再进行递归调用了，此时直接将具体结果返回就可以了，比如我们使用递归去实现阶乘：

public class Test{
    public static void main(String[] args){
        int n = 4;
        int result = getFactorial(n);
        System.out.println(result);
    }
    // 定义一个方法，用于计算n的阶乘，不考虑n < 0的情况
    public static int getFactorial(int n){
        // 递归的出口
        // 描述当n = 1时，阶乘的结果为1，直接返回确定的结果
        if(n == 1){
            return 1;
        }else{
            // 根据规律，此时应该先获取到n - 1的阶乘的结果
            // 描述当n ≥ 2时，n! = n x (n - 1)!
            return n * getFactorial(n - 1);
        }
    }
}

当我们整理出一个公式或描述出一个规律之后，我们可以尝试按照如下思路进行思考：

• 首先需要确定递归的出口，也就是判断条件，通常出口即为：能够得到确定值时传入参数的取值
• 接下来就是确定出口的内容，也就是符合判断条件时，得到的确定值
• 最后就是递归调用的部分，根据总结出的规律，用表达式表述出来

3. 执行过程

如果大家理解了这个分解的过程，那么我们已经从代码上实现了这个描述，当n = 1时，直接就可以得到确定的结果：1；当n ≥ 2时，通过递归调用（调用自己），将n - 1作为参数传入，代表想要获取n - 1的递归的值，将n - 1传入后，如果不能得到确定的结果，就会继续调用，那么整体的运算过程可以用下图来表示：

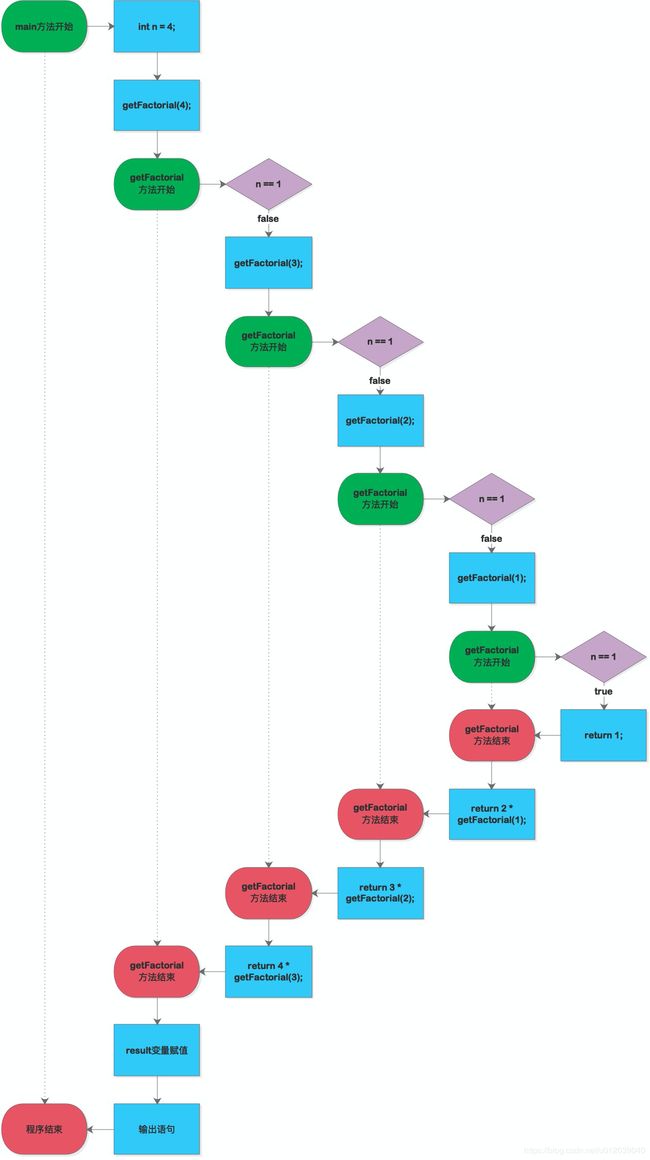
4. 经典问题

• 斐波那契数列

斐波那契数列是一个很经典的数列，第一项为1，第二项为1，从第三项开始，每一项的值都是前两项的和，用数学的方式整理一下就是：当n = 1或n = 2时，f(n) = 1；当n ≥ 3时，f(n) = f(n - 1) + f(n - 2)。按照之前的步骤，我们可以确定出口为n = 1或n = 2，得到的确定值为：1，递归调用的部分即为：f(n - 1) + f(n - 2)，据此写出程序：

public class Test{
    public static void main(String[] args){
        int n = 5;// 自定义一个正整数n
        int result = f(n);
        System.out.println(result);
    }
    public static int f(int n){
        // 递归出口：当n = 1或n = 2时终止调用，得到确定的值
        if(n == 1 || n == 2){
            return 1;
        }else{
            // 自第三项开始，结果为前两项的加和
            return f(n - 1) + f(n - 2);
        }
    }
}

• 杨辉三角

杨辉三角是一个很有趣的图形，一个金字塔的构图，顶部和两侧的值固定为1，此时你应该想到什么？没错，递归出口！其他部分的值为上一层中与它最邻近的两个值的加和，如：自顶向下（第4层，第3列），它的值为（第3层，第2列） + （第3层，第3列）。

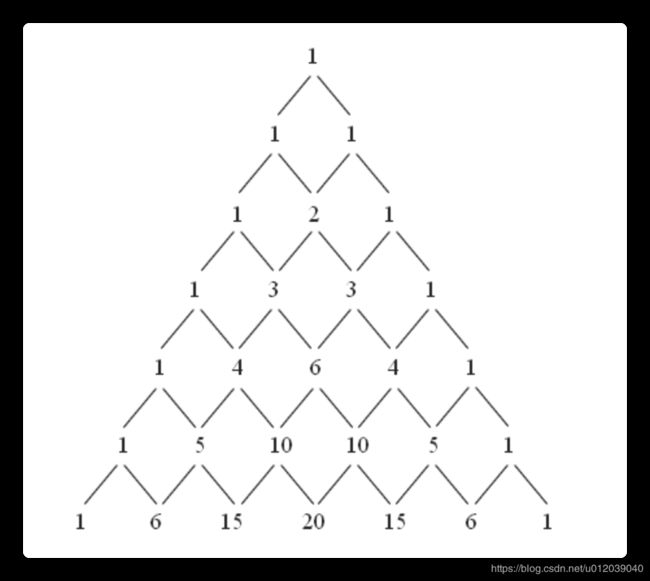
如果我们用变量i代表层，j代表这一层的列，那么（i，j）的值为（i - 1，j - 1） + （i - 1，j），这是什么？没错，规律的描述！最后我们只需要搞定递归出口的判定条件，一切就大功告成啦！由上面的构图我们知道，每一层的元素的个数，不会超过这一层的层数，并且刚好相等，所以你知道顶部和两侧该如何描述了吗？

public class Test{
    public static void main(String[] args){
        int i = 4;// 定义一个正整数i
        int j = 3;// 定义一个正整数j,大小不能超过i
        int result = getN(i,j);
        System.out.println(result);
    }
    public static int getN(int i,int j){
        // 第1层和第1列的值固定为1，最后一列的值也固定为1
        if(i == 1 || j == 1 || j == i){
            return 1;
        }else{
            // 使用表达式描述规律
            return getN(i - 1,j - 1) + getN(i - 1,j);
        }
    }
}

以为这就完了？怎么会！既然碰到了这么美丽的图形，不通过程序打印出来如何能消心头之痒！与获得单个的数值不同，打印时要求输入的是想要显示的层数，那么我们就要用到双重for循环来构建出整个图形了：

public class Test{
    public static void main(String[] args){
        int n = 5;// 定义一个正整数n
        print(n);
    }
    public static void print(int n){
        for(int i = 1;i <= n;i ++){
            // 在每行前插入空格，空格数量与目标层数相关
            for (int j = i;j <= n;j++){
                System.out.print(" ");
            }
            for (int j = 1;j <= i;j++){
                // 输出后进行留空
                System.out.print(getN(i,j) + " ");
            }
            // 打印一层后换行
            System.out.println();
        }
    }
    public static int getN(int i,int j){
        // 第1层和第1列的值固定为1，最后一列的值也固定为1
        if(i == 1 || j == 1 || j == i){
            return 1;
        }else{
            // 使用表达式描述规律
            return getN(i - 1,j - 1) + getN(i - 1,j);
        }
    }
}

运行结果如下：