前序:花了好几天才把带你飞系列的KMP专题(地址:https://vjudge.net/contest/246969#overview搞定,刷了很多题,发现KMP可以用来解决这几类问题:
①单个字符串匹配问题(s1在s2中匹配):这个用strstr(const char* big, const char* small)函数也可以,这个函数返回small在big函数中首次出现的地址,没有出现就返回NULL。区别在于:
1️⃣如果只是求s1是否在s2中出现过的话,建议可以用strstr函数,这个函数的复杂度还是可以接受的(如果数据量达到1e6就还是老老实实用kmp,用这个函数会TLE,例如A题),如果实在不行,再换用kmp模板吧。当然strstr只能适用字符数组,若是数字就直接上kmp吧,当然,强行把数字用字符存也不是不可以,QAQ。
2️⃣如果求s1在s2中出现了几次(分为可重叠与不可重叠),就只能用kmp了。
3️⃣如果求s1在s2首次出现的下标,用kmp可以直接返回下标,而strstr函数貌似也可以,不过由于返回的是地址,需要转化一下。
附上kmp求以上问题的kmp_pre的各种变形
int KMP_Count(char s[], char p[]){
kmp_pre();
cnt = 0;
int i,j;
i = j = 0;
int n = strlen(s);
int m = strlen(p);
while(i < n){
while(j != -1 && s[i] != p[j]) j = nextt[j];
++i; ++j;
if(j >= m){
cnt++; //记录p在s中出现的个数
j = nextt[j]; //p在s中可以覆盖、重叠,例如s=abababa p=aba,最后cnt=3
//j = 0; //p在s中不可以覆盖、重叠,例如s=abababa p=aba,最后cnt=2
//return 1; //返回存在
//return i-m+1; //返回p首次在s中出现的下标
}
}
return cnt; //返回出现次数
//return 0; //返回不存在
// return -1; //p首次在s中出现的下标为-1,表示s中没有p
}
②字符串循环节问题(nextt数组的运用一):感觉kmp最牛的地方就是nextt数组了,nextt数组又称前缀数组(或许叫做最长前后缀数组更加合适),先看张图哈:
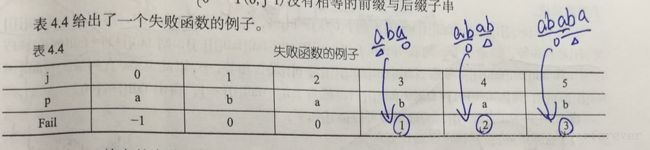
可以看出nextt[i]其实就是字符串s[0~(i-1)]的前后缀的最大相等长度。需要注意的是nextt[0]=-1,nextt[0]=0是不变的,至于原因,结合nextt的定义不难理解。还有就是上图中,其实nextt[6]=4,可以发现4就是字符串ababab的前后缀的最大相等长度,而6(字符串长度)-4=2即为循环节的长度。所以循环节的长度公式为:l = len-nextt[len],其中len为字符串的长度。这里也要分两种情况
1️⃣len%l == 0:就是字符串的长度是循环节的整数倍,有一种比较特殊的情况就是l == len这种类型的伪循环,例如abcde,它的循环节就是它本身,等于说并没有循环。而常见的是类似于abcbac这种(len = 6, l = 3)。有时候还会求周期个数(循环节个数):num = len/i;
2️⃣len%l != 0,就是字符串不是循环节的整数倍,没有循环到底,例如abcabcab(注意这里的nextt[8]=5(abcab),所以l = 8-5=3),
8%3==2 != 0,就是说最后一个循环节没有循环到底,只有2个(ab),要补上l-len%l=1个。
故涉及到循环节的问题,只要考虑三组类型:abcabc,abcabcab,abcdef就可以避免考虑不全的情况了。
③前后缀问题(nextt数组的应用二):
1️⃣nextt数组的定义见②,就是前后缀的最大相等长度,通过一个while循环,不断迭代,直到nextt[i]为0,可以求出字符串所有的前后缀相等的长度。例如,ababcababababcabab,最长的相等长度为nextt[18]=9(ababcabab),然后nextt[9]=4(abab),nextt[4]=2(ab), nextt[2]=0。注意,括号的字符串既可以理解为前缀,也可以理解为原字符串的前后缀的组合(由于之前前后缀的匹配带来的关系)。
2️⃣扩展kmp:扩展kmp中用到了两个数组:nextt和ext,其中nextt[i]数组的定义是:p[i.....(m-1)]与p[0....(m-1)]的最长公共前缀,也就是p串从i开始后面的字符串p1与整个p串的最长公共前缀。注意与kmp算法中的nextt数组的区别:kmp算法中的nextt[i]表示的是字符串p[0...(i-1)]这个字符串的最大相等前后缀的长度。举个栗子:abaabb。在kmp算法中,nextt的值除了nextt[0]=-1外,其余都为0。而在扩展kmp中,nextt[3]=2,因为nextt[3]表示的是字符串p1[3...5](即abb)与p(即abaabb)的最大公共前缀的长度,也就是2。
它的nextt[i]=m可以理解为p字符串前面m个字符在后面的第i个位置又出现了。 不难理解:nextt[0]总是等于m。
ext[i]数组:定义是s[i....(n-1)]与p[0....(m-1)]的最大公共前缀。也就是主串s的从i开始的后面的字符串s1与模式串p的最长公共前缀。当ext[i]=m时,也就是s1==p,说明p串在s串的第i个位置出现了,也就是kmp中的匹配成功,所以说扩展kmp是kmp的一种扩展。
ps:扩展kmp其实求得的是两个字符串的最大前缀,不过可以转化为两个字符串的最大相等前后缀长度(没错,就是上面kmp算法的nextt的应用)。具体就是加一个判断当if(ext[i]==n-i) 此时s[i....(n-1)]字符串就是s串的后缀,并且和p串的长度为ext[i]的前缀相等。
3️⃣环形串(可以从不同的下标开始形成n个串)性质:
①就是环形串的n个串的个数都一样,特别的,当原串是类似于abcabc这种“满循环串”时,每个串的个数就等于(len/循环节),也就是周期个数,而串的种类就等于一个循环节的长度。
②涉及到环串,还有一个经常用到的处理方式,就是倍增一次,将s串变成s+s,这样就不用取余什么的操作了。(这题没用到)
A - Number Sequence
题意:
给你字符串s和p,问你p在s串中首次出现的下标,若没有出现,则返回-1。
思路:裸单个字符串匹配问题(s1在s2中匹配,①1️⃣类型),一开始直接用kmp写得,刚刚试了一下,TLE了,这题数据量1e6,T也是意料之中,所以数据量很大时,还是老老实实敲kmp板子吧。
AC代码(kmp板子):
#include
TLE代码(用的strstr函数):
#include
B - Oulipo
题意:
给你两个字符串s和p,问你s中有多少个p(可重叠)?
思路:裸的kmp板子(①2️⃣类型)。
代码:
#include
C - 剪花布条
题意:
给你两个字符串s和p,问你s中有多少个p(不可重叠)?
思路:裸的kmp板子(①2️⃣类型)。
代码:
#include
X - Wow! Such Doge!
题意:
水题一枚,给你一段文字,问你里面有多少doge(不区分大小写)
思路:
直接用kmp匹配就行。
由于不区分大小写,所以在kmp匹配函数中,比较时都比较大写(或小写)。
另外由于是读入一篇文字,所以不能用%s读入,可以直接用%c读,一直读到文件结束就行。
代码:
#include
D - Cyclic Nacklace
题意:
给你一串字符串,问你至少需要添加多少字符才能使它至少循环两次。
思路:
裸的循环节问题(②2️⃣类型),直接套公式ans = l-len%l。需要注意的是,abcde这种,直接套公式得到是ans = 0,不过题目要求字符串至少循环两次,所以ans应该为5,只要特判一下len ?= l 就可以了。
代码:
#include
E - Period
题意:
给你一个字符串,求它各个"满循环”(len%l == 0)前缀字符串 ,输出满足条件的前缀的首个下标(在原字符串中的)以及周期个数(循环节个数)
思路:
先对原字符串进行一次pre_kmp(),得到nextt数组,然后遍历原字符串的所有前缀,然后找出满足条件的前缀(len%l == 0),输出相应的下标以及个数(len%l)。
有一个wa点,就是abcde这种满足len%l == 0的伪循环。
代码:
#include
F - Power Strings
题意:
给你一个字符串,问你可以用多少的循环节拼接而成。
思路:
其实就是求循环节个数的问题,公式为num = len/l。然后考虑一下abcabc abcabcab abcdef这三种类型就可以了。可以发现对于abcabcab这种类型,尽管循环节为abc,并且存在两个abc,不过按照题意却要输出1。
代码:
#include
G - Seek the Name, Seek the Fame
题意:
给你一个字符串,问你的它各个前后缀相等的长度。
思路:
根据nextt的定义以及理解,可以通过循环迭代,求出各个前后缀相等的长度(③1️⃣)。注意一点的是,这里的前后缀定义,前缀和后缀可以是原串全部,所以原串的长度一定是其中的一个答案。
代码:
#include
H - Blue Jeans
题意:给你m个长度为60的字符串,问你在这m个字符串中都出现的最长字符串有多长?
思路:考虑这题的m不会大于10,而且每个字符串也只有60的长度,所以可以采用暴力大法,枚举第一个串的所有子串,然后依次在剩下的m-1个串中查找。这里枚举一个串的所有子串可以采用两个for循环,外层是子串的长度,内层是子串开始的下标。截取函数可以采用strncpy(具体用法可以看:https://blog.csdn.net/vaeloverforever/article/details/82048632)。最后需要注意,最大子串如果长度小于3,需要输出“no significant commonalities”。
ps:这题数据量很小,所以匹配查找子串时,除了可以用kmp,也可以直接用strstr函数
代码(kmp匹配查找):
#include
代码(strstr函数匹配查找):
#include
I - Simpsons’ Hidden Talents
题意:题目前面巴拉巴拉说了一大通,其实也就最后一句话有用:
Write a program that, when given strings s1 and s2, finds the longest prefix of s1 that is a suffix of s2.
就是给你两个串s1和s1,要求一个最大长度的串s,并且s满足既是s1的前缀,也是s2的后缀。
思路:
当初写的时候看了别人的题解,按照他的思路写的:题目要求的是两个串的最大相等前后缀,可以联想到kmp算法的nextt的运用(③1️⃣),不过kmp算法适用于单个字符串,所以可以将两个字符串连接起来,合成s1+s2,当时看到还是挺激动的,这个办法好呀,注意就是只要求一下nextt数组就行了啊,他题解还提醒了一个wa点,就是求出的答案不能超过原串s1和s2的长度,这是肯定的,前后缀的长度怎么可能会比原串长呢,只要在ans,len1,len2中取最小的就是答案了。于是我很快写好了,交上去也就a了,也就没多想,直接写下一题了。
刚刚来到这题,我发现可以用扩展kmp(③2️⃣)写嘛,只要加一个判断就可以把最长公共前缀转化为最大长度的前后缀。于是又写了一份代码,交了一发,wa了。。。自己不服气啊,试了一些自己编的数据都是对的呀,于是翻出自己第一次a的代码,开始用上篇博客介绍的对拍程序开始对拍,拍啊拍,果然发现一个不同的样例:s1=y s2=asfaya,我之前"ac"代码输出"a 1",我的"wa"代码输出"0",我一看傻眼了。。。。为毛我的"wa"代码输出了正确答案,我的"ac"代码却输出错误答案???
仔细研究自己的"ac”代码,发现的确有问题,当然思路是没问题的,就是最后对答案的处理有问题,不应该简单的在ans,len1,len2中取最小值,应该不断迭代nextt数组(见③ 1️⃣),直到比len1和len2都小。
改完之后,再和自己的"wa"对拍,发现对拍了1000份样例,都是一样的。。。可能是随机数生成的不够好吧,没有特殊数据。没办法,只能搜了一篇别人用扩展kmp写的代码,先copy别人的main函数,发现还是wa,再copy扩展kmp函数就a了,说明就是扩展kmp写错了。。。哎 还是扩展kmp写的少啊,照着板子抄都抄错了。。。。抄错了两个地方:
①在EKMP函数中把唯一一处的nextt写错成ext了 ②while条件括号中的j写错成i+j。
不过我这次对拍也算史无前例了。。。没找出wa代码的问题,反而找出ac代码的问题。。。看来杭电oj这题的数据是真的弱啊。
一开始错误“ac"代码(kmp+字符串拼接):
#include
对上面代码改后的ac代码(kmp代码):
#include
AC代码(扩展kmp):
#include
J - Count the string
题意:给你一个字符串s,求它的各个前缀个数和。
思路:额。。我是看了别人的题解的。。是kmp+dp,
dp[]数组:以 i 结尾的串中所有前缀的计数和
状态转移方程: dp[i] = dp[next[i]] + 1;
果然dp是我一个很大的短板啊。。。很难想到。。。。
另外一种解法是:https://www.cnblogs.com/acjiumeng/p/6819026.html
http://972169909-qq-com.iteye.com/blog/1114968(这个讲的很清楚)
代码(dp):
#include
K - Clairewd’s message
题意:
题意比较难理解,就是说给定两组字符串,第一组只有26个字符表对应明文中a,b,c,d....z,可以对明文进行加密。
第二组字符串是给定的密文+明文,明文可能不完整(缺失或没有),叫你补完且整个密文+明文是最短的
如果有多种明文则取最大的明文
思路:由于明文和密文存在对应关系,可以直接这个关系进行匹配,找出匹配的部分,也就找出了密文和明文的分界点,然后再对应加密表补上缺的明文就行。直接从中间开始,以它作为分界点进行,如果失配就把分界点前移一位,一直找到一份分界点,使得完全匹配,然后再补上缺的。搜了一些题解,貌似还可以用ekmp进行匹配。我是直接暴力的,也过了,可能数据比较水。
代码:
#include
L - Substrings
题意:给你n个字符串,问你它们公共子串的最大长度是多少,这里的子串可以是原串的顺序,也可以是原串的逆序,也就是反串。
思路:
同H题一样,直接暴力枚举其中一个串的所有子串,然后在其他串中进行匹配。这里所要枚举的串,我选择了最短的串,这样可以减少枚举量,在读入的时候就找出最短的串并记录下来。匹配子串时,可以直接用strstr函数,因为每个字符串长度很短,而且数目也很小,所以不会超时,如果数据很大的话,就得换成kmp匹配了。
另外,截取子串时,枚举起点和长度,这样同时也可以直接调用strncpy函数进行截取,反转的时候,直接用reverse函数,这个反转函数即适用于字符串,也适用于字符数组。
需要注意的是,char *p; strncpy(p,s+i,l);这样写是不对的,因为p只是一个字符指针,没有存储空间,需要动态申请,或者直接char p[maxn](需要memset)。
代码:
#include
M - Corporate Identity
题意:这题就是L题的一个简化版嘛,就是去掉了反串,直接问最大长度的公共子串。
思路:还是同L题一样的思路,这次我用的字符串类型,不是字符数组,相应的截取函数就用的是substr
这里用strstr还是kmp匹配都能过,我代码里两种方法都写了。
代码(strstr函数和kmp匹配都有相应的代码):
#include
N - String Problem
题意:给你一个字符串s(长度为n),按下标开始编号为1~n,形成n个串,每个串的起点是s[编号-1],当然,这个串是个环形串,问你字典序最大和字典序最小的串的编号分别是多少,以及这个串在原串出现的个数?
思路:这个问题关键在于如何找到字典序最大和最小的串,一开始,用set容器或者排序,捣鼓了半天,一直超时,最后发现这个过程需要一个O(n)的算法,于是找到了最大和最小表示法这种方法,这个方法可以在遍历一遍原串后,找出字典序最大或者最小的串。关于这个算法可以看:https://blog.csdn.net/cillyb/article/details/78058174
很常见的一个算法,也很容易写,容易写错的地方就是①不匹配的时候,k要归零。②i(j)在增加的时候,如果等于j(i),要跳过,因为i==j时,是同一个串,没有比较的必要。
另外题目还要求个数,但是由于是环形串,所以有个性质,1️⃣就是这n个串的个数都一样,特别的,当原串是类似于abcabc这种“满循环串”时,每个串的个数就等于(len/循环节),也就是周期个数,而串的种类就等于一个循环节的长度。
2️⃣涉及到环串,还有一个经常用到的处理方式,就是倍增一次,将s串变成s+s,这样就不用取余什么的操作了。(这题没用到)
代码:
#include
O - How many
题意:
给你一些环串,问你一共有多少不同的环串。
思路:
由于是环串,所以没法直接比较是否相同,因为环串有多种表示方式,因此需要统一格式,可以用最大(最小)表示法,把各个环串统一成一样的格式。再进行比较就行了。
计算不同环串的个数,可以用set容器。
不过还有个问题就是,你之前虽然得到了各个环串的最大(小)表示法的起始下标,可是如何得到你所表示的这个串呢,这里就用到上一题提到的环串的基本操作啦:倍增~就是让s =s+s,再用一个小技巧就行,比如这个串最大表示的起始下标为startt,那么你可以另s[istartt+len]='\0',这里的s是已经倍增过的,len是没有倍增过的s的长度,这样就截取了一个长度为len的串了。
代码:
#include
P - Period II
题意:
给你一个字符串 s 求出所有满足s[i] == s[i+p] ( 0 < i+p < len )的 p
思路:
其实就是这个字符串的后缀与前缀的最大匹配 next[N],然后用最大匹配的串继续找匹配的前缀,比如下面的数据:
aaabaaa:--> P = 4 <---> next[7] = 3
aaabaaa:--> P = 5 <---> next[3] = 2
aaabaaa:--> P = 6 <---> next[2] = 1
aaabaaa:--> P = 7 <---> next[1] = 0
可以发现,就是迭代nextt数组,输出len-nextt[]
代码:
#include
Y - Theme Section
题意:
给你一个字符串s,问你它是否满足“EAEBE”这种形式,其中E表示一段字符,就是说E这段字符在s的开头、中间、结尾都出现了。让你输出E。
思路:
由于E在首尾都出现了,所以可以考虑先找出最大前后缀,然后再在中间匹配这个最大前后缀。
找最大前后缀,直接用kmp中求nextt数组就行。在中间匹配可以直接用strstr这个函数。
代码:
#include
