Google OR-Tools(七) 网络流 Network Flows
本文参考Google OR-Tools官网文档介绍OR-Tools的使用方法。
1 网络流模型
网络流问题(Network Flows)是图论领域的一个经典问题,由多个节点和节点间的连接构成一个网络,在这个网络上需要考虑最大效率地传输。和其他图问题相比,网络流最关键的一个约束就是网络上的每条边都有固定的容量,在这条边上传输的最大量不能超过容量,拿现实中的例子来举例,比如一条网路上的数据上传有最大流量限制,一条交通要道上通过的车流量有上限。
数学上,将一个网络流定义为一个图 G = ( V , E ) G=(V,E) G=(V,E), V V V表示图上所有的节点集合, E E E表示图上所有的边集合,对于图 G G G,有:
- 每条边具有方向性,表示这上面的流的可流动方向
- 每条边 e ∈ E e \in E e∈E,都有一个非负数的容量 c e c_e ce,例如下面示意图中A和B间的容量为4
- 有一个源节点 s ∈ V s \in V s∈V,源节点只有流出,没有流入
- 有一个终结点 t ∈ V t \in V t∈V,终结点只有流入,没有流出

在图 G G G上,定义函数 f ( e ) f(e) f(e)表示边 e e e上的流的大小,对于 f ( e ) f(e) f(e)有着基本约束 0 ≤ f ( e ) ≤ c ( e ) 0\leq f(e)\leq c(e) 0≤f(e)≤c(e)
2 最大流问题 Maximum Flows
2.1 线性规划建模
在基本的流模型上,加上一个流平衡约束,对于一个除了 s s s和 t t t的节点 v v v,有
∑ e i n t o v f ( e ) = ∑ e l e a v i n g v f ( e ) \begin{aligned} \sum_{e\ into\ v} f(e)=\sum_{e\ leaving\ v} f(e)\\ \end{aligned} e into v∑f(e)=e leaving v∑f(e)
这个约束表示对于节点 v v v,流入的量等于流出的量
然后我们定义函数 v ( f ) v(f) v(f)表示网络流上流的总量值:
v ( f ) = ∑ e o u t o f s f ( e ) \begin{aligned} v(f)=\sum_{e\ out\ of\ s}f(e)\\ \end{aligned} v(f)=e out of s∑f(e)
即从 s s s节点流出的总量。有了这些信息,我们就可以把最大流问题定义为,对于一个网络流 G G G,找到它的最大的 v ( f ) v(f) v(f),也就是可以从节点 s s s流出的最大流量
最大流问题显然是一个线性规划问题。我们以上面的网络流示例图为例,要求的变量就是每条边上的流量大小 f ( e ) f(e) f(e),如下图中的 f S A f_{SA} fSA, f S C f_{SC} fSC, . . . ... ...

需要满足容量约束
f S A ≤ 4 f S C ≤ 3 f A B ≤ 4 . . . \begin{aligned} f_{SA}\leq 4 \\ f_{SC}\leq 3 \\ f_{AB}\leq 4 \\ ... \end{aligned} fSA≤4fSC≤3fAB≤4...
也要满足平衡约束,即流入与流出量相等
f S A = f A B f S C + f B C = f C D f A B = f B C + f B T . . . \begin{aligned} f_{SA}=f_{AB} \\ f_{SC}+f_{BC}=f_{CD} \\ f_{AB}=f_{BC}+f_{BT} \\ ... \end{aligned} fSA=fABfSC+fBC=fCDfAB=fBC+fBT...
而问题的目标则是
m a x i m i z e f S A + f S C \begin{aligned} maximize\ f_{SA}+f_{SC} \end{aligned} maximize fSA+fSC
既然是线性规划问题(如果要求流量为整数则是整数线性规划),那么我们就可以使用通用的线性规划求解器来解算了。不过对于最大流问题,人们一般会使用一些专用的算法,例如经典的Ford-Fulkerson算法
2.2 Ford-Fulkerson算法
Ford-Fulkerson算法在1956由 L. R. Ford Jr. 和 D. R. Fulkerson提出,这是一种贪心式算法,其基本思想是一旦某条从 s s s到 t t t的路径存在可承载流量,我们给总流量加上这个值,这里的路径称之为扩充路径(augmenting path),重复这个过程直到没有任何扩充路径剩下。
还是拿上面那个图来举例,首先我们选择路径S->A->B->T,这条路径上的最小容量是BT边上的2,因此将总流量从零变到2;接着选择S->C->D->T,最小容量是3,总流量变成5;这时还剩下最后一条路径S->A->B->C->D->T(因为边BT和SC上已经没有剩余容量了,这两条边无法再通过),注意这条路径的最小容量不是3,而是2,因为边SA和AB上已经只有2单位的剩余容量了,这时总流量是7,这也是最终结果。

Ford-Fulkerson算法的伪代码如下:
flow = 0
for each edge (u, v) in G:
flow(u, v) = 0 //初始化所有边的流量为零
while there is a path, p, from s -> t in residual network G_f: //不断地寻找扩充路径
residual_capacity(p) = min(residual_capacity(u, v) : for (u, v) in p) //路径的剩余容量是该路径上边的最小剩余容量
flow = flow + residual_capacity(p)
for each edge (u, v) in p: //需要更新这条路径上边的剩余流量情况
if (u, v) is a forward edge:
flow(u, v) = flow(u, v) + residual_capacity(p) //如果是前向边,则加大流量
else:
flow(u, v) = flow(u, v) - residual_capacity(p)
return flow
伪代码中涉及几个新的术语:剩余网络(residual graph)、前向边(Forward edges)和后向边(Backward edges)。在算法的每次迭代中,都需要首先构建由前向边和后向边构成的剩余网络 G f G_f Gf:
- G f G_f Gf中的节点和原网络一致
- 构建前向边,即对原网络 G G G中的每一条存在 f ( e ) ≤ c e f(e)\leq c_e f(e)≤ce情况的边 e ( u , v ) e(u,v) e(u,v),在剩余网络 G f G_f Gf中构建容量为 c e − f ( e ) c_e-f(e) ce−f(e)的边 e ′ ( u , v ) e^{'}(u,v) e′(u,v)
- 构建后向边,即对原网络 G G G中的每一条存在 f ( e ) > 0 f(e)> 0 f(e)>0情况的边 e ( u , v ) e(u,v) e(u,v),在剩余网络 G f G_f Gf中构建容量为 f ( e ) f(e) f(e)的边 e ′ ( v , u ) e^{'}(v,u) e′(v,u)(注意这是反向的)
回到上面的例子,在处理完路径S->A->B->T后,可以构建如下图所示的剩余网络,黑线表示前向,红线表示后向

伪代码中另一个需要指出的点是,Ford-Fulkerson算法并没有指定如何在剩余网络中找到扩充路径,这一步可以由不同的子算法实现,例如深度优先遍历。正因为这个原因,Ford-Fulkerson算法有时候会被强调为“方法”而不是“算法”,它只提供了大体的算法步骤。
虽然Ford-Fulkerson算法采用了贪心式的思想,但是它得到的解可以根据最大流-最小切理论(Max-flow Min-cut)证明就是最优的,因此解决最大流问题通常都会使用Ford-Fulkerson算法及其衍生算法。从复杂度上来说,如果变量都是整数,Ford-Fulkerson算法的复杂度为 O ( E f ∗ ) O(Ef^{*}) O(Ef∗),这里 E E E表示网络中的边数, f ∗ f^{*} f∗网络的最大流。
2.3 OR-Tools求解
OR-Tools提供了专门计算最大流问题的MinCostFlow对象,我们使用它写个简单的demo
我们就计算上面举得网络流例子,将图中6个节点从0到5编号,并用数组存储边信息,比如第0条边是从0到1,相应的数据存储为从start_nodes[0]=0到end_nodes[0]=1的容量是capacities[0]=4

// Define three parallel arrays: start_nodes, end_nodes, and the capacities
// between each pair. For instance, the arc from node 0 to node 1 has a
// capacity of 4.
int numNodes = 6;
int numArcs = 7;
int[] start_nodes = { 0, 1, 2, 0, 2, 5, 4};
int[] end_nodes = { 1, 2, 3, 5, 5, 4, 3};
int[] capacities = { 4, 4, 2, 3, 3, 6, 6};
创建 SimpleMaxFlow对象,并调用AddArcWithCapacity方法告知求解器每条边的容量信息
// Instantiate a SimpleMaxFlow solver.
MaxFlow maxFlow = new MaxFlow();
// Add each arc.
for (int i = 0; i < numArcs; ++i)
{
int arc = maxFlow.AddArcWithCapacity(start_nodes[i], end_nodes[i],
capacities[i]);
if (arc != i) throw new Exception("Internal error");
}
int source = 0;
int sink = 3;
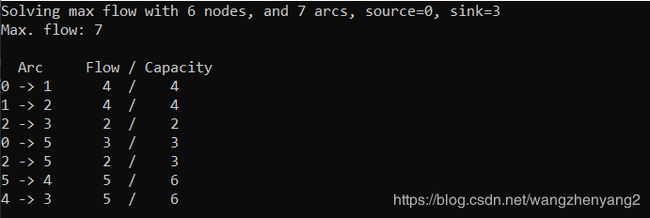
然后就可以求解并获取最大流的值和每条边的流量
// Find the maximum flow
var solveStatus = maxFlow.Solve(source, sink);
if (solveStatus == MaxFlow.Status.OPTIMAL)
{
Console.WriteLine("Max. flow: " + maxFlow.OptimalFlow());
Console.WriteLine("");
Console.WriteLine(" Arc Flow / Capacity");
for (int i = 0; i < numArcs; ++i)
{
Console.WriteLine(maxFlow.Tail(i) + " -> " +
maxFlow.Head(i) + " " +
string.Format("{0,3}", maxFlow.Flow(i)) + " / " +
string.Format("{0,3}", maxFlow.Capacity(i)));
}
}
else
{
Console.WriteLine("Solving the max flow problem failed. Solver status: " +
solveStatus);
}
using System;
using Google.OrTools.Graph;
namespace MaximumFlowProblem
{
class Program
{
static void Main(string[] args)
{
// Define three parallel arrays: start_nodes, end_nodes, and the capacities
// between each pair. For instance, the arc from node 0 to node 1 has a
// capacity of 4.
int numNodes = 6;
int numArcs = 7;
int[] start_nodes = { 0, 1, 2, 0, 2, 5, 4};
int[] end_nodes = { 1, 2, 3, 5, 5, 4, 3};
int[] capacities = { 4, 4, 2, 3, 3, 6, 6};
// Instantiate a SimpleMaxFlow solver.
MaxFlow maxFlow = new MaxFlow();
// Add each arc.
for (int i = 0; i < numArcs; ++i)
{
int arc = maxFlow.AddArcWithCapacity(start_nodes[i], end_nodes[i],
capacities[i]);
if (arc != i) throw new Exception("Internal error");
}
int source = 0;
int sink = 3;
Console.WriteLine("Solving max flow with " + numNodes + " nodes, and " +
numArcs + " arcs, source=" + source + ", sink=" + sink);
// Find the maximum flow
var solveStatus = maxFlow.Solve(source, sink);
if (solveStatus == MaxFlow.Status.OPTIMAL)
{
Console.WriteLine("Max. flow: " + maxFlow.OptimalFlow());
Console.WriteLine("");
Console.WriteLine(" Arc Flow / Capacity");
for (int i = 0; i < numArcs; ++i)
{
Console.WriteLine(maxFlow.Tail(i) + " -> " +
maxFlow.Head(i) + " " +
string.Format("{0,3}", maxFlow.Flow(i)) + " / " +
string.Format("{0,3}", maxFlow.Capacity(i)));
}
}
else
{
Console.WriteLine("Solving the max flow problem failed. Solver status: " +
solveStatus);
}
}
}
}
3 最小花费流问题 Minimum Cost Flows
3.1 数学模型
最小花费流问题是在最大流问题基础上添加供应/消耗约束和每条边的花费扩展而来的,问题的目标变为找到使得总花费最小的流。
在最小花费流问题上,没有了源节点(source)和终结点(sink),取而代之的是供应(supply)和消耗(demand)结点,每个供应点都对应一个正数,表示增加到流上的材料数量,可以拿现实中的仓库来映射,仓库可以供应一定数量的产品或材料;而每个消耗点则对应一个负数,表示它需要消耗多少单位的材料;如果一个结点既不是供应结点也不是消耗结点,则它就是一个中转点。供应/消耗信息带来一个必要约束:
- 对每个结点,流出量减去流入量要等于这个结点的供应(或消耗)值
同时,每条边上除了容量信息,还对应一个花费值,表示通过每单位的流量需要花费多少,例如从0到1的边的单位花费为2,如果通过了4单位的流,则在这条边上需要花费8。由此我们的目标就是在满足所有消耗点的情况下使得总的花费最小。事实上在这个目标下,最小花费流问题中就必须存在消耗结点,因为如果没有消耗点,那么总流量为零就是最优解。
下面这副图示意了一个典型的最小花费流问题,每条边对应两个数字,第一个表示容量,第二个表示花费;每个结点对应一个数字,表示供应或消耗量

最小花费流更为严格的数学描述为:
G = ( V , E ) G=(V,E) G=(V,E)是由结点集合 V V V和边集合 E E E构成的有向图网络,对于每条边 e ( u , v ) ∈ E e(u,v)\in E e(u,v)∈E,对应一个 c e c_e ce表示这条边的容量限制,同时还对应一个 a e a_e ae表示单位流的花费值;对于每个结点 u ∈ V u\in V u∈V都对应一个 b u b_u bu,这个值表示供应或消耗值, b u > 0 b_u>0 bu>0表示供应,反之为消耗,如果为零则该结点为中转点;定义函数 f ( e ) f(e) f(e)表示边 e ( u , v ) e(u,v) e(u,v)上的流量大小,那么问题的目标就可表示为:
M i n i m i z e ∑ e ( u , v ) ∈ E a e f ( e ) \begin{aligned} Minimize\ \sum_{e(u,v)\in E}a_ef(e) \end{aligned} Minimize e(u,v)∈E∑aef(e)
而两个约束则为:
∑ e ( u , v ) ∈ E f ( e ) − ∑ e ′ ( v , u ) ∈ E f ( e ′ ) = b u , u ∈ V 0 ≤ x e ≤ c e , e ( u , v ) ∈ E \begin{aligned} &\sum_{e(u,v)\in E}f(e) - \sum_{e^{'}(v,u)\in E}f(e^{'})=b_u\ ,\ u\in V \\ &0\leq x_e\leq c_e\ ,\ e(u,v)\in E\\ \end{aligned} e(u,v)∈E∑f(e)−e′(v,u)∈E∑f(e′)=bu , u∈V0≤xe≤ce , e(u,v)∈E
第一个约束就是指的流出量减流入量要等于供应/消耗值,第二个约束是容量约束
对于最小花费流问题,一般也采用一些专用算法,其中最常见的是网络单纯形算法(Network simplex algorithm),我没有研究过,这里就不介绍了。
3.2 OR-Tools求解
OR-Tools也提供了专门用于计算最小花费流问题的MinCostFlow对象。我们以上面的图为例写个demo,首先定义数据
// Define four parallel arrays: sources, destinations, capacities, and unit costs
// between each pair. For instance, the arc from node 0 to node 1 has a
// capacity of 15.
int numNodes = 5;
int numArcs = 9;
int[] startNodes = { 0, 0, 1, 1, 1, 2, 2, 3, 4 };
int[] endNodes = { 1, 2, 2, 3, 4, 3, 4, 4, 2 };
int[] capacities = { 15, 8, 20, 4, 10, 15, 4, 20, 5 };
int[] unitCosts = { 4, 4, 2, 2, 6, 1, 3, 2, 3 };
// Define an array of supplies at each node.
int[] supplies = { 20, 0, 0, -5, -15 };
然后定义MinCostFlow对象,再调用AddArcWithCapacityAndUnitCost方法告知MinCostFlow对象每条边的容量和费用;调用SetNodeSupply方法告知每个结点的供应/消耗量
// Instantiate a SimpleMinCostFlow solver.
MinCostFlow minCostFlow = new MinCostFlow();
// Add each arc.
for (int i = 0; i < numArcs; ++i)
{
int arc = minCostFlow.AddArcWithCapacityAndUnitCost(startNodes[i], endNodes[i],
capacities[i], unitCosts[i]);
if (arc != i) throw new Exception("Internal error");
}
// Add node supplies.
for (int i = 0; i < numNodes; ++i)
{
minCostFlow.SetNodeSupply(i, supplies[i]);
}
最后计算并显示结果:
// Find the min cost flow.
var solveStatus = minCostFlow.Solve();
if (solveStatus == MinCostFlow.Status.OPTIMAL)
{
long optimalCost = minCostFlow.OptimalCost();
Console.WriteLine("Minimum cost: " + optimalCost);
Console.WriteLine("");
Console.WriteLine(" Edge Flow / Capacity Cost");
for (int i = 0; i < numArcs; ++i)
{
long cost = minCostFlow.Flow(i) * minCostFlow.UnitCost(i);
Console.WriteLine(minCostFlow.Tail(i) + " -> " +
minCostFlow.Head(i) + " " +
string.Format("{0,3}", minCostFlow.Flow(i)) + " / " +
string.Format("{0,3}", minCostFlow.Capacity(i)) + " " +
string.Format("{0,3}", cost));
}
}
else
{
Console.WriteLine("Solving the min cost flow problem failed. Solver status: " +
solveStatus);
}
using System;
using Google.OrTools.Graph;
namespace MinCostFlowProblem
{
class Program
{
static void Main(string[] args)
{
// Define four parallel arrays: sources, destinations, capacities, and unit costs
// between each pair. For instance, the arc from node 0 to node 1 has a
// capacity of 15.
int numNodes = 5;
int numArcs = 9;
int[] startNodes = { 0, 0, 1, 1, 1, 2, 2, 3, 4 };
int[] endNodes = { 1, 2, 2, 3, 4, 3, 4, 4, 2 };
int[] capacities = { 15, 8, 20, 4, 10, 15, 4, 20, 5 };
int[] unitCosts = { 4, 4, 2, 2, 6, 1, 3, 2, 3 };
// Define an array of supplies at each node.
int[] supplies = { 20, 0, 0, -5, -15 };
// Instantiate a SimpleMinCostFlow solver.
MinCostFlow minCostFlow = new MinCostFlow();
// Add each arc.
for (int i = 0; i < numArcs; ++i)
{
int arc = minCostFlow.AddArcWithCapacityAndUnitCost(startNodes[i], endNodes[i],
capacities[i], unitCosts[i]);
if (arc != i) throw new Exception("Internal error");
}
// Add node supplies.
for (int i = 0; i < numNodes; ++i)
{
minCostFlow.SetNodeSupply(i, supplies[i]);
}
// Find the min cost flow.
var solveStatus = minCostFlow.Solve();
if (solveStatus == MinCostFlow.Status.OPTIMAL)
{
long optimalCost = minCostFlow.OptimalCost();
Console.WriteLine("Minimum cost: " + optimalCost);
Console.WriteLine("");
Console.WriteLine(" Edge Flow / Capacity Cost");
for (int i = 0; i < numArcs; ++i)
{
long cost = minCostFlow.Flow(i) * minCostFlow.UnitCost(i);
Console.WriteLine(minCostFlow.Tail(i) + " -> " +
minCostFlow.Head(i) + " " +
string.Format("{0,3}", minCostFlow.Flow(i)) + " / " +
string.Format("{0,3}", minCostFlow.Capacity(i)) + " " +
string.Format("{0,3}", cost));
}
}
else
{
Console.WriteLine("Solving the min cost flow problem failed. Solver status: " +
solveStatus);
}
}
}
}