Python游戏之运动物体寻路——A星算法与扩展
上一篇文章主要完成了游戏地图的创建,其中简单为游戏寻路做了一点准备,就是格栅背景地图。游戏场景中的各种山川、河流、楼阁等都都可以视为为某种运动精灵的障碍物,那么精灵如何绕过障碍物运动都自己的目的地呢?目前关于寻路的算法有很多,最常见的就是A-Star算法,也叫A星算法。
典型的A-star算法处理的是运动物体和格栅大小一致,如果运动物体比格栅小,自然没有任何问题。如果运动物体比格栅大,典型的A-star算法就不能处理了。那么是不是A-star方法就不能处理了呢?不是,针对这个问题,国外有人提出了叫做 Brushfire的算法。据说得google才能找到。我简单看了一下,应该也是可以实现的。有兴趣的朋友可以自行探索。
典型的Astar算法网上有很多详细的讲解,有一位大拿的文章请参考,还有一些前人给出了C/C++/JAVA/JSP等各种语言的实现。这里就不再重复了。
本文解决的问题是大于格栅大小的物体的寻路问题,并尽可能实现任何大小的物体寻路。下面有几个示意图可以先看一下。
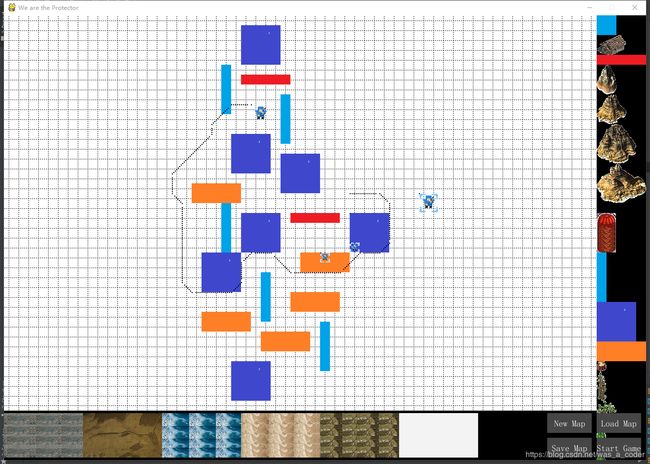
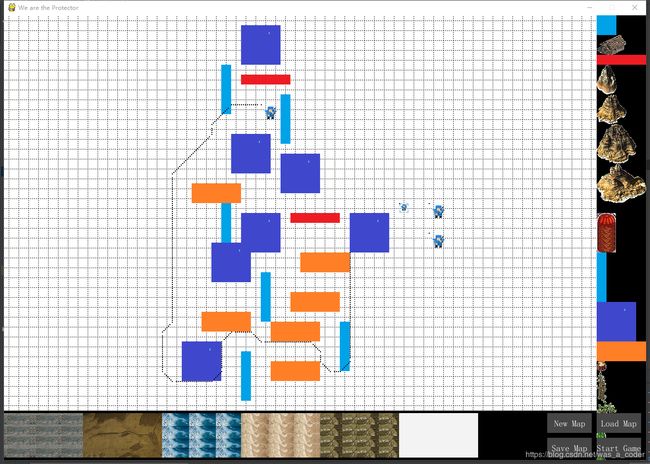

为了方便理解,这里用虚线展示精灵的运动路径,实际上是精灵的左上角运动轨迹。有些Astar算法只允许精灵在水平和垂直方向运动,有些可以8个方向(45度角)。这其实没有本质的区别,只是在寻路过程中对合格邻接点的筛选策略不同而已。完全可以根据自己的需要来处理。
好了,现在开始展示A-star算法。
既然涉及到格栅,那么格栅怎么描述呢?就是点的集合。先描述点:
class Node:
def __init__(self, point, target, father=None):
self.point = point
self.father = father
if father is not None:
self.gCost = father.gCost + self.get_gCost(father.point)
self.hCost = self.get_hCost(target)
self.fCost = self.gCost + self.hCost
else:
self.gCost = 0
self.hCost = 0
self.fCost = 0
# 计算自己到父节点的gCost。如果到父节点为 45 度方向,设置 gCost 为 14,否则设为 10
def get_gCost(self, father):
if abs(self.point[0] - father[0]) + abs(self.point[1] - father[1]) == 2:
return 14
return 10
def get_hCost(self, target):
return (abs(target[0] - self.point[0]) + abs(target[1] - self.point[1])) * 10
def reset_father(self, father, newgCost):
if father is not None:
self.gCost = newgCost
self.fCost = self.gCost + self.hCost
self.father = father
关于cost的设置方法,有很多策略,有兴趣的可以进一步研究。这里使用最简单的实现,便于理解。
point是什么呢?就是格栅点的(X轴索引,Y轴索引),一个Tuple。
有了Node,下面就是A-Star了。
类属性定义:
class AStar:
# stat and target 是Tuple (x, y), 是格栅的索引点,不是像素坐标。
# size 为寻径主体的大小,表示边长为格栅尺寸的倍数
# 对于非正方形主体,将其边长大的边计算size就可以
def __init__(self, grids, start, target, size):
self.grids = grids
self.size = size
self.start = self.adjust_position(start)
self.target = self.adjust_position(target)
self.startNode = Node(self.start, self.target, None)
self.targetNode = Node(self.target, self.target, None)
# 开放列表和封闭列表使用集合,避免重复.
# openSet 和 closeSet 字典结构,key 为 point, value 为 node
self.openSet = dict()
self.closeSet = dict()
# 存储从起点到终点的路径, 逆序则为回程路径。注意,路径包含起点和终点。
# 路径简化后包含起点、拐弯点和目的点。
self.path = []
def init_set(self):
self.openSet.clear()
self.closeSet.clear()
大家看到self.start 和 self.target,为什么没有直接使用精灵给出的起点和终点呢?因为很多时候玩家给精灵的目的点有时候可能是不可达的,也就是障碍物,玩家可能要求精灵去给定目的地附近的一个区域。起点位置呢?如果精灵是自动生产的,初始的位置有可能在障碍物里面,那么精灵自己是无法走出障碍物的,就需要调整精灵的起点位置。
那么如何调整呢?有两种策略,最简单的策略就是将精灵的起点和目的地调整为给定位置附近最近的一个可达点(合格的邻接点),另一种策略就是爱咋地咋地,精灵找不到路就呆在原地好了。看你的需要了,还有一种可能,调整范围不够大时,如论如何调整都不可达,被障碍物包围分离了,那就不在本文讨论范围了,重新设计你的地图吧。
def find_min_fCost_node(self):
# 在 当前路径中寻找代价最低节点作为寻找下一个节点的父节点。
_min = 99999
_point = self.start
for point, node in self.openSet.items():
if _min > node.fCost:
_min = node.fCost
_point = point
return self.openSet[_point]
def add_adjacent_into_openSet(self, node):
self.openSet.pop(node.point)
self.closeSet[node.point] = node
adjacentNodeList = []
# 对自己左上角周边8个点进行处理,如果物体能运动到新的位置,那么就添加为邻接点
for i in [0, -1, 1]:
for j in [0, -1, 1]:
if i == 0 and j == 0:
continue
_adjacent = (node.point[0] + i, node.point[1] + j)
if self.adjacent_is_through(_adjacent):
adjacentNodeList.append(Node(_adjacent, self.target, node))
# 检查每一个相邻的点
# 如果斜向运动, gCost 设为14, 非斜向运动设置为 10
for adjacent in adjacentNodeList:
# 如果邻接点是终点,找到路径。
if adjacent.point == self.target:
gCost = node.gCost + adjacent.get_gCost(node.point)
self.targetNode.reset_father(node, gCost)
return True
if adjacent.point in self.closeSet.keys():
continue
# 如果邻接点不在开放列表中,那么添加到开放列表中
if adjacent.point not in self.openSet.keys():
self.openSet[adjacent.point] = adjacent
# 如果已经在开放列表中,那么通过 gCost判断这个点是否更近
else:
existNode = self.openSet[adjacent.point]
if node.gCost + existNode.get_gCost(node.point) < existNode.gCost:
existNode.reset_father(node, node.gCost + existNode.get_gCost(node.point))
return False
# 精灵调用looking_for_path() 后直接可以通过 self.path 获得最终路径
def find_my_path(self):
# 将起点加入到 openset
self.openSet[self.start] = self.startNode
node = self.startNode
try:
while not self.add_adjacent_into_openSet(node):
node = self.find_min_fCost_node()
except BaseException as err:
# 路径找不到
print("No path from {} to {} with error: {}".format(self.start, self.target, err))
return False
return True
上面时传统的A-Star算法,在add_adjacent_into_openSet方法中使用了 adjacent_is_through()来判断是否该邻接点时可通过的。典型的判断方法是 是否改点是障碍物。为了解决大物体的寻路,只需要增加寻路过程中对邻接点的资格审查就可以了。
# 这样可以对任何尺寸的运动物体寻路
def adjacent_is_through(self, adjacent):
# 判断运动物体移动到邻接点时所占用的区域是否出界,先判断左上角
if not is_in_rect(adjacent, (0, 0), (GRID_X_QTY - 1, GRID_Y_QTY - 1)):
return False
# 如果运动物体超过一个格栅,判断右下角是否出界
if self.size > 1:
if not is_in_rect((adjacent[0] + self.size - 1, adjacent[1] + self.size - 1),
(0, 0), (GRID_X_QTY - 1, GRID_Y_QTY - 1)):
return False
# 运动物体移动过到邻接点时所占用的区域有没有障碍物
for i in range(0, self.size):
if OBSTRUCT in self.grids[adjacent[1] + i][adjacent[0]: adjacent[0] + self.size]:
return False
return True
# 如果给定的目的地不是一个合格的邻接点(不可达),那么调整目的地位置,找一个离当前目的地最近可可达点
def adjust_position(self, position):
if self.adjacent_is_through(position):
return position
_newPosition = position
_distance = 9999
# 调整范围可以设置为常量,大小根据实际情况设置就可以了。
for i in range(-5, 6):
for j in range(-4, 5):
if i == 0 and j == 0:
continue
if self.adjacent_is_through((position[0] + i, position[1] + j)):
if abs(i) + abs(j) < _distance:
_newPosition = (position[0] + i, position[1] + j)
_distance = abs(i) + abs(j)
if _newPosition != position:
print("Adjust position from {} to {}".format(position, _newPosition))
return _newPosition
raise Exception("I can't adjust the position!")
def find_my_path(self):
# 将起点加入到 openset
self.openSet[self.start] = self.startNode
node = self.startNode
try:
while not self.add_adjacent_into_openSet(node):
node = self.find_min_fCost_node()
except BaseException as err:
# 路径找不到
print("No path from {} to {} with error: {}".format(self.start, self.target, err))
return False
return True
上面已经找到路径了,下面需要将路径整理出来。
def mark_path(self):
# 只有startNode的父节点为None。 这里从目标节点回溯直到起始节点,路径包含起点。
# 由于是回溯,使用append还需使用 reverse 来反序,因此直接用 insert,插入到列表的最前端,不需要再反序。两种方法都可以。
self.path.clear()
# 将目的节点放在路径中
node = self.targetNode
self.path.insert(0, node.point)
# 根据下一个节点的位置
while node.father is not None:
self.path.insert(0, node.father.point)
node = node.father
mark_path()方法将路径经过的所有节点(节点之间的距离最大为一个格栅),但是路径中如果一个方向上超过一个格栅距离呢?那么去掉直线子路径中的中间节点,只保留拐弯点就可以了。下面的方法将路径简化。
def get_simplified_path(self):
assert self.path.__len__() >= 2
if self.path.__len__() == 2:
return
nodesCount = self.path.__len__()
tobeRemoved = []
for m in range(2, nodesCount):
# 如果相邻的三个节点在一条直线上,去掉中间节点
if self.path[m][0] - self.path[m - 1][0] == self.path[m - 1][0] - self.path[m - 2][0] \
and self.path[m][1] - self.path[m - 1][1] == self.path[m - 1][1] - self.path[m - 2][1]:
tobeRemoved.insert(0, m-1)
for m in tobeRemoved:
self.path.pop(m)
上面基本完成了A-Star的类封装,精灵使用AStar时,尽可能少的知道类的内部实现,提供一个方法给外部调用就好了。
def get_path(self):
if self.find_my_path():
self.mark_path()
self.get_simplified_path()
self.init_set()
return True
return False
好了,AStar类的实现就是这样了,外面这么调用。如果精灵寻路:
aStarPath = AStar(myGrids.grids, start, self.target, self.size)
if aStarPath.get_path():
self.path = aStarPath.path.copy()
上面AStar的第一个参数是格栅,那么格栅呢?
class Grids:
def __init__(self):
self.map = myMap
self.grids = [[1] * GRID_X_QTY for i in range(GRID_Y_QTY)]
# 根据障碍精灵产生矩阵
def create_grids_from_map(self):
for sp in self.map.elements:
# 先计算该障碍物的起始位置
row = sp.rect.top // GRID_HEIGHT
col = sp.rect.left // GRID_WIDTH
# 根据障碍物的大小修改格栅
for i in range(sp.rect[3] // GRID_HEIGHT):
for j in range(sp.rect[2] // GRID_WIDTH):
if col + j < GRID_X_QTY and row + i < GRID_Y_QTY:
self.grids[row + i][col + j] = OBSTRUCT
myGrids = Grids()
格栅是基于地图的,myMap就是你创建的地图,上一篇文章中已经实现了。Grids类只是将地图抽象化为格栅。
myGrids = Grids() 只是实现最简单的单例类实现,如果游戏中多有的山川河流阁楼对所有精灵都是对等的,也就是都是障碍物,那么整个游戏只需要一个Grids对象了。对于一些大一点的游戏,比如人不能在河里走,但是船可以,那么就不能用单例模式了,需要对同一张地图,不同类型的精灵实现不同的格栅了,这时候需要在地图元素Element上再增加一个属性来区分对某个或某些精灵是否为障碍物了。有兴趣的朋友可以进一步实现。
另外,仔细观察上面的路径图片的朋友可能发现,有一些斜线路径视乎穿过了障碍物的一个小角。其实这不是问题,只是本文简化了处理,格栅点代表一个格栅是否为障碍物,可以将格栅的中心作为格栅点,那么实际上精灵的左上角在格栅点位置的右上方。当然,如果你不希望这样,只需要更严格的限制,需要进一步审查邻接点的资格,也就是adjacent_is_through()方法就可以了。
本格栅大小为20px,GRID_X_QTY/GRID_Y_QTY 分别为60/40。小精灵与单个格栅大小相同,大精灵为4个格栅大小的正方形。对于长方形精灵,比如车辆,那么寻路算法时可以设置为大小为长边的正方形格栅,处理动画时设计好相关spritesheet表就可以。
下一篇将基于AStar算法,给出精灵寻路中的动画效果。遇到敌人时的处理、英雄自动寻敌、敌人自动行走等一些列的处理。
本人初学python,望请大家批评指正。谢谢!