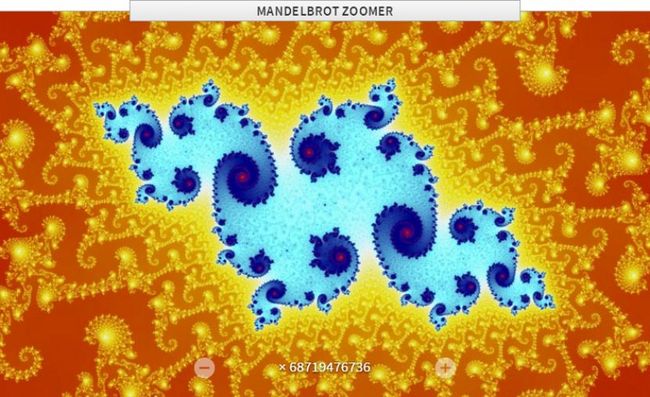
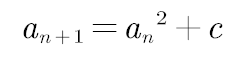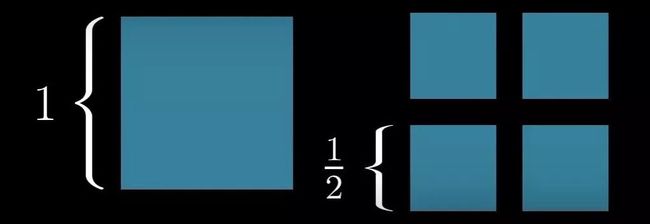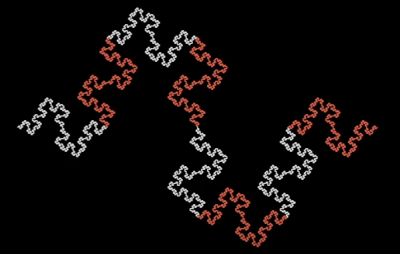令人目眩的万花筒,螺旋纹路的西兰花,它们之间存在什么相似之处?
我们说“一花一世界,一树一菩提”,说的是以小见大,从细微之处洞察宏观的哲学思考,而“一即是全,全即是一”,是我能想到的对分形最传神的表达。无数自然景物中都存在这样一个特点,你越是仔细去看,放大观察,就能发现越多的细节,放大镜下的世界,不仅没有变得单调乏味,反而显现出和正常尺度下相似的复杂性。想一想,如果有这么一样东西,不管你怎么放大它,看到的都是相似图案的循环,在放大10000倍的一个角落里,居然出现了和整个物体相同的花纹,这是多么美妙的图案!实际上,这就是完美分形的概念。
分形(Fractal)和物体的自相似性有很大联系。生活里面,我们发现许多自然生成的东西往往有极其复杂的细节,而且组成它们的微小部分就好像是整体的缩小版,它们在各个尺度上的复杂程度都很相似。蜿蜒的海岸线,发散的树枝,海螺的断面,这些都是自然生成的自相似图形,它们可能还不那么完美,但是一旦我们进入到理想世界,就可以构造出各种各样的完美分形。
数学里的分形
数学里的分形可以说是从康托尔集(Cantor Set)开始的。取一个线段,把它中间的1/3去掉得到两个分开的线段,再对剩下的两段进行相同的操作,得到4个线段,这样重复进行下去直到无穷,最后得到的图形集合就是康托尔集。
这样我们就用一个看似简单的步骤得到了一个无限复杂的图形,而且它的每一个细节放大之后都和整体看起来一样,这不是很神奇很有趣的一件事吗!
类似地,我们来看看科克曲线(Koch snowflake)的构造过程。从一个正三角形开始,在它的每个边上增加一个1/3大小的小三角,它就变成了一个六角星,接着在每个小三角的边上继续增加它的1/3大小的小三角,然后一直重复这个过程。
如果说康托尔集只是最平淡的分形作品,那么科克曲线终于让我们领略到了分形之美,总体看来它是一个雪花的形状,放大之后,你会发现它的细节就是本身形状的无数次复制,没有穷尽。聪明的你一定也发现了,这样一个图案会有非常奇怪的特性:它的周长是无限大,面积却不可能超过六角星的外接圆,它是一个无限复杂的封闭曲线,但绝不会和自己相交。
基于这些特性,著名数学家Mandelbrot联想到了一个困扰了人们很多年的问题:英国的海岸线究竟有多长?以此为题,他在科学杂志上发表了对这一问题的深入探讨,我们之所以测不准海岸线的长度,是因为海岸线就是一个天然的分形,你测量的尺子越精细,得到的长度就会越长,随着放大倍数的增大,海岸线呈现出来的细节也就越多。
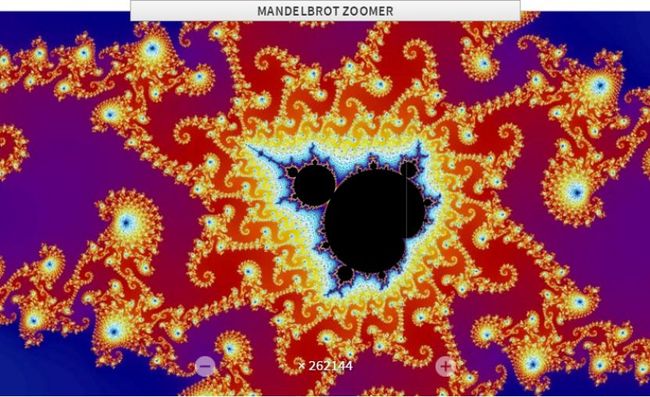
最后我们来看一看这个以他的名字命名的Mandelbrot集合,这个集合在平面上绘制出来就是一个奇异的分型图案,它集非常简单的产生公式和无限复杂的图像为一体,是的,它就是这样的一个怪物,所以曾被人们誉为“上帝的指纹”。
这一集合的产生是在一个二维平面内,具体来说是x轴是正常实数,y轴是对应复数的复平面。得到它的步骤是:
在平面内任取一点,例如(x,y)
让c=x+y
从a1=0开始循环计算这样一个式子:
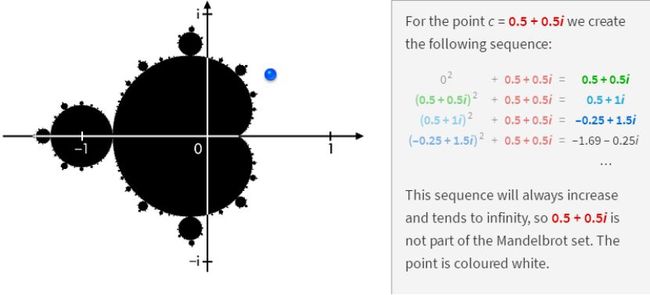
如果这个式子构成的数列是发散的,即最后趋近于无穷,那么这个点(x,y)不在Mandelbrot集合之内;反之,如果这个数列是有边界的,那么这个点在集合之内。
如果根据这个规则,我们把平面内的所有的点都验证一遍,就会画出Mandelbrot集合这个图案,它本身的细节极其复杂,以至于放大了百亿倍之后还呈现出精细的图案,每一个细节又和整体极其相似。
在这一图像刚刚被发现的时候,人们还不能看清它的精细结构,有大量数学家对这一发现表示不屑,他们认为分形没有实际用途,甚至不应该属于数学这一门类。但是很快,随着电脑技术的兴起,分形被广泛运用到复杂图像的产生和处理上,其中包括大量电影里的星球表面,山川起伏和液体喷射的画面。
工程学上,我们很早就发现了它在天线设计领域的重要性,使用分形样式的天线,不仅可以大大缩小天线的体积,还可以保证更好的收发效果,也正是因为分形的这一应用,我们的手机才得以摆脱那些明显的天线,做成现在这种简约时尚的样式。到现在,几乎所有的复杂工程建模里都可以看到分形的身影了。
分形的维度
既然是维度探索,那么我们就来谈谈分形和维度之间的巧妙联系吧。在上一篇维度探索中(维度探索:四维空间和更高维度),我们讨论了从0维到多维的世界,以及降维观察一个高维度物体的办法,但是提及的维度都是不小于0的整数维度,那么存不存在不是整数的维度呢?从数学的角度来说,答案是肯定的。
首先我们来看看一个有趣的图案,它的名字叫皮亚诺曲线(Peano Curve),它是通过不断构造这种自相似的形状最终把正方形填满的一种曲线。
如果这样一条本该是一维的曲线却凭借分形特征填满了二维的形状,那它到底是一维还是二维呢?
为了解决类似这样的问题,我们需要了解一下分形维度,它的神奇之处在于,这种定义下的维度可以是分数,也可以是无理数。也就是说存在这样的分形,它的维度是log2(3),或者是1.58。
想知道这是怎么做到的,我们要先玩一个找规律的游戏,以经典的谢尔宾斯基三角形(Sierpinski triangle)为例,来看看所谓分形维度是怎么确定的吧:
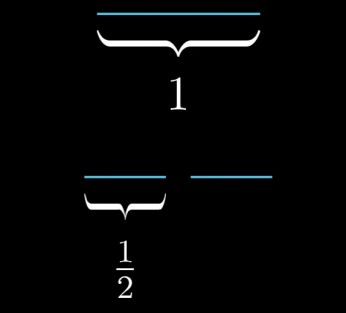
1,我们找到一个长度为1的线段,再把它的尺寸缩小成原来的0.5倍,那么要2个新的线段才能组成原来的线段。
2,接着找到一个面积为1的正方形,把它的尺寸(边长)缩小成原来的0.5倍,那么要4个新的正方形才能组成原来的正方形。
3,同样找到一个体积为1的正方体,把它的尺寸(边长)缩小成原来的0.5倍,那么要8个新的正方体才能组成原来的正方体。
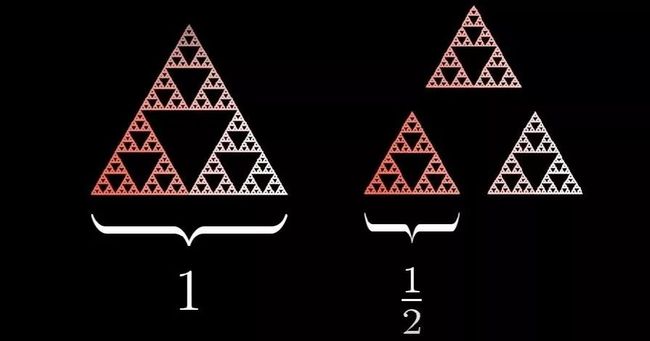
4,最后找到一个单位尺寸的谢尔宾斯基三角形,把它的尺寸(边长)缩小成原来的0.5倍,那么要3个新的三角形才能组成原来的三角形。
关注上面出现的这几组数字,我们就能解开分形维度的秘密:
对于普通的线段,缩放倍数是0.5时,新线段就是原来的0.5倍长,由于0.51=0.5,所以我们说线段是1维的;再看看正方形,缩放倍数是0.5的时候,新正方形是原来的0.25倍大,由于0.52=0.25,所以我们说正方形是2维的;同样,正方体缩放倍数是0.5,小正方体只有原来的八分之一即0.125,而0.53=0.125,代表正方体为3维。(Tips:缩放倍数也可以不是0.5,如果取其他的倍数,对计算结果没有影响。)
有兴趣的小伙伴可以自行检验,谢尔宾斯基三角形的维度计算结果是1.585维,或者说是之前提到过的log2(3)维(即log0.5(1/3))。按照这样的定义,一个分形物体的维度就出现了无理数的情况,这是多么的神奇!
课后习题时间:对于下图这样一个分形(在矩形边上不断增加小矩形边得到的),它的分形维度又是多少呢?大家可以在留言里写下你的答案。
到这里我们就完成了对分形维度的认识,或者可以叫它的另一个名字:Hausdorff维度。它的提出不仅解决了这种特殊的维度计算,还和整数维度的形体吻合得很好,就像我们的例子里计算的那样,不得不说是一个伟大的发现了。其实,分形维度更主要的是用来形容形体的不规则程度,和我们一般理解的空间维度已经有所不同了,但还是会受到传统意义上整数维度的约束,表现为平面上的分形维度在1到2之间,当然也有立体的分形,它们的维度也会更高。
为了帮助理解这种不规则度的评价方法,点击原文可以进入一个神奇的网站(ipfs),里面列举了许多形体的分形维度。在这里我也找到了一些有趣的东西,例如西兰花的分形维度是2.66,而人体肺部达到了2.97,也就是说肺部的复杂程度比西兰花要高,但实际上在传统空间维度上来说,它们都是三维物体。
来源参考
https://ipfs.io/ipfs/QmXoypizjW3WknFiJnKLwHCnL72vedxjQkDDP1mXWo6uco/wiki/List_of_fractals_by_Hausdorff_dimension.html
https://mathigon.org/world/Fractals
https://mathigon.org/world/resources/Fractals/Fractals.pdf
https://www.youtube.com/watch?v=gB9n2gHsHN4
Video by PBS: Hunting the hidden dimension (2008)