有限状态机(Python)

　　有限状态机（Finite-state machine, FSM），又称有限状态自动机，简称状态机，是表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。FSM是一种算法思想，简单而言，有限状态机由一组状态、一个初始状态、输入和根据输入及现有状态转换为下一个状态的转换函数组成。现实世界中存在大量具有有限个状态的系统：钟表系统、电梯系统、交通信号灯系统、通信协议系统、正则表达式、硬件电路系统设计、软件工程，编译器等，有限状态机的概念就是来自于现实世界中的这些有限系统。

　　一般可以用状态图来对一个状态机进行精确地描述。大家请看这个可乐机的状态图 。

　　从图中就可以清楚地看到可乐机的运行过程，图中直观地表现了可乐机投入不同金额硬币时的情况以及几个处理步骤的各个状态和它们之间的转换关系，根据投入硬币的不同面值，对总金额进行计算，并对各种操作进行响应以完成一次购买。 状态机的动态结构使得其在通讯系统，数字协议处理系统，控制系统，用户界面等领域得到了广泛地应用。

• 有限状态机模型

有限状态机是一个五元组$M=\left(Q,\Sigma ,\delta ,q_0,F\right)$，其中：

$Q=\left\{q_0,q_1,\text{...},q_n\right\}$是有限状态集合。在任一确定的时刻，有限状态机只能处于一个确定的状态$q_i$；

$\Sigma =\left\{\sigma _1,\sigma _{2,\text{...},}\sigma _n\right\}$是有限输入字符集合。在任一确定的时刻，有限状态机只能接收一个确定的输入$\sigma_j$；

$\delta :Q\times \Sigma \rightarrow Q$是状态转移函数，在某一状态下，给定输入后有限状态机将转入状态迁移函数决定的一个新状态；

$q_0\in Q$是初始状态，有限状态机由此状态开始接收输入；

$F\subseteq Q$是最终状态集合，有限状态机在达到终态后不再接收输入。

• 有限状态机的实现

　　有限状态机有多种实现方式：

　　1. switch-case或if-else

　　游戏引擎是有限状态机最为成功的应用领域之一，由于设计良好的状态机能够被用来取代部分的人工智能算法，因此游戏中的每个角色或者器件都有可能内嵌一个状态机。考虑RPG游戏中城门这样一个简单的对象，它具有打开（Opened）、关闭（Closed）、上锁（Locked）、解锁（Unlocked）四种状态。当玩家到达一个处于状态Locked的门时，如果此时他已经找到了用来开门的钥匙，那么他就可以利用它将门的当前状态转变为Unlocked，进一步还可以通过旋转门上的把手将其状态转变为Opened，从而成功地进入城内。

switch (state)  {
  // 处理状态Opened的分支
  case (Opened): {
    // 执行动作Open
    open();
    // 检查是否有CloseDoor事件
    if (closeDoor()) { 
      // 当前状态转换为Closed
      changeState(Closed)
    }
    break;
  } 
  // 处理状态Closed的分支
  case (Closed): {
    // 执行动作Close
    close();
    // 检查是否有OpenDoor事件
    if (openDoor()) {
      // 当前状态转换为Opened
      changeState(Opened);
    }
    // 检查是否有LockDoor事件
    if (lockDoor()) {
      // 当前状态转换为Locked
      changeState(Locked);
    }
    break;
  }
 
  // 处理状态Locked的分支
  case (Locked): {
    // 执行动作Lock
    lock();
    // 检查是否有UnlockDoor事件
    if (unlockDoor()) {
      // 当前状态转换为Unlocked
      changeState(Unlocked);
    }
    break;
  }
 
  // 处理状态Unlocked的分支
  case (Unlocked): {
    // 执行动作Unlock
    unlock();
    // 检查是否有LockDoor事件
    if (lockDoor()) {
      // 当前状态转换为Locked    
      changeState(Locked)
    }
    // 检查是否有OpenDoor事件    
    if (openDoor()) {
      // 当前状态转换为Opened
      changeSate(Opened);
    }
    break;
  } 
}

View Code

　　当状态量少并且各个状态之间变化的逻辑比较简单时，使用switch语句实现的有限状态机的确能够很好地工作，但代码的可读性并不十分理想。在很长一段时期内，使用switch语句一直是实现有限状态机的唯一方法，甚至像编译器这样复杂的软件系统，大部分也都直接采用这种实现方式。但之后随着状态机应用的逐渐深入，构造出来的状态机越来越复杂，这种方法也开始面临各种严峻的考验，其中最令人头痛的是如果状态机中的状态非常多，或者状态之间的转换关系异常复杂，那么简单地使用switch语句构造出来的状态机将难以扩展和维护。

　　2. 状态表

　　维护一个二维状态表，横坐标表示当前状态，纵坐标表示输入，表中一个元素存储下一个状态和对应的操作。这一招易于维护，但是运行时间和存储空间的代价较大。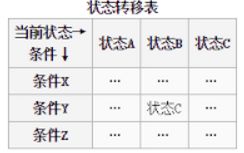

　　3. 使用宏定义描述状态机

　　4. 面向对象的设计模式

　　一个简单的例子：我们想识别一句只包含有限个词语的话表达的语气。句子以"Python is"开头，后面接着一个形容词或是加not限定的形容词。例如，

"Python is great"     → positive meaning
"Python is stupid"    → negative meaning
"Python is not ugly" → positive meaning

 　　首先定义一个StateMachine类

class StateMachine:
    def __init__(self): 
        self.handlers = {}        # 状态转移函数字典
        self.startState = None    # 初始状态
        self.endStates = []       # 最终状态集合
    
    # 参数name为状态名,handler为状态转移函数,end_state表明是否为最终状态
    def add_state(self, name, handler, end_state=0):
        name = name.upper() # 转换为大写
        self.handlers[name] = handler
        if end_state:
            self.endStates.append(name)

    def set_start(self, name):
        self.startState = name.upper()

    def run(self, cargo):
        try:
            handler = self.handlers[self.startState]
        except:
            raise InitializationError("must call .set_start() before .run()")
        if not self.endStates:
            raise  InitializationError("at least one state must be an end_state")
        
        # 从Start状态开始进行处理
        while True: 
            (newState, cargo) = handler(cargo)     # 经过状态转移函数变换到新状态
            if newState.upper() in self.endStates: # 如果跳到终止状态,则打印状态并结束循环
                print("reached ", newState)
                break 
            else:                        # 否则将转移函数切换为新状态下的转移函数 
                handler = self.handlers[newState.upper()]   

　　然后自定义有限状态和状态转移函数，并在main函数中开始进行处理：

from statemachine import StateMachine

# 有限状态集合
positive_adjectives = ["great","super", "fun", "entertaining", "easy"]
negative_adjectives = ["boring", "difficult", "ugly", "bad"]

# 自定义状态转变函数
def start_transitions(txt):
    # 过指定分隔符对字符串进行切片,默认为空格分割,参数num指定分割次数
    # 将"Python is XXX"语句分割为"Python"和之后的"is XXX"
    splitted_txt = txt.split(None, 1)  
    word, txt = splitted_txt if len(splitted_txt) > 1 else (txt,"")
    if word == "Python":   
        newState = "Python_state" # 如果第一个词是Python则可转换到"Python状态"
    else:
        newState = "error_state"  # 如果第一个词不是Python则进入终止状态
    return (newState, txt)        # 返回新状态和余下的语句txt

def python_state_transitions(txt):
    splitted_txt = txt.split(None,1)
    word, txt = splitted_txt if len(splitted_txt) > 1 else (txt,"")
    if word == "is":
        newState = "is_state"
    else:
        newState = "error_state"
    return (newState, txt)

def is_state_transitions(txt):
    splitted_txt = txt.split(None,1)
    word, txt = splitted_txt if len(splitted_txt) > 1 else (txt,"")
    if word == "not":
        newState = "not_state"
    elif word in positive_adjectives:
        newState = "pos_state"
    elif word in negative_adjectives:
        newState = "neg_state"
    else:
        newState = "error_state"
    return (newState, txt)

def not_state_transitions(txt):
    splitted_txt = txt.split(None,1)
    word, txt = splitted_txt if len(splitted_txt) > 1 else (txt,"")
    if word in positive_adjectives:
        newState = "neg_state"
    elif word in negative_adjectives:
        newState = "pos_state"
    else:
        newState = "error_state"
    return (newState, txt)



if __name__== "__main__":
    m = StateMachine()
    m.add_state("Start", start_transitions)      # 添加初始状态
    m.add_state("Python_state", python_state_transitions)
    m.add_state("is_state", is_state_transitions)
    m.add_state("not_state", not_state_transitions)
    m.add_state("neg_state", None, end_state=1)  # 添加最终状态
    m.add_state("pos_state", None, end_state=1)
    m.add_state("error_state", None, end_state=1)
    
    m.set_start("Start") # 设置开始状态
    m.run("Python is great")
    m.run("Python is not fun")
    m.run("Perl is ugly")
    m.run("Pythoniseasy")

　　运行结果如下：

reached  pos_state
reached  neg_state
reached  error_state
reached  error_state

　　可以看到，这种有限状态机的写法，逻辑清晰，表达力强，有利于封装事件。一个对象的状态越多、发生的事件越多，就越适合采用有限状态机的写法。

•  transitions开源库

　　transitions是一个由Python实现的轻量级的、面向对象的有限状态机框架。transitions最基本的用法如下，先自定义一个类，然后定义一系列状态和状态转移（定义状态和状态转移有多种方式，下面只写了最简明的一种，具体要参考文档说明），最后初始化状态机。

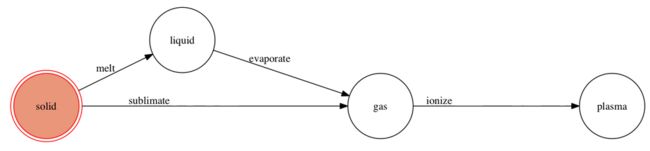
from transitions import Machine

# 定义一个自己的类
class Matter(object):
    pass
model = Matter()


# 状态定义
states=['solid', 'liquid', 'gas', 'plasma']


# 定义状态转移
# The trigger argument defines the name of the new triggering method
transitions = [
    {'trigger': 'melt', 'source': 'solid', 'dest': 'liquid' },
    {'trigger': 'evaporate', 'source': 'liquid', 'dest': 'gas'},
    {'trigger': 'sublimate', 'source': 'solid', 'dest': 'gas'},
    {'trigger': 'ionize', 'source': 'gas', 'dest': 'plasma'}]


# 初始化
machine = Machine(model=model, states=states, transitions=transitions, initial='solid')


# Test 
model.state    # solid

# 状体转变
model.melt()

model.state   # liquid

 

 

参考：

http://blog.csdn.net/xgbing/article/details/2784127

http://blog.csdn.net/gzlaiyonghao/article/details/1510688

http://www.python-course.eu/finite_state_machine.php

https://wiki.python.org/moin/FiniteStateMachine

http://fsme.sourceforge.net/

https://github.com/tyarkoni/transitions