（数据结构）稀疏矩阵三元组的存储结构及其基本算法设计

实验内容

1.假设n*n的稀疏矩阵A采用三元组表示，设计一个程序ex6-1.cpp，实现如下功能：
（1） 生成如下两个稀疏矩阵的三元组a和b。
{ 1 0 3 0 {3 0 0 0
0 1 0 0 0 4 0 0
0 0 1 0 0 0 1 0
0 0 1 1} 0 0 0 2}
（2）输出a转置矩阵的三元组
（3）输出a+b的三元组
（4）输出axb的三元组
2.设计一个算法，计算一个用三元组表表示的稀疏矩阵的对角线元素之和
3.设计一个算法Same（g1,g2）,判断两个广义g1和g2是否相同

代码实现

1、
exp6-1.cpp

#include
#define N 4
typedef int ElemType;
#define MaxSize 100/*矩阵非零元素最多个数*/
typedef struct
{
 int r;/*行号*/
 int c;/*列号*/
 ElemType d;/*元素值*/
}TupNode;/*三元组定义*/
typedef struct
{
 int rows;/*行数值*/
 int cols;/*列数值*/
 int nums;/*非零元素个数*/
 TupNode data[MaxSize];
}TSMatrix;/*三元组的存储结构*/
void CreatMat(TSMatrix &t,ElemType A[N][N])/*不生稀疏矩阵A的三元组表示*/
{
 int i,j;
 t.rows=N;t.cols=N;t.nums=0;
 for(i=0;ib.data[j].c)/*a元素的列号大于b元素的列号*/
   {
    c.data[k].r=b.data[i].r;/*将b元素添加到c中*/
    c.data[k].c=b.data[i].c;
    c.data[k].d=b.data[i].d;
    k++;j++;
   }
   else /*a元素的列号等于b元素的序号*/
   {
    v=a.data[i].d+b.data[j].d;
    if(v!=0)/*只将不为0的结点添加c中*/
    {
     c.data[k].r=a.data[i].r;
     c.data[k].c=a.data[i].c;
     c.data[k].d=v;
    }
    i++;j++;
   }
  }
  else if(a.data[i].r

结果截图：

2、

#include
using namespace std;
#define N 4
#define MaxSize 100
typedef int ElemType;
typedef struct
{
	int r;//行号
	int c;//列号
	ElemType d;//元素值
}TupNode;//三元组定义
typedef struct
{
	int rows;//行数
	int cols;//列数
	int nums;//非零元素个数
	TupNode data[MaxSize];
}TSMatrix;//三元组顺序表定义
		  //产生稀疏矩阵A的三元组表示t
void CreatMat(TSMatrix &t, ElemType A[N][N])
{
	int i, j;
	t.rows = N;
	t.cols = N;
	t.nums = 0;
	for (i = 0; i < N; i++)
	{
		for (j = 0; j < N; j++)
		{
			if (A[i][j] != 0)
			{
				t.data[t.nums].r = i;
				t.data[t.nums].c = j;
				t.data[t.nums].d = A[i][j];
				t.nums++;
			}
		}
	}
}
//输出三元组表示t
void DispMat(TSMatrix t)
{
	int i;
	if (t.nums <= 0)
		return;
	else
		printf("\t%d\t%d\t%d\n", t.rows, t.cols, t.nums);
	printf("\t---------------------------\n");

	for (i = 0; i < t.nums; i++)
	{
		printf("\t%d\t%d\t%d\n", t.data[i].r, t.data[i].c, t.data[i].d);
	}

}
bool diagonal(TSMatrix a, ElemType &sum)
{
	sum = 0;
	if (a.rows != a.cols)
	{
		printf("不是对角矩阵\n");
		return false;
	}
	for (int i = 0; i < a.nums; i++)
	{
		if (a.data[i].r == a.data[i].c)
			sum += a.data[i].d;
	}
	return true;
}
int main()
{
	ElemType sum,A[N][N] = { {1,0,0,0},{0,3,0,5},{0,0,5,0},{0,0,0,7} };
	TSMatrix a;
	CreatMat(a, A);
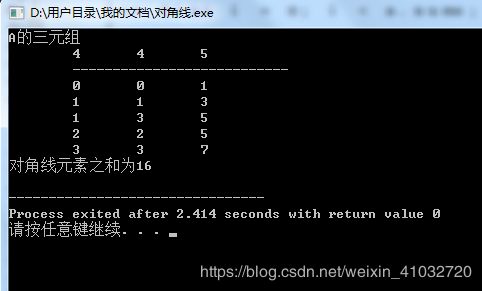
	printf("A的三元组\n");
	DispMat(a);
	diagonal(a, sum);
	printf("对角线元素之和为%d\n", sum);
	return 0;
}

结果截图：

3、

#include
using namespace std;
typedef struct lnode
{
	int tag;//结点类型标识
	union
	{
		char data;
		struct lnode *sublist;
	}val;
	struct lnode *link;//指向下一个元素
}GLNode;//声明广义表结点类型
//返回由括号表示法表示s的广义表连式存储结构
GLNode *CreateGL(const char * &s)
{
	GLNode *g;
    char ch = * s++;//取一个字符
	if (ch != '\0')//串未结束判断
	{
		g = (GLNode *)malloc(sizeof(GLNode));
		if (ch == '(')
		{
			g->tag = 1;
			g->val.sublist = CreateGL(s);
		}
		else if (ch == ')')
			g = NULL;
		else if (ch == '#')
			g->val.sublist = NULL;
		else
		{
			g->tag = 0;
			g->val.data = ch;
		}

	}
	else
		g = NULL;
	ch = * s++;
	if (g != NULL)
	{
		if (ch == ',')
			g->link = CreateGL(s);
		else
			g->link = NULL;
	}
	return g;
}
//输出广义表g
void DispGL(GLNode *g)
{
	if (g != NULL)
	{
		if (g->tag == 0)
			cout << g->val.data;
		else
		{
			cout << "(";
			if (g->val.sublist == NULL)
				cout << "#";
			else
				DispGL(g->val.sublist);
			cout << ")";
		}
		if (g->link != NULL)
		{
			cout << ",";
			DispGL(g->link);
		}
	}
}
//销毁广义表g
void DestroyGL(GLNode * &g)
{
	GLNode *g1, *g2;
	g1 = g->val.sublist;
	while (g1 != NULL)
	{
		if (g1->tag == 0)
		{
			g2 = g1->link;
			free(g1);
			g1 = g2;
		}
		else
		{
			g2 = g1->link;
			DestroyGL(g1);
			g1 = g2;
		}
	}
	free(g);
}
bool Same(GLNode *g1, GLNode *g2)
{
	if (g1 == NULL && g2 == NULL)
		return true;
	else if (g1 == NULL || g2 == NULL)
		return false;
	else
	{
		if (g1->tag == 0 && g2->tag == 0)
		{
			if (g1->val.data != g2->val.data)
				return false;
			return(Same(g1->link, g2->link));
		}
		else if (g1->tag == 1 && g2->tag == 1)
			return(Same(g1->val.sublist, g2->val.sublist))
			&Same(g1->link, g2->link);
		else
			return false;
	}
}
int main()
{
	GLNode  *g1, *g2;
	const char * str1 ="(b,(b,a,(#),d),((a,b),c,((,))))";
	const char * str2= "(b,(b,a,(#),d),((a,b),c,((#))))";
	g1 = CreateGL(str1);
	g2 = CreateGL(str2);
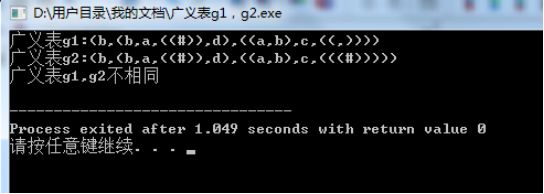
	cout << "广义表g1:";
	DispGL(g1);
	cout << endl;
	cout << "广义表g2:";
	DispGL(g2);
	cout << endl;
	if (Same(g1, g2))
	{
		cout << "广义表g1,g2相同" << endl;
	}
	else
		cout<< "广义表g1,g2不相同" << endl;
	DestroyGL(g1);
	DestroyGL(g2);
	return 0;
}

结果截图：