数据结构:Trie树(前缀树)原理及C++实现
前言:
最近学习了tire树(前缀树),也就是单词查找树;正如书上所言,这是人类对算法研究的最高成果之一,学会了后感觉尤为深刻,接下来就来记录下自己的感受。
原理:
Trie树和其他的数据结构一样,支持查找、插入以及删除操作,当然也可以添加其他的操作。Trie树的编程非常的简单,这一切都得益于其优秀的性质。Trie树和其他的各种查找树一样也是由链接的节点组成的数据结构,这些节点可以为空,也可以指向其他的节点。那么我们先看看节点的属性:
struct TreeNode {
Color color;
Position Next[R];
};
可以看见,节点只存储了两种元素,第一种是一个枚举型变量color,其存储的变量为Red和Black,也就是该节点的颜色;第二个元素是一个指向下一层节点的指针的数组,
这里是整个Trie树中唯一的一个不好的性质,为了达到O(logN)的时间复杂度,我们的Next必须要申请R个空间,其中R为字典中的字符数。并且注意的是,所有的非空节点都得申请这么多的空间,肯定有人会说,这样做的空间复杂度不是很高吗?没错,但这也正是我们所必须付出的代价。至于为什么需要这么做,我们会在具体的原理中看到原因。
具体结构:
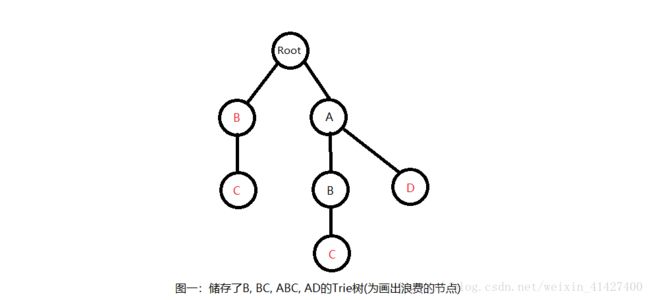
Trie树的结构非常简单,由一个根节点引出所有的节点,且根部不储存任何的属性。对于储存其中的单词,会依据索引来依次储存,如一个单词abc,那么根节点的Next中会有一个指向a,a的Next中会有一个指向b,最后b也会指向c,最后c节点的颜色会被标位红色,表示到c为止,有一个单词储存其中。(如图1所示)
查找操作:
查找操作非常的简单,从第一字符开始检索查找的单词,若第一个字符查找到,则从上一层查找到的节点检索其下一层是否有第二个字符,直到查找完最后一位字符;
若中途只能查找到空节点或是最后节点颜色为黑色,则返回false,否则返回true;
在图一中的Trie树中如果我们要查找单词ABC,那么我们会先在树根的下一层节点中检索A,检索到了A就再在其下一层检索B,最后检索到C,因为其颜色为Red,那么久返回true。
具体代码如下:
/* 查找函数:在TrieTree中查找对应的单词,并返回查找结果
* 参数:key:想要查找的单词
* 返回值:bool:TrieTree中有key返回true,否则返回false
*/
bool TrieTree::Find(string key) const {
// 查找key最后字符所在节点
Position P = Find(key, Root, 0);
// 无节点则返回false
if (P == NULL)
return false;
// 根据节点颜色返回
if (P->color == Red)
return true;
else
return false;
}
/* 查找驱动函数:在TrieTree中查找指定的单词并返回其最后的字符所在节点
* 参数:key:想要进行查找的单词,tree:当前递归查找的树节点,d:当前检索的索引
* 返回值:Position:单词最后字符所在的节点
*/
Position TrieTree::Find(string key, Position tree, int d) const {
// 节点不存在则返回空
if (tree == NULL)
return NULL;
// 若检索完成,返回该节点
if (d == key.length())
return tree;
// 检索下一层
char c = key[d];
return Find(key, tree->Next[c], d + 1);
}
插入操作:
插入操作也非常的简单,和查找相同,我们从根部开始向下一层检索,若碰到空节点,则生成一个新的节点,直到最后一个字符的节点也生成出来,并将最后一个节点标位红色。
接下来是具体代码:
/* 插入函数:向TrieTree中插入指定的单词
* 参数:key:想要进行插入的字符串
* 返回值:无
*/
void TrieTree::Insert(string key) {
// 从根节点开始递归插入
Insert(key, Root, 0);
}
/* 插入驱动函数:将指定的单词进行递归插入
* 参数:key:想要进行插入的单词,tree:当前递归节点,d:当前检索的字符索引
* 返回值:无
*/
void TrieTree::Insert(string key, Position &tree, int d) {
// 若没有节点则生成新节点
if (tree == NULL) {
tree = new TreeNode();
if (tree == NULL) {
cout << "新节点申请失败!" << endl;
return;
}
tree->color = Black;
for (int i = 0; i < R; i++)
tree->Next[i] = NULL;
}
// 若检索到最后一位,则改变节点颜色
if (d == key.length()) {
tree->color = Red;
return;
}
// 检索下一层节点
char c = key[d];
Insert(key, tree->Next[c], d + 1);
}
删除操作:
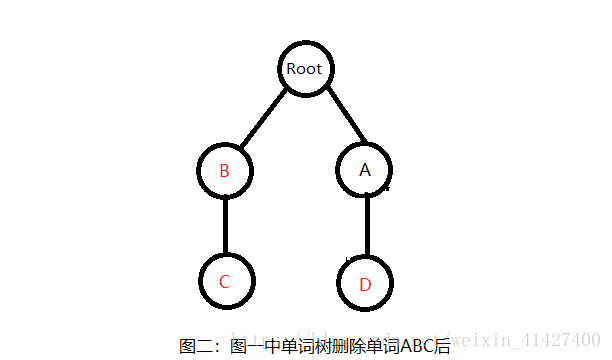
最后是删除操作,删除操作要稍微复杂一些。我们需要查找到目标单词的最后一个单词所在的节点,将这个单词的颜色标位黑色,同时从这个节点开始向根节点回溯,
如果一个节点的下一层节点全为空节点则删除该节点。(如图二所示)
具体代码如下:
/* 删除函数:删除TrieTree中的指定单词
* 参数:key:想要删除的指定元素
* 返回值:无
*/
void TrieTree::Delete(string key) {
// 从根节点开始递归删除
Delete(key, Root, 0);
}
/* 删除驱动函数:将指定单词进行递归删除
* 参数:key:想要进行删除的单词,tree:当前树节点,d:当前的索引下标
* 返回值:无
*/
void TrieTree::Delete(string key, Position &tree, int d) {
// 若未空树则返回
if (tree == NULL)
return;
// 检索到指定单词,将其颜色变黑
if (d == key.length())
tree->color = Black;
// 检索下一层节点
else {
char c = key[d];
Delete(key, tree->Next[c], d + 1);
}
// 红节点直接返回
if (tree->color == Red)
return;
// 若未黑节点,且无下层节点则删除该节点
for (int i = 0; i < R; i++)
if (tree->Next[i] != NULL)
return;
delete tree;
tree = NULL;
}C++实现:
还是先给出整个Tire树的完整代码吧,首先是.h文件:
#ifndef TRIETREE_H
#define TRIETREE_H
#include
#include
#include
using namespace std;
// 定义R为常量
const int R = 256;
// 重定义树节点,便于操作
typedef struct TreeNode *Position;
/* color枚举,储存元素:Red, Black*/
enum Color {Red, Black};
/* TrieTree节点
* 储存元素:
* coloe:节点颜色,红色代表有此单词,黑色代表没有
* Next:下一层次节点
*/
struct TreeNode {
Color color;
Position Next[R];
};
/* TrieTree类(前缀树)
* 接口:
* MakeEmpty:重置功能,重置整颗前缀树
* keys:获取功能,获取TrieTree中的所有单词,并储存在一个向量中
* Insert:插入功能,向单词树中插入新的单词
* Delete:删除功能,删除单词树的指定单词
* IsEmpty:空函数,判断单词树是否为空
* Find:查找函数,查找对应的单词,并返回查找情况:查找到返回true,否则返回false
* LongestPrefixOf:查找指定字符串的最长前缀单词;
* KeysWithPrefix:查找以指定字符串为前缀的单词;
* KeysThatMatch:查找匹配对应字符串形式的单词,"."表示任意单词
*/
class TrieTree
{
public:
// 构造函数
TrieTree();
// 析构函数
~TrieTree();
// 接口函数
void MakeEmpty();
vector keys();
void Insert(string);
void Delete(string);
bool IsEmpty();
bool Find(string) const;
string LongestPrefixOf(string) const;
vector KeysWithPrefix(string) const;
vector KeysThatMatch(string) const;
private:
// 辅助功能函数
void MakeEmpty(Position);
void Insert(string, Position &, int);
void Delete(string, Position &, int);
Position Find(string, Position, int) const;
int Search(string, Position, int, int) const;
void Collect(string, Position, vector &) const; // 对应KeysWithPrefix()
void Collect(string, string, Position, vector &) const; // 对应KeysThatMatch()
// 数据成员
Position Root; // 储存根节点
};
#endif
接着是.cpp文件:
#include "TrieTree.h"
/* 构造函数:初始化对象
* 参数:无
* 返回值:无
*/
TrieTree::TrieTree() {
Root = new TreeNode();
if (Root == NULL) {
cout << "TrieTree申请失败!" << endl;
return;
}
// 根节点为黑色节点
Root->color = Black;
for (int i = 0; i < R; i++)
Root->Next[i] = NULL;
}
/* 析构函数:对象消亡时回收储存空间
* 参数:无
* 返回值:无
*/
TrieTree::~TrieTree() {
MakeEmpty(Root); // 调用重置函数,从树根开始置空
}
/* 重置函数:重置TrieTree
* 参数:无
* 返回值:无
*/
void TrieTree::MakeEmpty() {
// 将根节点的下一层节点置空
for (char c = 0; c < R; c++)
if (Root->Next[c] != NULL)
MakeEmpty(Root->Next[c]);
}
/* 重置函数:重置指定节点
* 参数:tree:想要进行重置额节点
* 返回值:无
*/
void TrieTree::MakeEmpty(Position tree) {
// 置空下一层节点
for (char c = 0; c < R; c++)
if (tree->Next[c] != NULL)
MakeEmpty(tree->Next[c]);
// 删除当前节点
delete tree;
tree = NULL;
}
/* 获取函数:获单词树中的所有单词,并返回储存的向量
* 参数:无
* 返回值:vector:储存单词树中所有单词的向量
*/
vector TrieTree::keys() {
// 返回所有以""为前缀的单词,即所有单词
return KeysWithPrefix("");
}
/* 插入函数:向TrieTree中插入指定的单词
* 参数:key:想要进行插入的字符串
* 返回值:无
*/
void TrieTree::Insert(string key) {
// 从根节点开始递归插入
Insert(key, Root, 0);
}
/* 插入驱动函数:将指定的单词进行递归插入
* 参数:key:想要进行插入的单词,tree:当前递归节点,d:当前检索的字符索引
* 返回值:无
*/
void TrieTree::Insert(string key, Position &tree, int d) {
// 若没有节点则生成新节点
if (tree == NULL) {
tree = new TreeNode();
if (tree == NULL) {
cout << "新节点申请失败!" << endl;
return;
}
tree->color = Black;
for (int i = 0; i < R; i++)
tree->Next[i] = NULL;
}
// 若检索到最后一位,则改变节点颜色
if (d == key.length()) {
tree->color = Red;
return;
}
// 检索下一层节点
char c = key[d];
Insert(key, tree->Next[c], d + 1);
}
/* 删除函数:删除TrieTree中的指定单词
* 参数:key:想要删除的指定元素
* 返回值:无
*/
void TrieTree::Delete(string key) {
// 从根节点开始递归删除
Delete(key, Root, 0);
}
/* 删除驱动函数:将指定单词进行递归删除
* 参数:key:想要进行删除的单词,tree:当前树节点,d:当前的索引下标
* 返回值:无
*/
void TrieTree::Delete(string key, Position &tree, int d) {
// 若未空树则返回
if (tree == NULL)
return;
// 检索到指定单词,将其颜色变黑
if (d == key.length())
tree->color = Black;
// 检索下一层节点
else {
char c = key[d];
Delete(key, tree->Next[c], d + 1);
}
// 红节点直接返回
if (tree->color == Red)
return;
// 若未黑节点,且无下层节点则删除该节点
for (int i = 0; i < R; i++)
if (tree->Next[i] != NULL)
return;
delete tree;
tree = NULL;
}
/* 空函数:判断TrieTree是否为空
* 参数:无
* 返回值:bool:空树返回true,非空返回false
*/
bool TrieTree::IsEmpty() {
for (int i = 0; i < R; i++)
if (Root->Next[i] != NULL)
return false;
return true;
}
/* 查找函数:在TrieTree中查找对应的单词,并返回查找结果
* 参数:key:想要查找的单词
* 返回值:bool:TrieTree中有key返回true,否则返回false
*/
bool TrieTree::Find(string key) const {
// 查找key最后字符所在节点
Position P = Find(key, Root, 0);
// 无节点则返回false
if (P == NULL)
return false;
// 根据节点颜色返回
if (P->color == Red)
return true;
else
return false;
}
/* 查找驱动函数:在TrieTree中查找指定的单词并返回其最后的字符所在节点
* 参数:key:想要进行查找的单词,tree:当前递归查找的树节点,d:当前检索的索引
* 返回值:Position:单词最后字符所在的节点
*/
Position TrieTree::Find(string key, Position tree, int d) const {
// 节点不存在则返回空
if (tree == NULL)
return NULL;
// 若检索完成,返回该节点
if (d == key.length())
return tree;
// 检索下一层
char c = key[d];
return Find(key, tree->Next[c], d + 1);
}
/* 最长前缀驱动:获取最长前缀在指定字符串中的所有下标
* 参数:key:用于查找的字符串,tree:当前的递归节点,d:当前检索的索引,length:当前最长前缀的长度
* 返回值:int:最长前缀的长度
*/
int TrieTree::Search(string key, Position tree, int d, int length) const {
// 空树则返回当前前缀的长度
if (tree == NULL)
return length;
// 更新前缀长度
if (tree->color == Red)
length = d;
// 检索到末尾则返回长度
if (d == key.length())
return length;
// 检索下一层
char c = key[d];
return Search(key, tree->Next[c], d + 1, length);
}
/* 最长前缀函数:获取指定字符串中,在TrieTree中存在的最长前缀
* 参数:key:想要进行查找的字符串
* 返回值:string:最长的前缀单词
*/
string TrieTree::LongestPrefixOf(string key) const {
// 获取最长前缀的下标
int Length = Search(key, Root, 0, 0);
return key.substr(0, Length);
}
/* 前缀查找驱动:将当前层次所有符合前缀要求的单词存入向量
* 参数:key:指定的前缀,tree:当前的节点层次,V:用于储存的向量
* 返回值:无
*/
void TrieTree::Collect(string key, Position tree, vector &V) const{
// 空节点直接返回
if (tree == NULL)
return;
// 红节点则压入单词
if (tree->color == Red)
V.push_back(key);
// 检索下一层节点
for (char i = 0; i < R; i++)
Collect(key + i, tree->Next[i], V);
}
/* 前缀查找:查找TrieTree中所有以指定字符串为前缀的单词
* 参数:key:指定的前缀
* 返回值:vector:储存了所有目标单词的向量
*/
vector TrieTree::KeysWithPrefix(string key) const {
vector V;
// 搜集目标单词到向量V
Collect(key, Find(key, Root, 0), V);
return V;
}
/* 单词匹配驱动:搜集当前层次中所有匹配成功的单词
* 参数:pre:匹配前缀单词,pat:用于指定形式的字符串,tree:当前的检索层次,V:用于储存匹配成功单词的向量
* 返回值:无
*/
void TrieTree::Collect(string pre, string pat, Position tree, vector &V) const {
// 获取前缀的长度
int d = pre.length();
// 空树直接返回
if (tree == NULL)
return;
// 若前缀长度与指定单词相同且当前节点为红色,则压入前缀
if (d == pat.length() && tree->color == Red)
V.push_back(pre);
// 若只是长度相同直接返回
if (d == pat.length())
return;
// 检索下一层节点
char next = pat[d];
for (char c = 0; c < R; c++)
if (next == '.' || next == c)
Collect(pre + c, pat, tree->Next[c], V);
}
/* 单词匹配函数:搜集TrieTree中所以匹配指定字符串形式的单词
* 参数:pat:用于指定形式的字符串
* 返回值:vector:储存所有目标单词的向量
*/
vector TrieTree::KeysThatMatch(string pat) const {
vector V;
// 搜集所有匹配的单词到向量V
Collect("", pat, Root, V);
return V;
}
那么整个Trie树的实现就到这里结束了,如果有什么疑问欢迎留言大家一起讨论~~
参考文献:《算法——第四版》