PH525x series - Multi-Dimensional Scaling Plots

多维尺度分析（MDS）

在奇异值分解那一章节我们已将学过：

在此基础上，我们若假设的前两列的平方和远远大于其余列的平方和，换句话说若是对角线上的第个奇异值，那么：，那么我们便有：

的第列便约等于：

如果我们设等于：

那么：

也就是说，在这种情况下，样本和样本之间的距离就可以用两个二维的点进行约算了：

举例说明：

library(rafalib)
library(tissuesGeneExpression)
data(tissuesGeneExpression)
colind <- tissue %in% c("kidney","colon","liver")
mat <- e[,colind]
group <- factor(tissue[colind])

s <- svd(mat-rowMeans(mat))
PC1 <- s$d[1]*s$v[,1]
PC2 <- s$d[2]*s$v[,2]
mypar(1,1)
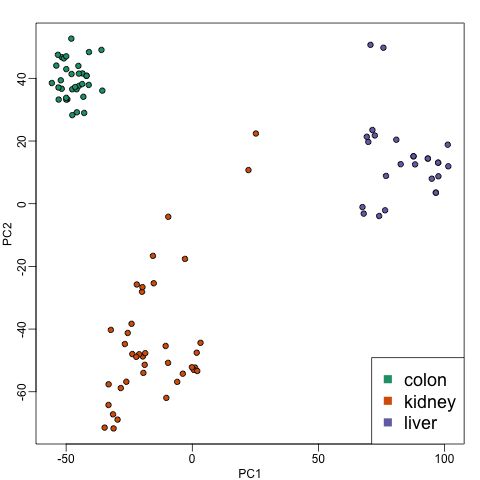
plot(PC1,PC2,pch=21,bg=as.numeric(group))
legend("bottomright",levels(group),col=seq(along=levels(group)),pch=15,cex=1.5)

201912161109.png

到这一趴的时候我头一开始特别没理解为啥在给这些点涂色的时候直接as.numeric(group)就行，后来想明白了，也就是奇异值分解得到的右奇异矩阵中的每一列（也就是每一个特征向量）中的元素顺序是与原始矩阵的样本顺序一致的。

从上图中我们可以看到单是用前两个维度就可以将这些样本很好的分开，再看下方差解释度的趋势图：

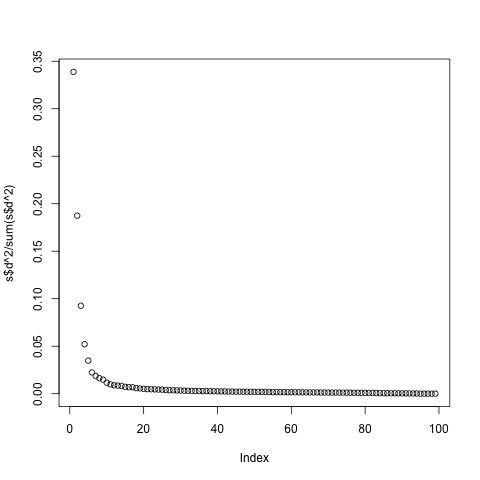
plot(s$d^2/sum(s$d^2))

201912161119.png

可以看到，其实前两个维度的方差解释度加起来也就50%多一些，也就说虽然有很多信息不能在图中展示出来，但是单是用前两个维度画图却仍能够很好的看出点与点之间的分布情况。

我们再看下用第3和第4个主成分做出的图：

PC3 <- s$d[3] * s$v[,3]
PC4 <- s$d[4] * s$v[,4]
mypar(1,1)
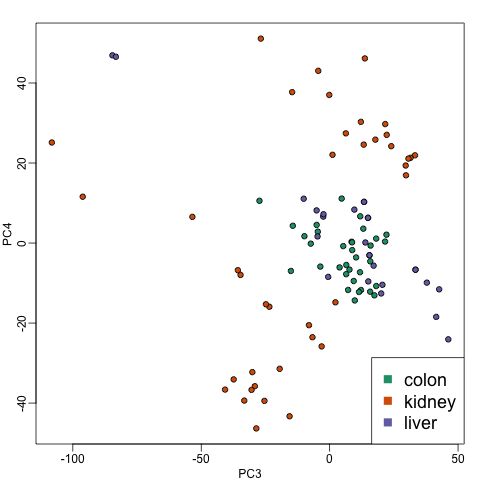
plot(PC3,PC4,pch=21,bg=as.numeric(group))
legend("bottomright",levels(group),col=seq(along=levels(group)),pch = 15,cex=1.5)

201912161314.png

在上图中，kidney组织的样本很明显的被分开了，这可能与后面要学的batch effects有关，更加详细的以后再说，关于这点作者在这里也就提了一句。

cmdscale

我们除了可以使用svd()函数画多维尺度图之外，还可以使用cmdscale()函数，它以一个距离矩阵作为输入参数，然后利用PCA为这一矩阵提供一个最近似的k维矩阵（k默认为2），与svd()相比，运算时间更短。

举例说明：

d <- dist(t(mat))
mds <- cmdscale(d)
mypar()
plot(mds[,1],mds[,2],bg=as.numeric(group),pch=21,
     xlab="First dimension",ylab="Second dimension")
legend("bottomleft",levels(group),col=seq(along=levels(group)),pch=15)

201912161330.png

符号问题

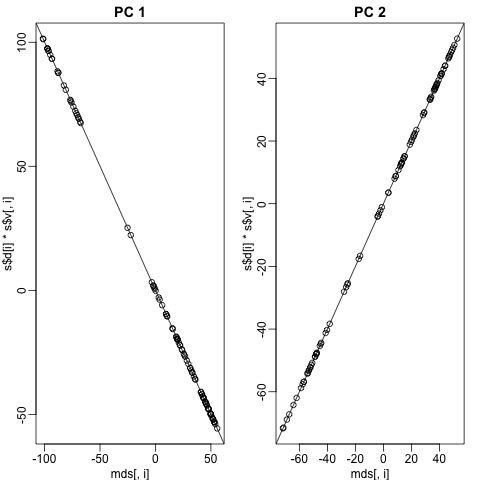
观察下图，可以看出这两种方法得到的第一第二主成分的正负符号并不完全一致：

mypar(1,2)
for (i in 1:2){
  plot(mds[,i],s$d[i]*s$v[,i],main=paste("PC",i))
  b <- ifelse(cor(mds[,i],s$v[,i])>0,1,-1)
  abline(0,b)
}

201912161332.png

这是因为奇异值分解的结果并不唯一，关键就在这正负符号上：

减去平均数的问题

如果你仔细看过文章内容，就会发现在我们之前奇异值分解的计算当中，都会先减去行均值，也就是用原始矩阵减去行均值得到的新矩阵计算距离与用原始矩阵去计算距离是一回事：

所以，为了减少计算量，我们通常都会这么去处理。

阅读原文请戳