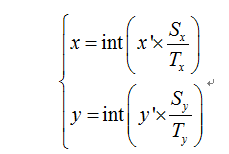卷积神经网络原理
目录
图像核与卷积
图像核的作用
卷积神经网络
卷积层
池化层
Flatten层
CNN的总体结构
网络的构造
网络的训练与Dropout正则化
图像核与卷积
我们知道,图像可以用矩阵表示。例如单通道图像可以用一个维度与图像尺寸相同的矩阵表示,三通道(彩色)图像可用三个这样的矩阵表示,四通道图像(包括透明度)......。
图像核是一个维度很小的矩阵,一般为3X3,5X5,9X9;有时候,将其视为一个移动的窗口比较方便
卷积运算是两个矩阵对应元素相乘后相加,假设有两个矩阵A,K,其卷积运算如下:
图像核的作用
图像核可以实现很多PS能够实现的功能,实际上,PS中的一些图像处理功能,如平滑处理(模糊处理)、锐化、边缘化等。
对于一张图像,图像核是如何作用的呢?
以3X3的图像核为例,假设有一个图像核(通过高斯函数产生)为:
对如下图像,对除边缘像素外的所有像素,找到他们的8个近邻像素,构成一个9x9的矩阵,与图像核K卷积,从而根据原始图像得到其输出:
上图中,左边的虚线构成的矩阵与K卷积,矩阵的中心元素为当前像素,当前像素的像素值即卷积的结果。
不同的图像核处理图像,可以得到不同的功能。上述的K可以实现图像的模糊处理,有时也叫平滑处理,它可以消除像素与像素之间的差异。通过调整图像核K,我们可以实现图像锐化、边缘检测、腐蚀、肥大化等功能,从而完成图像的特征提取。
卷积神经网络
卷积神经网络区别于BP网络,CNN中有些层的节点可以接收多个矩阵,而BP神经网络只能接收多个值。若用CNN处理三通道(彩色)图像,则CNN的输入层为三个节点,每个节点输出一个通道的矩阵。
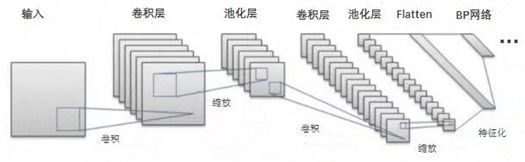
正因为卷积神经网络的输入、输出可以为矩阵,因此区别于BP等神经网络,它的网络结构除了输入、隐藏层、输出层外,还有卷积层、池化层和Flatten层。
卷积层
在CNN中,一般输入层之后就是卷积层。输入层读取并输出图像,以RGB图像为例,此时输入层输出三个矩阵,分别对应R、G、B三通道。这三个矩阵被卷积层所接收,并用节点的推向核滑动卷积。
在卷积层中,节点的图像核为网络的参数,由模型训练得出。卷积层中,一个节点的图像核等于上一层接收的矩阵数量。在本例中,卷积层的节点应有3个图像核。对于接收到的每一个矩阵,都有一个图像核与之对应。
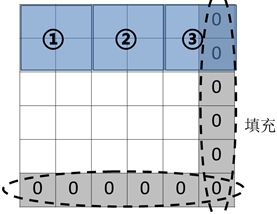
图像核此时作为一个窗口,在对应的矩阵中滑动卷积。但在滑动卷积过程中,可能会遇到“滑不完”的情况,如下图所示,假设图像核的尺寸为2X2,矩阵的大小为5X5,滑动的步长为2。很明显,在移动一步后,剩余最后一列无法匹配。此时,我们要对矩阵进行填充,以便图像核能够完全滑动。一般填充0元素。当然,步长为1时,就不会出现这样的情况。
节点的图像核在对应的输入矩阵中滑动卷积,输出的值与便宜项累加,得到净输出矩阵,如下所示: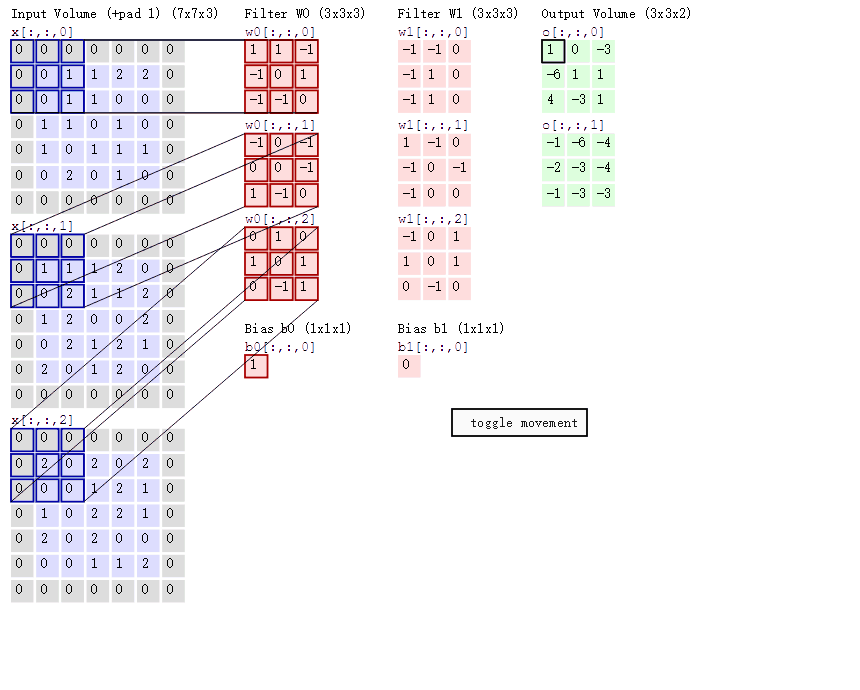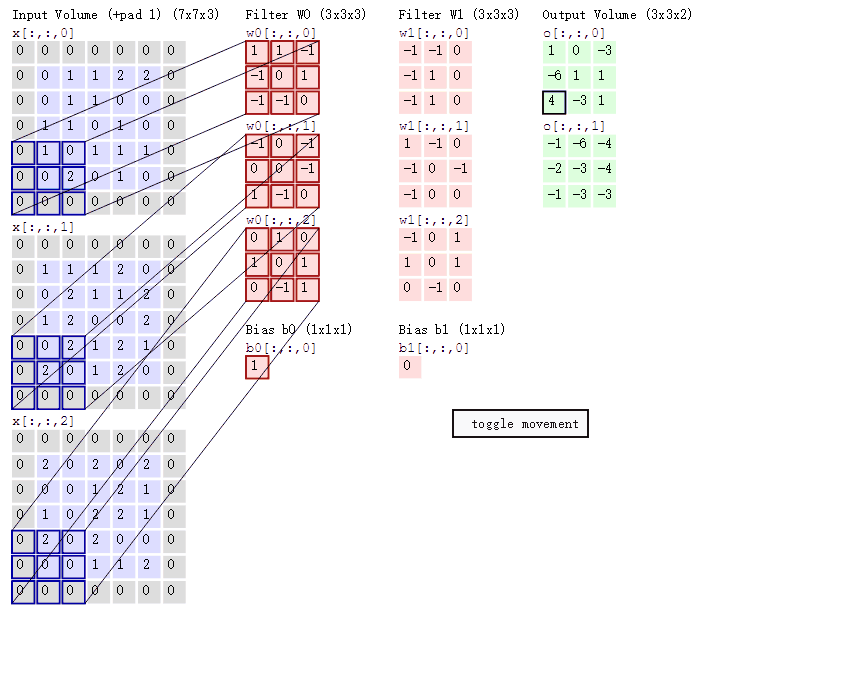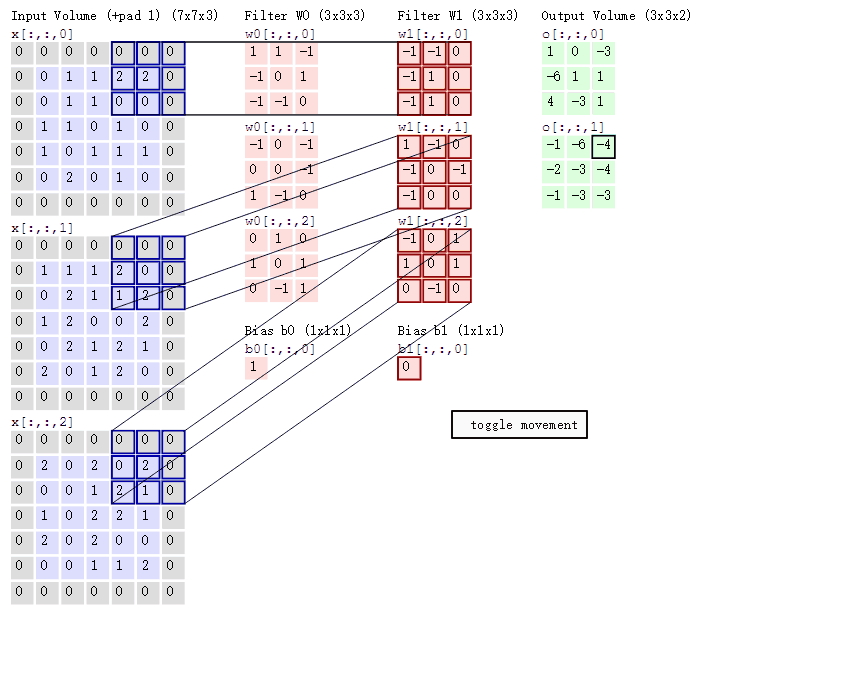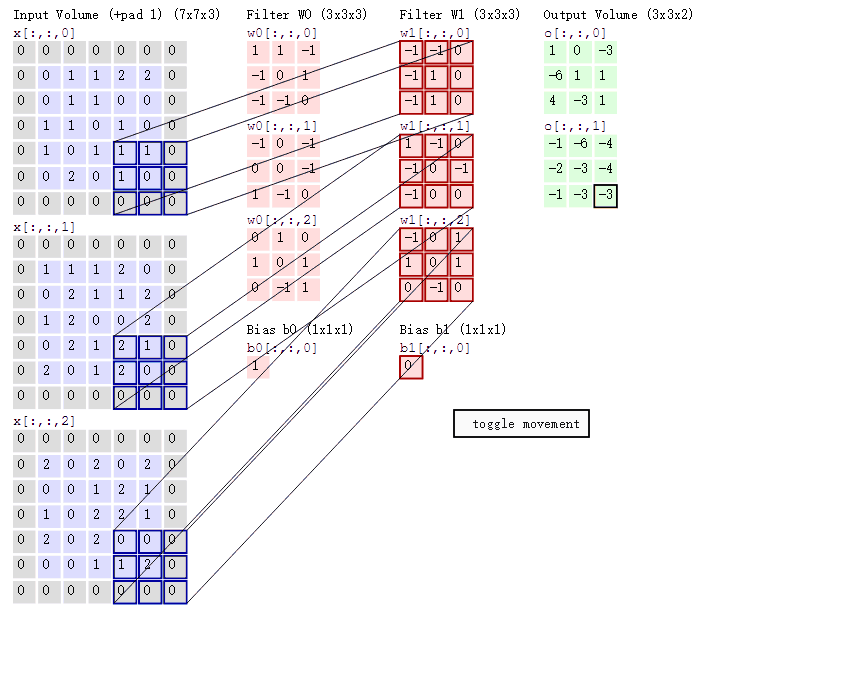
上图中,蓝色矩阵表示上一层的输出。红色矩阵表示节点的图像核,再次声明,图像核是通过训练得到的。图中,每一列即为一个节点(神经元),共2个节点。该图中,图像核的尺寸为2X2,滑动的步长为2,节点的三个参数在对应的矩阵中滑动卷积,并将卷积结果累加后与偏移项相加,输出成一个新的矩阵。
另外,卷积层也可以有激活函数,该激活函数对输出矩阵的每一个元素做运算,组合成一个新的输出矩阵后输出。常见的激活函数有Sigmoid、Relu、tanh和linear等,这里就不再介绍了。
可见,在卷积层中,节点的参数(图像核)个数等于输入矩阵的个数,输出矩阵的个数等于节点的数量。因此,我们也称节点的数量为该成的深度。若节点数为N,则图像(三通道)经过卷积层后变为N通道。
池化层
池化层可以看成只有一个节点,因此输入多少个矩阵,就输出多少个矩阵。池化层相当于cv库中的resize函数,它主要是对矩阵进行缩放,从而减少计算量,提取主要特征。
池化层缩放图像一般是根据近邻像素的平均值和最大值来缩放的。缩放图像的原理如下:
设目标图像的尺寸为Tx,Ty,源图像的尺寸为Sx,Sy。设目标图像的像素点的位置为(x',y'),则其在源图像中对应的位置(x,y)为:
故目标像素(x',y')的像素值可根据(x,y)的几个近邻的像素点,取最大值或平均值得出。如下图所示,将4X4的矩阵按最大值缩放到2X2:
综上,池化层的作用就是将每一个输入矩阵,通过上述方法缩放,从而输出缩放后的、同等数量的矩阵,作为下一层的输入。
一般而言,池化层通常“夹在”连续的卷积层中间,用于压缩特征,减少计算量。
Flatten层
Flatten层与池化层一样,可以视为带有一个节点的层。该节点将所有的输入矩阵转换为一个向量。这相当于Python中的 .flatten()函数。
例如,对于一副图像,可以用Python将其转换成向量,代码如下:
img_fea = img_rs.flatten() #图像转特征效果如下,将图像 img_rs 转换为一个向量:
Flatten层就是这样,将所有的矩阵用上述的方法转换成多个向量,然后再拼(concat)成一个总向量,作为下一层的输入。
CNN的总体结构
CNN的输入层一般为三个节点,输出RGB图像对应的三个通道(矩阵)
一般在Flatten层之前,CNN围绕着卷积层展开,连续的卷积层之间夹这用于特征压缩的池化层。在Flatten之后,一般后面接着一个BP神经网络。
在CNN中,一般节点的个数、网络的层数、用什么层(卷积、池化、Flatten、BP中普通的隐藏层等)都需要人工确定。对于卷积层,节点的参数个数(图像核个数)等于输入矩阵的数量,输出矩阵的个数等于节点的个数。对输入矩阵进行跟踪,其“加工”过程如下:
上述网络中,输入层输出一个矩阵,该矩阵通过卷积层输出多个矩阵;然后经过池化层缩放(数量不变),再经过卷积层输出多个矩阵(可以看出,该层的节点比前面的卷积层要多),再池化缩放矩阵,最后通过Flatten层将矩阵转换为向量,拼接成一个总向量;在Flatten层之后,就是BP神经网络了,BP神经网络的原理这里就不介绍了。
网络的构造
给定数据集,我们可以通过自变量x,与因变量y的数量确定输入层、输出层节点的个数。但是中间层(包括卷积层、隐藏层)的节点数是需要确定的,如何确定呢?一般视模型的实际效果而定,我们可用交叉验证的方法选择合适的节点个数。
有时候,我们也可以根据经验公式确定节点的个数。已知某一层节点的个数为n,则下一层节点的个数n',则n'的取值为:
一般选择Gorman法则选择中间层的节点数。
网络的训练与Dropout正则化
与BP神经网络一样,训练模型参数时,节点的误差由前往后传递,并根据误差调整网络的参数。
对于回归问题,可将代价函数(或风险函数、损失函数等)设置成均方误差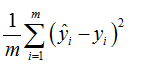
对于分类问题,可以设为0-1损失(二分类问题)
网络的训练算法可以使用Adam、RMSprop。
顺带一提,中国大学生研究出来新算法:RAdam,收敛速率高、运算速度快,一度登上GitHub的趋势版,大家可以登录到GitHub把源代码Fork下来。
另外,为了防止过拟合,通常在训练过程中,需要对模型进行正则化。比如线性回归中的Ridge、Lasso正则化,CNN也不例外。CNN的Dropout正则化是指,在训练时,依概率忽略节点。即将某些节点dropout掉,当然在使用模型时就不可以这么做。
怎么个忽略法呢?类似于将dropout的节点暂时删除。在计算训练集的预测值yi(i为样本个体i),依概率删除掉某些节点,使得这些节点不参加yi的计算工作,并且在根据代价函数调整参数时,也忽略掉这些节点的参数调节。
由于节点的颗粒度太大,忽略某个节点,则所有连接的边都会被忽略。因此除了dropout节点外,还可以dropout“神经”: