数据结构(python)

一、数据结构

student_list = [
    {'name': 'zs', 'age': 12},
    {'name': 'ls', 'age': 23}
]
student_dic = {
    {'zs'}:{'sx',23},
    {'ls'}:{'ls',24}
}

数据结构也就是存储数据的结构，我们对数据组织的方式就叫做数据结构。

比如上面保存学生信息的方式,是以列表的方式组织还是使用字典的方式组织。

数据结构解决的就是一组数据如何保存，保存形式是怎么样的。

二、线性表之顺序表

在程序中，经常需要将一组（通常是同为某个类型的）数据元素作为整体管理和使用，需要创建这种元素组，用变量记录它们，传进传出函数等。一组数据中包含的元素个数可能发生变化（可以增加或删除元素）。

对于这种需求，最简单的解决方案便是将这样一组元素看成一个序列，用元素在序列里的位置和顺序，表示实际应用中的某种有意义的信息，或者表示数据之间的某种关系。

这样的一组序列元素的组织形式，我们可以将其抽象为线性表。一个线性表是某类元素的一个集合，还记录着元素之间的一种顺序关系。线性表是最基本的数据结构之一，在实际程序中应用非常广泛，它还经常被用作更复杂的数据结构的实现基础。

根据线性表的实际存储方式，分为两种实现模型：

(1).顺序表，将元素顺序地存放在一块连续的存储区里，元素间的顺序关系由它们的存            储顺序自然表示。

(2).链表，将元素存放在通过链接构造起来的一系列存储块中。

再讲线性表之前，我们先回顾一下数据在内存中保存的形式。

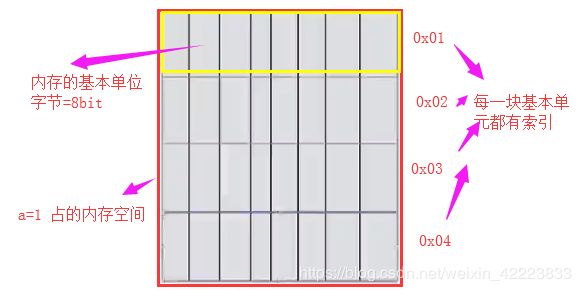
计算机的内存是真正存放数据的并且和CPU直接打交道的，我们看一下内存到底是一个怎么的模型呢。内存的基本单位是以一个字节大小，一个字节=8位

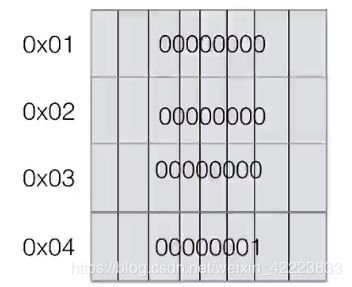
举个例子a=1 我们之前一直说在再内存中开辟了一块空间来保存1 这块空间到底是什么结构呢？

一般的整型 占28个字节，因为在python中一切皆对象，内存中除了保存数据还要保存一些其他内容。28个字节也就是28*8=224位。为了好画图我们就用4个字节来代替。

1、顺序表

将元素顺序地存放在一块连续的存储区里，元素间的顺序关系由它们的存储顺序自然表示。

例如python中的列表就是一个顺序表。

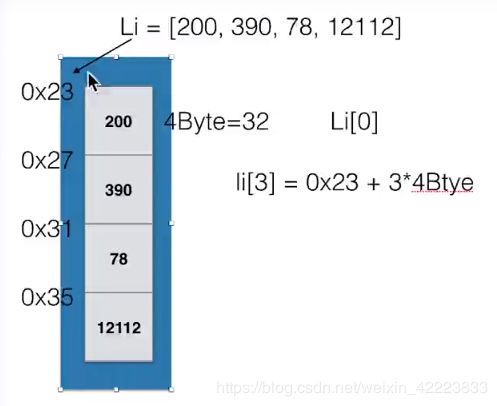
例如Li=[200,390,78,12112] 列表对应的内存图，每个元素都是连续保存的。并且我们可以通过索引偏移找到指定的元素。

我们看一下Li=[200,390,78,12112]列表在内存中的存储和怎样查找。

Li 变量实际上执行的是内存空间的第一个元素的地址，如果想查找Li[3]的值

CPU实际上是 Li[3]=0x23+3*4byte，向下偏了了3个位置。

图a表示的是顺序表的基本形式，数据元素本身连续存储，每个元素所占的存储单元大小固定相同，元素的下标是其逻辑地址，而元素存储的物理地址（实际内存地址）可以通过存储区的起始地址Loc (e0)加上逻辑地址（第i个元素）与存储单元大小（c）的乘积计算而得，即：

Loc(ei) = Loc(e0) + c*i

故，访问指定元素时无需从头遍历，通过计算便可获得对应地址。

如果元素的大小不统一，则须采用图b的元素外置的形式，将实际数据元素另行存储，而顺序表中各单元位置保存对应元素的地址信息（即链接）。由于每个链接所需的存储量相同，通过上述公式，可以计算出元素链接的存储位置，而后顺着链接找到实际存储的数据元素。注意，图b中的c不再是数据元素的大小，而是存储一个链接地址所需的存储量，这个量通常很小。

图b这样的顺序表也被称为对实际数据的索引,这是最简单的索引结构。

Li=[12,’a’,False] Int 类型占 28个字节,bool 类型 True 占28个,False 占24个字节。字符串’a’占50个字节。因此每一个数据类型开辟的空间就不同了，内存地址也就不连续了，就不能使用上面那种方式保存数据了，因此使用元素外置的顺序表进行保存数据。因为每一个元素的内存地址占用的内存空间都是相同的，因此可以保存每一个元素的内存地址

2、顺序表的结构和实现

在Python中已经对顺序表做了封装，我们就不考虑python语言到底怎样去实现的了。

我们来研究一下如果真正实现顺序表这种数据结构，我们怎样来构造自己的数据类型。

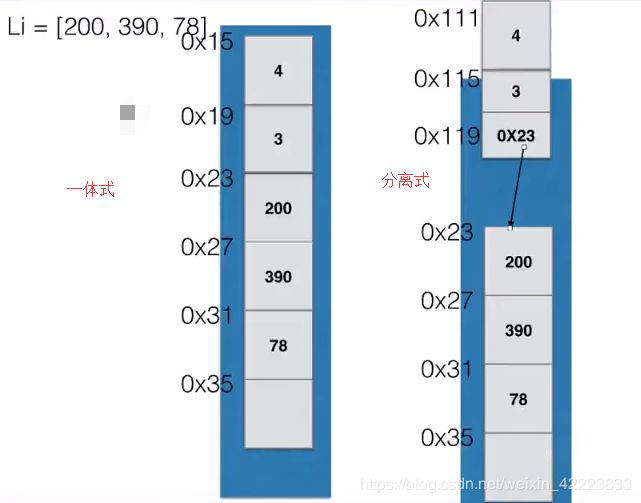
a.顺序表的两种实现方式

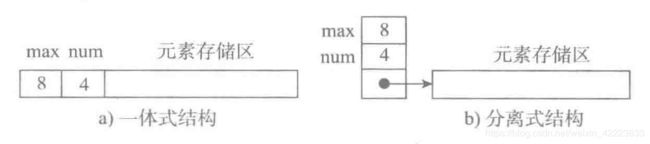
图a为一体式结构，存储表信息的单元与元素存储区以连续的方式安排在一块存储区里，两部分数据的整体形成一个完整的顺序表对象。

一体式结构整体性强，易于管理。但是由于数据元素存储区域是表对象的一部分，顺序表创建后，元素存储区就固定了。

图b为分离式结构，表对象里只保存与整个表有关的信息（即容量和元素个数），实际数据元素存放在另一个独立的元素存储区里，通过链接与基本表对象关联。

b.元素存储区替换

一体式结构由于顺序表信息区与数据区连续存储在一起，所以若想更换数据区，则只能整体搬迁，即整个顺序表对象（指存储顺序表的结构信息的区域）改变了。(例如想往Li中再添加一个元素，需要从新开辟一块空间将之前的信息保存进去还有现在刚添加的元素)

分离式结构若想更换数据区，只需将表信息区中的数据区链接地址更新即可，而该顺序表对象不变。

因此我们推荐使用分离式结构实现顺序表。

c.元素存储区扩充

采用分离式结构的顺序表，若将数据区更换为存储空间更大的区域，则可以在不改变表对象的前提下对其数据存储区进行了扩充，所有使用这个表的地方都不必修改。只要程序的运行环境（计算机系统）还有空闲存储，这种表结构就不会因为满了而导致操作无法进行。

人们把采用这种技术实现的顺序表称为动态顺序表，因为其容量可以在使用中动态变化。

扩充的两种策略

• 每次扩充增加固定数目的存储位置，如每次扩充增加10个元素位置，这种策略可称为线性增长。

特点：节省空间，但是扩充操作频繁，操作次数多。

• 每次扩充容量加倍，如每次扩充增加一倍存储空间。

特点：减少了扩充操作的执行次数，但可能会浪费空间资源。以空间换时间，推荐的方式。

总结：第一种策略是增加几个元素就扩充几个内存空间，这样节约空间但是扩充操作频繁，操作次数多。

第二种策略是，翻倍增加，减少了扩充操作的执行次数，但可能会浪费空间资源。以空间换时间，推荐的方式。

3、顺序表的操作

python中的list 列表就是一个顺序表，如果想往列表中添加数据，我们可以使用append()方法和insert(index,obj)方法来添加元素。因此我们研究一下内存中数据到底怎么变化。

(1)增加元素

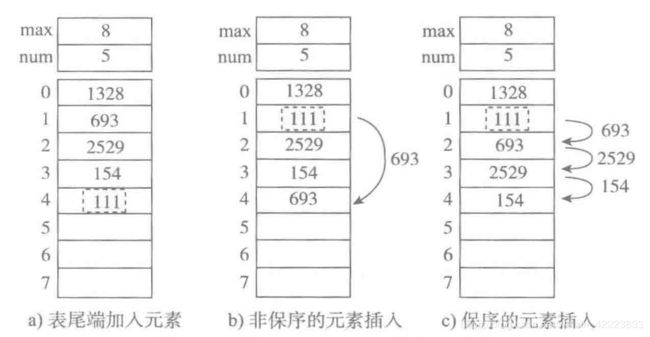
如图所示，为顺序表增加新元素111的三种方式

a. 尾端加入元素。

b. 非保序的加入元素（不常见）将原来693元素移动到最后，让将111元素

插入到指定位置，如果使用这种方式元素的位置就乱了，因此是非保存的。

c. 保序的元素加入，将693元素和后面的元素一次往下移动。但是元素之间的顺序不变，因此叫做保序。

(2).删除元素

a. 删除表尾元素，直接从尾部删除。

b. 非保序的元素删除（不常见），例如删除第一154，后面的154上移动。

c. 保序的元素删除，例如删除693，后面的元素需要依次往上移动。 

4、python中的顺序表

Python中的list和tuple两种类型采用了顺序表的实现技术，具有前面讨论的顺序表的所有性质。

tuple是不可变类型，即不变的顺序表，因此不支持改变其内部状态的任何操作，而其他方面，则与list的性质类似。

(1)、list的基本实现技术

Python标准类型list就是一种元素个数可变的线性表，可以加入和删除元素，并在各种操作中维持已有元素的顺序（即保序），而且还具有以下行为特征：

• 基于下标（位置）的高效元素访问和更新，为满足该特征，应该采用顺序表技术，表中元素保存在一块连续的存储区中。
• 允许任意加入元素，而且在不断加入元素的过程中，表对象的标识（函数id得到的值）不变(采用分离式方式)。

为满足该特征，就必须能更换元素存储区，并且为保证更换存储区时list对象的标识id不变，只能采用分离式实现技术。

在Python的官方实现中，list就是一种采用分离式技术实现的动态顺序表。

在Python的官方实现中，list实现采用了如下的策略：在建立空表（或者很小的表）时，系统分配一块能容纳8个元素的存储区；在执行插入操作（insert或append）时，如果元素存储区满就换一块4倍大的存储区。但如果此时的表已经很大（目前的阀值为50000也就是50000个元素），则改变策略，采用加一倍的方法。引入这种改变策略的方式，是为了避免出现过多空闲的存储位置。

三、线性表之链表

为什么需要链表

顺序表的构建需要预先知道数据大小来申请连续的存储空间，而在进行扩充时又需要进行数据的搬迁，所以使用起来并不是很灵活。

链表结构可以充分利用计算机内存空间（可以不用连续的开辟内存来保存数据），实现灵活的内存动态管理。

1、链表的定义

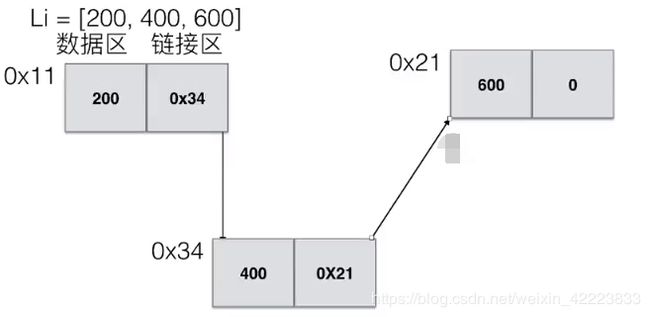
链表（Linked list）是一种常见的基础数据结构，是一种线性表，但是不像顺序表一样连续存储数据，而是在每一个节点（数据存储单元）里存放下一个节点的位置信息（即地址）。

每个节点中不仅仅保存数据，还要保存下一个节点的地址。这样通过地址将每一个元素就链接起来了。这就是链表。

链表分单向链表，双向链表。

Lst=[2,3,4,5]

2、单向链表的结构和实现

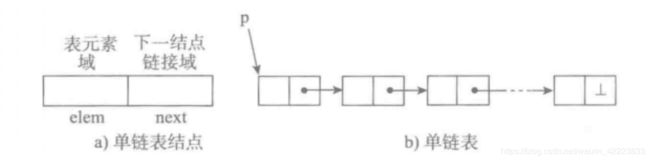
单向链表也叫单链表指的是图中的线只有一个方向，是链表中最简单的一种形式，它的每个节点包含两个域，一个信息域（元素域）和一个链接域。这个链接指向链表中的下一个节点，而最后一个节点的链接域则指向一个空值。

 

• 表元素域elem用来存放具体的数据。
• 链接域next用来存放下一个节点的位置（python中的标识）
• 变量p指向链表的头节点（首节点）的位置，从p出发能找到表中的任意节点。

(1)节点实现

class SingleNode(object):
    """单链表的结点"""
    def __init__(self, item):
        #  _item存放数据元素
        self.item = item
        #  _next是下一个节点的标识
        self.next = None

(2)单链表的操作

is_empty() 链表是否为空

length() 链表长度

travel() 遍历整个链表

add(item) 链表头部添加元素

append(item) 链表尾部添加元素

insert(pos, item) 指定位置添加元素

remove(item) 删除节点

search(item) 查找节点是否存在

(3)单链表的实现

class SingleLinkList(object):
    """单链表"""
    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head is None

    def length(self):
        """链表长度"""
        # cur初始时指向头节点
        cur = self._head
        count = 0
        # 尾节点指向None，当未到达尾部时
        while cur is not None:
            count += 1
            # 将cur后移一个节点
            cur = cur.next
        return count

    def travel(self):
        """遍历链表"""
        cur = self._head
        while cur is not None:
            print(cur.item, end=" ")
            cur = cur.next
        print()

Cur变量表示节点，如果cur 移动到了300后面的节点了，但是没有了因此是None。因此使用cur!=None 来做循环体的判断条件。

计算链表的长度，我们可以参考每一个node的链接区，如果有地址表示还存在下一个node。因为最后一个node的的链接区是None，因此可以通过判断是不是None来判断是否到了末尾。

头部添加元素

 

def add(self, item):
    """头部添加元素"""
    # 先创建一个保存item节点的值
    node = SingleNode(item)
    # 将新节点的链接域next指向头节点，即_head指向的位置
    node.next = self._head
    # 将链表的头_head指向新节点
    self._head = node

尾部添加元素

 def append(self, item):
    """尾部添加元素"""
    node = SingleNode(item)
    # 先判断链表是否为空，若是空链表，则将_head指向新节点
    if self.is_empty():
        self._head = node
    # 若不为空，则找到尾部，将尾节点的next指向新节点
    else:
        cur = self._head
        while cur.next is not None:
            cur = cur.next
        cur.next = node

指定位置添加元素

 

def insert(self, index, item):
    """指定位置添加元素"""
    # 若指定位置pos为第一个元素之前，则执行头部插入
    if index <= 0:
        self.add(item)
    # 若指定位置超过链表尾部，则执行尾部插入
    elif index > (self.length() - 1):
        self.append(item)
    # 找到指定位置
    else:
        node = SingleNode(item)
        count = 0
        # pre用来指向指定位置pos的前一个位置pos-1，初始从头节点开始移动到指定位置
        pre = self._head
        while count < (index - 1):
            count += 1
            pre = pre.next
        # 先将新节点node的next指向插入位置的节点
        node.next = pre.next
        # 将插入位置的前一个节点的next指向新节点
        pre.next = node

 删除节点

def remove(self, item):
    """删除节点"""
    cur = self._head
    pre = None
    while cur is not None:
        # 找到了指定元素
        if cur.item == item:
            # 如果第一个就是删除的节点
            if not pre:
                # 将头指针指向头节点的后一个节点
                self._head = cur.next
            else:
                # 将删除位置前一个节点的next指向删除位置的后一个节点
                pre.next = cur.next
            break
        else:
            # 继续按链表后移节点
            pre = cur
            cur = cur.next

查找节点是否存在

	 def search(self, item):
    """链表查找节点是否存在，并返回True或者False"""
    cur = self._head
    while cur is not None:
        if cur.item == item:
            return True
        cur = cur.next
    return False

3、双向链表

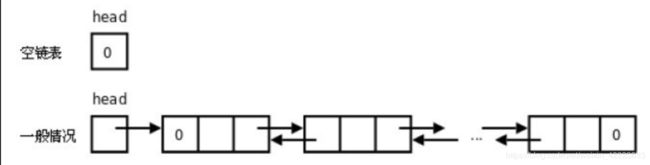
一种更复杂的链表是“双向链表”或“双面链表”。每个节点有两个链接：一个指向前一个节点，当此节点为第一个节点时，指向空值；而另一个指向下一个节点，当此节点为最后一个节点时，指向空值。

 

(1)双向链表的操作

is_empty() 链表是否为空

length() 链表长度

travel() 遍历链表

add(item) 链表头部添加

append(item) 链表尾部添加

insert(pos, item) 指定位置添加

remove(item) 删除节点

search(item) 查找节点是否存在

(2)双向链表的实现

class Node(object):
    """双向链表节点"""

    def __init__(self, item):
        self.item = item
        self.next = None
        self.prev = None

class DLinkList(object):
    """双向链表"""

    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head == None

    def length(self):
        """返回链表的长度"""
        cur = self._head
        count = 0
        while cur is not None:
            count += 1
            cur = cur.next
        return count

    def travel(self):
        """遍历链表"""
        cur = self._head
        while cur is not None:
            print(cur.item, end=" ")
            cur = cur.next
        print("")

    def add(self, item):
        """头部插入元素"""
        node = Node(item)
        if self.is_empty():
            # 如果是空链表，将_head指向node
            self._head = node
        else:
            # 将node的next指向_head的头节点
            node.next = self._head
            # 将_head的头节点的prev指向node
            self._head.prev = node
            # 将_head 指向node
            self._head = node

    def append(self, item):
        """尾部插入元素"""
        node = Node(item)
        if self.is_empty():
            # 如果是空链表，将_head指向node
            self._head = node
        else:
            # 移动到链表尾部
            cur = self._head
            while cur.next is not None:
                cur = cur.next
            # 将尾节点cur的next指向node
            cur.next = node
            # 将node的prev指向cur
            node.prev = cur

    def search(self, item):
        """查找元素是否存在"""
        cur = self._head
        while cur is not None:
            if cur.item == item:
                return True
            cur = cur.next
        return False

Add()添加操作：

 

append() 操作:

Insert()操作

 

注意: cur.prev 指的是前驱节点对象

 

remove()删除操作

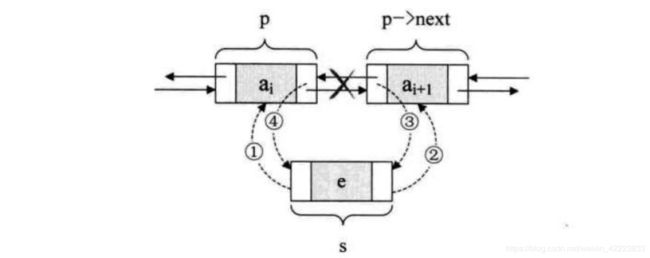
指定位置插入节点

 

def insert(self, pos, item):
    """在指定位置添加节点"""
    if pos <= 0:
        self.add(item)
    elif pos > (self.length() - 1):
        self.append(item)
    else:
        node = Node(item)
        cur = self._head
        count = 0
        # 移动到指定位置的前一个位置
        while count < (pos - 1):
            count += 1
            cur = cur.next
        # 将node的prev指向cur
        node.prev = cur
        # 将node的next指向cur的下一个节点
        node.next = cur.next
        # 将cur的下一个节点的prev指向node
        cur.next.prev = node
        # 将cur的next指向node
        cur.next = node

 

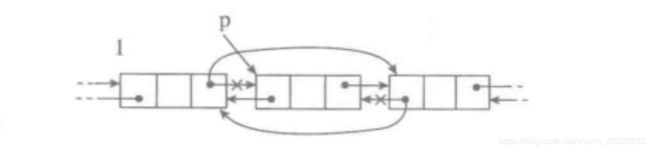
删除元素

def remove(self, item):
    """删除元素"""
    if self.is_empty():
        return
    else:
        cur = self._head
        if cur.item == item:
            # 如果首节点的元素即是要删除的元素
            if cur.next == None:
                # 如果链表只有这一个节点
                self._head = None
            else:
                # 将第二个节点的prev设置为None
                cur.next.prev = None
                # 将_head指向第二个节点
                self._head = cur.next
            return
        while cur != None:
            if cur.item == item:
                # 将cur的前一个节点的next指向cur的后一个节点
                cur.prev.next = cur.next
                # 将cur的后一个节点的prev指向cur的前一个节点
                cur.next.prev = cur.prev
                break
            cur = cur.next

四、栈

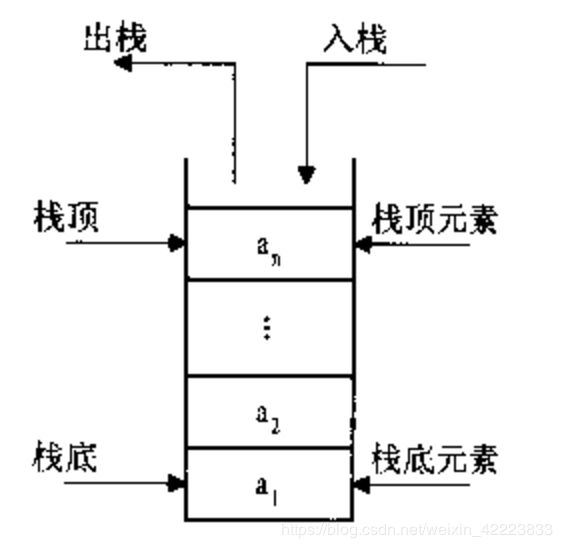
栈（stack），有些地方称为堆栈，是一种容器，可存入数据元素、访问元素、删除元素，它的特点在于只能允许在容器的一端（称为栈顶端指标，英语：top）进行加入数据（英语：push）和输出数据（英语：pop）的运算。没有了位置概念，保证任何时候可以访问、删除的元素都是此前最后存入的那个元素，确定了一种默认的访问顺序。

由于栈数据结构只允许在一端进行操作，因而按照后进先出（LIFO, Last In First Out）的原理运作。

注意：栈和队列研究的是操作层面，顺序表和链表研究的是数据怎么存放。

我们将顺序表和链表进行修改后就可以看成了栈和队列。

(1)栈的操作

• Stack() 创建一个新的空栈
• push(item) 添加一个新的元素item到栈顶
• pop() 弹出栈顶元素
• peek() 返回栈顶元素
• is_empty() 判断栈是否为空
• size() 返回栈的元素个数

(2)栈结构的实现

栈可以用顺序表实现，也可以用链表实现。

class Stack(object):
    """栈"""
    def __init__(self):
        self.items = []

    def is_empty(self):
        """判断是否为空"""
        return self.items == []

    def push(self, item):
        """加入元素"""
        self.items.append(item)

    def pop(self):
        """弹出元素"""
        return self.items.pop()

    def peek(self):
        """返回栈顶元素"""
        return self.items[len(self.items) - 1]

    def size(self):
        """返回栈的大小"""
        return len(self.items)

if __name__ == "__main__":
    stack = Stack()
    stack.push("hello")
    stack.push("world")
    stack.push("itcast")
    print(stack.size())
    print(stack.peek())
    print(stack.pop())
    print(stack.pop())
    print(stack.pop())
    print(stack.size())

五、队列

队列（queue）是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。

队列是一种先进先出的（First In First Out）的线性表，简称FIFO。允许插入的一端为队尾，允许删除的一端为队头。队列不允许在中间部位进行操作！假设队列是q=（a1，a2，……，an），那么a1就是队头元素，而an是队尾元素。这样我们就可以删除时，总是从a1开始，而插入时，总是在队列最后。这也比较符合我们通常生活中的习惯，排在第一个的优先出列，最后来的当然排在队伍最后。

(1)队列的操作

• Queue() 创建一个空的队列
• enqueue(item) 往队列中添加一个item元素
• dequeue() 从队列头部删除一个元素
• is_empty() 判断一个队列是否为空
• size() 返回队列的大小

(2)队列的实现

队列可以用顺序表实现。

class Queue(object):
    """队列"""
    def __init__(self):
        self.items = []

    def is_empty(self):
        return self.items == []

    def enqueue(self, item):
        """进队列"""
        self.items.insert(0, item)

    def dequeue(self):
        """出队列"""
        return self.items.pop()

    def size(self):
        """返回大小"""
        return len(self.items)

if __name__ == "__main__":
    q = Queue()
    q.enqueue("hello")
    q.enqueue("world")
    q.enqueue("itcast")
    print(q.size())
    print(q.dequeue())
    print(q.dequeue())
    print(q.dequeue())

(3)双端队列

双端队列（deque，全名double-ended queue），是一种具有队列和栈的性质的数据结构。

双端队列中的元素可以从两端弹出，其限定插入和删除操作在表的两端进行。双端队列可以在队列任意一端入队和出队。

1、 双端队列的操作

1. Deque() 创建一个空的双端队列
2. add_front(item) 从队头加入一个item元素
3. add_rear(item) 从队尾加入一个item元素
4. remove_front() 从队头删除一个item元素
5. remove_rear() 从队尾删除一个item元素
6. is_empty() 判断双端队列是否为空
7. size() 返回队列的大小

2、双端队列的实现

class Deque(object):
    """双端队列"""

    def __init__(self):
        self.items = []

    def is_empty(self):
        """判断队列是否为空"""
        return self.items == []

    def add_front(self, item):
        """在队头添加元素"""
        self.items.insert(0, item)

    def add_rear(self, item):
        """在队尾添加元素"""
        self.items.append(item)

    def remove_front(self):
        """从队头删除元素"""
        return self.items.pop(0)

    def remove_rear(self):
        """从队尾删除元素"""
        return self.items.pop()

    def size(self):
        """返回队列大小"""
        return len(self.items)

if __name__ == "__main__":
    deque = Deque()
    deque.add_front(1)
    deque.add_front(2)
    deque.add_rear(3)
    deque.add_rear(4)
    print(deque.size())
    print(deque.remove_front())
    print(deque.remove_front())
    print(deque.remove_rear())
    print(deque.remove_rear())