街景字符编码识别项目学习笔记（五）模型训练与验证

内容简介

学习笔记（四）中，初步介绍了以AlexNet为实例用pytorch实现卷积神经网络的方式，并对赛题所应用的baseline定长字符识别模型进行了建立。本节中，我们主要关注模型建立之后的训练以及验证过程。

模型训练与验证

神经网络的训练过程实际上就是网络对输入数据进行特征提取的过程。通过模型预测输出和给定输出之间误差的损失函数的梯度反作用于网络，以更新网络当中的参数值，从而提高模型对给定任务的解决能力。

可以想象，在实际训练过程当中，模型会倾向于增强对输入数据的特征提取能力，因为同样的数据往往会输入到网络很多次以达到训练的效果，这样的数据也被称之为训练数据、训练集。不过我们理想当中的网络模型，不仅仅能够对这样反复输入的数据有足够强的表示能力，还需要对其他同类型的数据有着同样的表示能力，更准确地说，是对理想中同分布的数据有着同等能力地表示。

因此，我们需要从原始的数据集当中划分出来一批，来进行对网络泛化能力的测试，称之为测试集。训练集上的误差被称之为训练误差，测试集上的误差被称之为测试误差（泛化误差）。实际网络训练的训练误差与测试误差（泛化误差）之间的关系大概如下图所示：

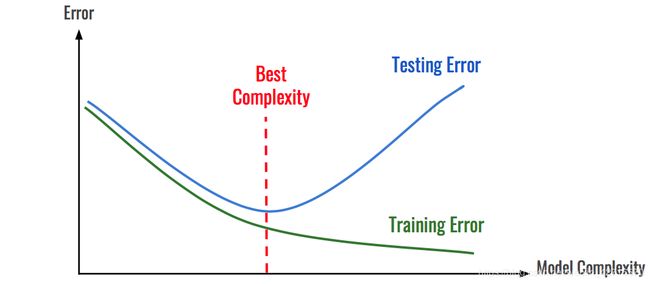
随着模型复杂度的上升，我们可以得到一个对训练集数据表征更强的模型，但是这样的模型的测试误差会逐渐增加，这违背了我们的初衷，这样的问题也被称之为过拟合。

在工程实践当中，我们需要利用各种各样的技巧来减少过拟合的现象。以下介绍在不改变模型的基础上如何尽可能得减小模型的过拟合程度。

模型训练方法技巧总结

留出法（Hold-Out）
直接将训练集划分成两部分，新的训练集和验证集。这种划分方式的优点是最为直接简单；缺点是只得到了一份验证集，有可能导致模型在验证集上过拟合。留出法应用场景是数据量比较大的情况。

交叉验证法（Cross Validation，CV）
将训练集划分成K份，将其中的K-1份作为训练集，剩余的1份作为验证集，循环K训练。这种划分方式是所有的训练集都是验证集，最终模型验证精度是K份平均得到。这种方式的优点是验证集精度比较可靠，训练K次可以得到K个有多样性差异的模型；CV验证的缺点是需要训练K次，不适合数据量很大的情况。

自助采样法（BootStrap）
通过有放回的采样方式得到新的训练集和验证集，每次的训练集和验证集都是有区别的。这种划分方式一般适用于数据量较小的情况。

这三种方法的总结如下图所示：

模型训练与验证 by pytorch

学习笔记（二）中有traning by pytorch style的部分，以及一套关于神经网络的全流程描述，在此援引神经网络训练部分以供读者理解模型训练过程的大致逻辑。
定义神经网络基本架构，其中包含两层全连接层 输入为32*32的三通道图像

模型构建与训练逻辑流程

import torch
import torch.nn
import torch.nn.functional as F #取pytorch当中已经定义好的函数

#定义神经网络的基本架构
class Net(nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        self.fc1 = nn.Linear(32*32*3,500)
        self.fc2 = nn.Linear(500,10)
        
    def forward(self,x):
        x = F.relu(self.fc1(x))
        return self.fc2(x)

net = Net() #实例化神经网络
criterion = nn.CrossEntropyLoss() #采用交叉熵函数作为输出与ground truth的衡量标准
optimizer = optim.Adam(net.parameters(),lr=3e-4) #这里定义优化器 采用Adam作为梯度下降算法 同时加上权重的二范数正则化项 正则化项的系数为lr变量

for eopch in range(10): #定义训练进行的epoch数目
    for i,data in enmerate(trainloader,0):
        inputs,label = data
        inputs = inputs.view(-1,32*32*3) #view方法是对张量的行列进行重新排列 此处转换为1行32*32*3的张量
        optimizer.zero_grad() #将梯度全部初始化为0
        outputs = net(inputs)
        loss = criterion(output,labels)
        loss.backward() #建立梯度的反向传播过程 反向传播求解梯度
        optimizer.step() #将模型当中的所有参数针对梯度进行更新

模型验证逻辑

correct.total = 0,0 #定义正确的数目和全部的数目
predictions = []
net.eval()

for i,data in enumerate(testloader,0): #获取testloader当中输入数据和对应的标签
    inputs,labels = data               #inputs为数据输入，labels为数据的标签
    outputs = net(inputs)              #获取 一系列的网络输出
    ~,predicted = torch.max(outputs.data,1)  #获取网络的预测值
    predictions.append(outputs)              #把所有预测值放入一个list当中
    total += labels.size(0)                  #确定labels的总数
    correct += (predicted == labels).sum().item()  #计算网络的正确率

print('The acc is: %d %%'%(100*correct/total))

字符识别模型的网络训练与验证过程

对本次项目当中运用的神经网络模型的训练与验证过程代码如下所示：

train_loader = torch.utils.data.DataLoader(
    train_dataset,
    batch_size=10, 
    shuffle=True, 
    num_workers=10, 
)
    
val_loader = torch.utils.data.DataLoader(
    val_dataset,
    batch_size=10, 
    shuffle=False, 
    num_workers=10, 
)

model = SVHN_Model1()
criterion = nn.CrossEntropyLoss (size_average=False)
optimizer = torch.optim.Adam(model.parameters(), 0.001)
best_loss = 1000.0
for epoch in range(20):
    print('Epoch: ', epoch)

    train(train_loader, model, criterion, optimizer, epoch)
    val_loss = validate(val_loader, model, criterion)
    
    # 记录下验证集精度
    if val_loss < best_loss:
        best_loss = val_loss
        torch.save(model.state_dict(), './model.pt')

其中每个Epoch的训练代码如下：

def train(train_loader, model, criterion, optimizer, epoch):
    # 切换模型为训练模式
    model.train()

    for i, (input, target) in enumerate(train_loader):
        c0, c1, c2, c3, c4, c5 = model(data[0])
        loss = criterion(c0, data[1][:, 0]) + \
                criterion(c1, data[1][:, 1]) + \
                criterion(c2, data[1][:, 2]) + \
                criterion(c3, data[1][:, 3]) + \
                criterion(c4, data[1][:, 4]) + \
                criterion(c5, data[1][:, 5])
        loss /= 6
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

其中每个Epoch的验证代码如下：

def validate(val_loader, model, criterion):
    # 切换模型为预测模型
    model.eval()
    val_loss = []

    # 不记录模型梯度信息
    with torch.no_grad():
        for i, (input, target) in enumerate(val_loader):
            c0, c1, c2, c3, c4, c5 = model(data[0])
            loss = criterion(c0, data[1][:, 0]) + \
                    criterion(c1, data[1][:, 1]) + \
                    criterion(c2, data[1][:, 2]) + \
                    criterion(c3, data[1][:, 3]) + \
                    criterion(c4, data[1][:, 4]) + \
                    criterion(c5, data[1][:, 5])
            loss /= 6
            val_loss.append(loss.item())
    return np.mean(val_loss)
    

模型的测试和加载

在Pytorch中模型的保存和加载非常简单，比较常见的做法是保存和加载模型参数：
torch.save(model_object.state_dict(), 'model.pt')
model.load_state_dict(torch.load(' model.pt'))

模型的调参

深度学习实践性非常强，基本上很多的模型的验证只能通过训练来完成。同时深度学习有众多的网络结构和超参数，因此需要反复尝试。训练深度学习模型需要GPU的硬件支持，也需要较多的训练时间，如何有效的训练深度学习模型逐渐成为了一门学问。调参相关流程图总结如下：