Tsp问题使用遗传算法求解以及python代码

Tsp问题

旅行商问题，即TSP问题（Traveling Salesman Problem）又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
因为Hamilton问题在tsp中相对简单，博主本意是要练习使用遗传算法，所以这里是想办法对hamilton获取相对优解。

遗传算法介绍

Tsp问题有很多种解法，但是对于这样的图论问题。学界还没有提出一种遍历之外的精确解法，因此一般使用遗传算法、禁忌搜索等容易解序列问题的智能算法来对Tsp求近似解。禁忌算法容易陷入局部最优，而且没有遗传算法灵活，因此我将使用遗传算法来求解这个问题。
遗传算法是一种受孟德尔遗传定理启发而得到的智能算法，通过把解当作基因，迭代基因获得更优的解。有一篇博客我觉得对于这个算法解释得非常详细，因此我就不对这个算法再进行缀述了。留个传送门给你们了解： https://blog.csdn.net/qq_31805821/article/details/79763326

遗传算法用在tsp的问题

由于hamilton问题中我们只能遍历一遍每个城市，但是遗传算法中的染色体互换可能会导致一条基因上有两个相同的元素。因此我们必须设计一种特殊的染色体交叉方法。
我们使用此方法解决元素重叠的问题。该方法参考了博客：https://blog.csdn.net/greedystar/article/details/80343841

代码实现

其他详细细节我就不说了，因为遗传算法总的来说还是相对容易实现的。我直接贴上python代码，如果还有不了解的看完代码之后基本也了解了。

节点生成

首先，我们要随机生成一些节点，以模拟tsp问题中的城市：

def tsp_port(port_num=50, x_range=2500, y_range=2500):
    return np.random.randint(0, x_range, port_num), np.random.randint(0, y_range, port_num)

GA

然后，我们就可以把遗传算法写出来了：

class Gant:
    def __init__(self, port_num=50, x_range=2500, y_range=2500, gants_num=1000):
        print('init...')
        self.x, self.y = tsp_port(port_num, x_range, y_range)           # 随机生成的城市坐标
        self.port_num = port_num                                        # 节点数量
        self.x_range = x_range                                          # 地图范围
        self.y_range = y_range
        self.gants_num = gants_num                                      # 种群规模
        self.gants = []
        self.get_new_gants()                                            # 随机初始化种群基因

    def get_new_gants(self):
        for i in range(self.gants_num):
            self.gants.append(np.random.permutation(self.port_num))

    def get_distance(self, i):
        distance = 0
        gant = self.gants[i]
        for j in range(1, self.port_num):
            distance += pow(self.x[gant[j]]-self.x[gant[j-1]], 2) + pow(self.y[gant[j]]-self.y[gant[j-1]], 2)
        return distance

    def get_distances(self):
        dists = []
        for i in range(self.gants_num):
            dists.append([self.get_distance(i), i])
        return sorted(dists)

    def select(self):
        res = []
        dists = self.get_distances()
        strong = int(self.gants_num/5)
        for i in range(strong):          # 取出强者部分，强者直接选择
            res.append(dists[i])
        sele = np.random.permutation(strong*4)
        for i in range(strong):          # 取出幸运群体
            res.append(dists[i+strong])
        return res

    def cover(self, population):                    # 繁殖
        new_population = []
        rand = np.random.permutation(int(self.gants_num/5))
        for i in range(int(self.gants_num/5)):
            father1 = self.gants[population[rand[i] * 2][1]]
            father2 = self.gants[population[rand[i] * 2 + 1][1]]
            cut_point_low = np.random.randint(self.port_num-1)
            cut_point_high = np.random.randint(cut_point_low, self.port_num)
            cut_gant = father1[cut_point_low:cut_point_high]
            son1 = cp.copy(father1)
            son2 = cp.copy(father2)
            father_to_son1 = []
            k = 0
            for j in range(self.port_num):

                if father2[j] not in cut_gant:
                    father_to_son1.append(father2[j])
                else:
                    son2[j] = cut_gant[k]
                    k += 1
            # print(cut_point_low, cut_point_high, np.shape(father_to_son1))
            # if self.port_num - cut_point_high + cut_point_low != np.shape(father_to_son1)[0]:
            #     print(father_to_son1, cut_gant, father1, father2, len(set(father1)))
            if cut_point_low == 0 and cut_point_high == self.port_num:
                son1 = father2
                son2 = father1
            elif cut_point_low == 0:
                son1[cut_point_high:self.port_num] = np.array(father_to_son1)
            elif cut_point_high == self.port_num:
                son1[0:cut_point_low] = np.array(father_to_son1)
            else:
                son1[0:cut_point_low] = np.array(father_to_son1[0:cut_point_low])
                son1[cut_point_high:self.port_num] = np.array(father_to_son1[cut_point_low:])
            new_population.append(father1)
            new_population.append(father2)
            new_population.append(son1)
            new_population.append(son2)
        # 变异
        rand = np.random.choice(int(self.gants_num/5)*4, int(self.gants_num/5), replace=False)
        for i in rand:
            new_gant = cp.copy(new_population[i])
            rand_mod = np.random.randint(int(self.gants_num/40))
            # if rand_mod == 0:
            for l in range(rand_mod):
                exchange = np.random.choice(self.port_num, 2)
                a = new_gant[exchange[0]]
                new_gant[exchange[0]] = new_gant[exchange[1]]
                new_gant[exchange[1]] = a
            # elif rand_mod == 1:
            #     exchangelong = np.random.randint(1, int(self.port_num/10))
            #     exchangepoint = np.random.randint(exchangelong, self.port_num - exchangelong)
            #     a = new_gant[exchangepoint: exchangepoint + exchangelong]
            #     new_gant[exchangepoint: exchangepoint + exchangelong] = \
            #         new_gant[exchangepoint - exchangelong: exchangepoint]
            #     new_gant[exchangepoint - exchangelong: exchangepoint] = a
            # else:
            #     # randint的随机范围是[x,y)
            #     exchangelong = np.random.randint(1, int(self.port_num / 10))
            #     exchangepoint1 = np.random.randint(0, self.port_num - exchangelong*2)
            #     exchangepoint2 = np.random.randint(exchangepoint1, self.port_num - exchangelong)
            #     a = new_gant[exchangepoint1: exchangepoint1 + exchangelong]
            #     new_gant[exchangepoint1: exchangepoint1 + exchangelong] = \
            #         new_gant[exchangepoint2: exchangepoint2 + exchangelong]
            #     new_gant[exchangepoint2: exchangepoint2 + exchangelong] = a
            if len(set(new_gant)) != self.port_num:
                # print(exchangelong, new_gant, rand_mod, len(set(new_gant)))
                exit()
            new_population.append(new_gant)
            # print(np.shape(new_gant), type(new_gant))
        self.gants = new_population
        # for i in range(int(self.gants_num/5)):
        #     print(np.shape(np.random.permutation(self.port_num)), type(np.random.permutation(self.port_num)))
        #     new_population.append(np.random.permutation(self.port_num))
        # self.gants = new_population

    def draw_roadline(self):
        dists = self.get_distances()
        shortest_line = dists[0][1]
        plt.scatter(self.x, self.y)

        plt.plot(self.x[self.gants[shortest_line]], self.y[self.gants[shortest_line]])
        plt.show()
        plt.ion()

    def train(self, op=1000):
        for i in range(op):
            res = self.select()
            self.cover(res)
            dist = self.get_distances()
            if i%500 == 0:
                self.draw_roadline()
            print("distance:", dist[0][0], "op:", i)
            # print(self.gants, np.shape(self.gants[0]))

    def train_op(self, i):
        res = self.select()
        self.cover(res)
        dist = self.get_distances()
        print("distance:", dist[0][0], "op:", i )

训练

这里我选择了40个城市，迭代了1000次。

gant = Gant(port_num=40)
gant.train(1000)
gant.draw_roadline()

结果

训练之前，随机生成的一条路径是这样的：

经过500次迭代之后：

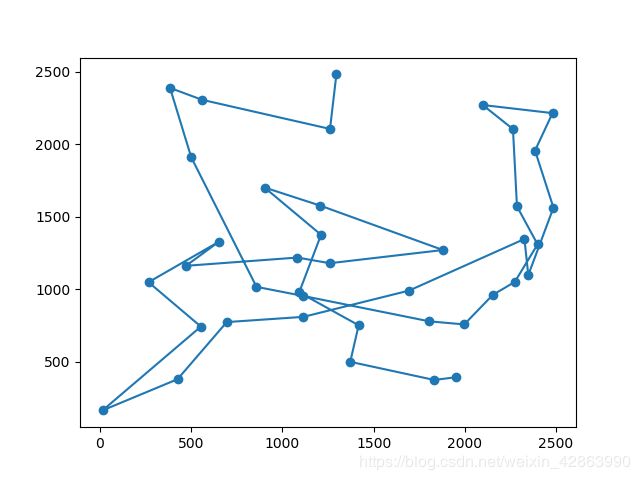
1000代之后：
可以看到由于物种的形态已经逐渐稳定下来了，大致路线与500次迭代的相差无几，只是优化了部分路线而已。。。我见到一些智能算法库中的GA能获得非常好的结果，可能是我的繁殖和变异算法写得不够好吧。。。

总结

总的来说，其实代码里面的变异部分写得不是很好，因为对于Tsp问题，有时候次优路径和最优路径的区别是非常大的，如果在种群迭代前期没办法获得比较容易混淆次优和最优的路径，可能到最后就只能很遗憾地看到次优路径而因为变异能力不足毫无办法。如果变异能力非常充足的话，变异就相当于随机生成新物种了，在多节点tsp中优化速度极慢，现在我还没有想到什么解决办法，如果有兴趣可以一起谈论呀！