1 树
1.1 完全二叉树
asdf
1.1.1 共同部分
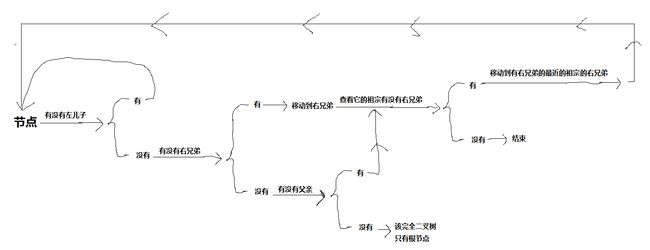
1.1.2 前序遍历
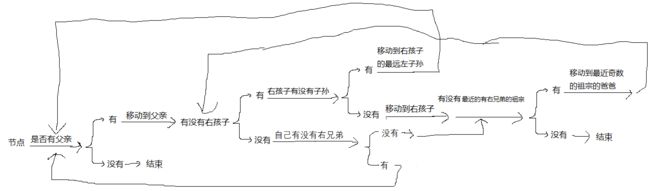
1.1.3 中序遍历
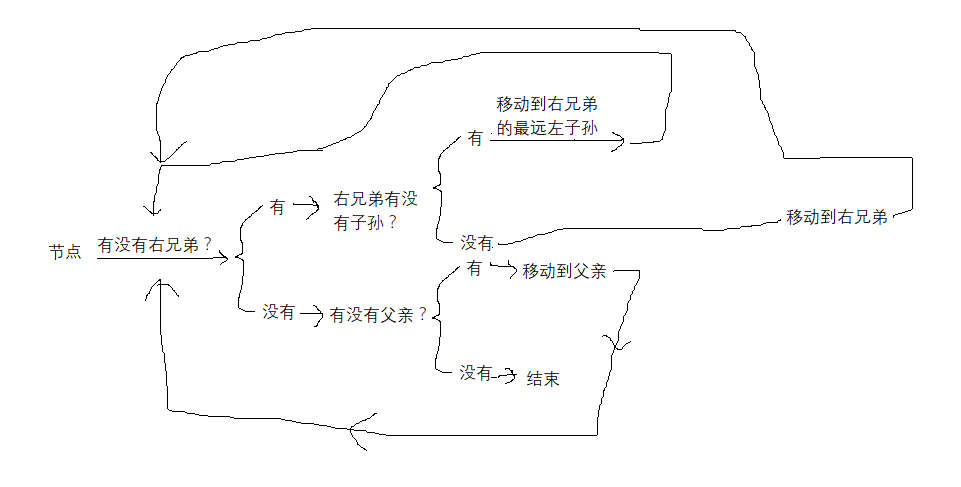
1.1.4 后序遍历
import java.util.*;
public class MyTree {
public static void main(String[] args) {
}
//已知节点总数,求树的层数
public static int 求树的层数(int 节点总数){
if(节点总数>0){
int 临时变量=2;
int 返回值=1;
while(临时变量<=节点总数){
临时变量=临时变量*2;
返回值++;
}
return 返回值;
}else{
return -1;
}
}
//已知树的层树,求树的左侧索引
public static ArrayList 求树的左侧索引(int 树的层树){
ArrayList 返回值=new ArrayList<>();
if(树的层树>0){
int 临时变量=0;
for (int i = 0; i < 树的层树; i++) {
返回值.add(临时变量);
临时变量=临时变量*2+1;
}
return 返回值;
}else{
返回值.add(-1);
return 返回值;
}
}
//求父节点索引
public static int 求父节点索引(int 自己的索引){
if(自己的索引==0){
return -1;
}
if(自己的索引>0){
return (自己的索引+1)/2-1;
}else{
return -1;
}
}
//求左儿子节点索引
public static int 求左儿子节点索引(int 自己的索引,int 节点总数){
if(自己的索引*2+1>节点总数-1){
return -1;
}else{
return 自己的索引*2+1;
}
}
//求右儿子节点索引
public static int 求右儿子节点索引(int 自己的索引,int 节点总数){
if(自己的索引*2+2>节点总数-1){
return -1;
}else{
return 自己的索引*2+2;
}
}
//返回最近的有右兄弟的祖宗
public static int 返回最近的有右兄弟的祖宗(int 自己的索引){
if(自己的索引==0){
return -1;
}
int 临时变量=自己的索引;
for(;;){
临时变量=求父节点索引(临时变量);
if(临时变量%2==1){
return 临时变量;
}else if(临时变量==0){
临时变量=-1;
return 临时变量;
}
}
}
//求最远左子孙
public static int 求最远左子孙(int 自己的索引,int 节点总数){
if(自己的索引*2+1>节点总数){
return -1;
}
int 返回值=自己的索引;
while(返回值*2+1<=节点总数-1){
返回值=返回值*2+1;
}
return 返回值;
}
//求自己的右兄弟
public static int 求自己的右兄弟(int 自己的索引,int 节点总数){
if(自己的索引%2==0){
return -1;
}
if(自己的索引+1<=节点总数-1){
return 自己的索引+1;
}else {
return -1;
}
}
//前序遍历二叉树
public static LinkedList 前序遍历二叉树(int 节点总数){
LinkedList 前序遍历索引=new LinkedList<>();
int 当前索引=0;
前序遍历索引.add(当前索引);
for(;;){
//有没有左儿子
if(求左儿子节点索引(当前索引,节点总数)>0){ //有
当前索引=求左儿子节点索引(当前索引,节点总数);
前序遍历索引.add(当前索引);
}else{ //没有
//有没有右兄弟
if(当前索引%2==1&&当前索引!=节点总数-1){ //有
//移动到右兄弟
当前索引++;
前序遍历索引.add(当前索引);
//查看它的祖宗有没有右兄弟
if(返回最近的有右兄弟的祖宗(当前索引)>0){ //有
当前索引=返回最近的有右兄弟的祖宗(当前索引)+1;
前序遍历索引.add(当前索引);
}else{ //没有
break;
}
}else{ //没有
//有没有父亲
if(当前索引==0){ //没有
break;
}else{ //有
//查看它的祖宗有没有右兄弟
if(返回最近的有右兄弟的祖宗(当前索引)>0){ //有
当前索引=返回最近的有右兄弟的祖宗(当前索引)+1;
前序遍历索引.add(当前索引);
}else{ //没有
break;
}
}
}
}
}
return 前序遍历索引;
}
//中序遍历二叉树
public static LinkedList 中序遍历二叉树(int 节点总数) {
LinkedList 中序遍历索引 = new LinkedList<>();
int 当前索引=求最远左子孙(0,节点总数);
中序遍历索引.add(当前索引);
a:for(;;){
//是否有父亲
if(求父节点索引(当前索引)>=0){ //有
当前索引=求父节点索引(当前索引);
中序遍历索引.add(当前索引);
b:for(;;){
//有没有右儿子
if(求右儿子节点索引(当前索引,节点总数)>0){ //有
int 右儿子节点=求右儿子节点索引(当前索引,节点总数);
//右孩子有没有子孙
if(求左儿子节点索引(右儿子节点,节点总数)>0){ //有
当前索引=求最远左子孙(右儿子节点,节点总数);
中序遍历索引.add(当前索引);
continue a;
}else{ //没有
当前索引=右儿子节点;
中序遍历索引.add(当前索引);
//有没有最近的有右兄弟的祖宗
if(返回最近的有右兄弟的祖宗(当前索引)==-1){ //没有
break a;
}else{ //有
当前索引=求父节点索引(返回最近的有右兄弟的祖宗(当前索引));
中序遍历索引.add(当前索引);
continue b;
}
}
}else{ //没有
//自己有没有有兄弟
if(求自己的右兄弟(当前索引,节点总数)>0){ //有
continue a;
}else{ //没有
//有没有最近的有右兄弟的祖宗
if(返回最近的有右兄弟的祖宗(当前索引)==-1){ //没有
break a;
}else{ //有
当前索引=求父节点索引(返回最近的有右兄弟的祖宗(当前索引));
中序遍历索引.add(当前索引);
continue b;
}
}
}
}
}else{ //没有
break a;
}
}
return 中序遍历索引;
}
//后序遍历二叉树
public static LinkedList 后序遍历二叉树(int 节点总数) {
LinkedList 后序遍历索引 = new LinkedList<>();
int 当前索引=求最远左子孙(0,节点总数);
后序遍历索引.add(当前索引);
for (;;){
//有没有右兄弟?
if(求自己的右兄弟(当前索引,节点总数)>0){ //有
int 自己的右兄弟=求自己的右兄弟(当前索引,节点总数);
//右兄弟有没有子孙?
if(求左儿子节点索引(自己的右兄弟,节点总数)>0){ //有
当前索引=求最远左子孙(自己的右兄弟,节点总数);
后序遍历索引.add(当前索引);
continue;
}else{ //没有
当前索引=自己的右兄弟;
后序遍历索引.add(当前索引);
continue;
}
}else{ //没有
//有没有父亲?
if(求父节点索引(当前索引)>=0){ //有
当前索引=求父节点索引(当前索引);
后序遍历索引.add(当前索引);
continue;
}else{ //没有
break;
}
}
}
return 后序遍历索引;
}
}
2 排列
2.1 二分法插入排序
3 图论
3.1 构建图
public class Graph{
public static void main(String[] args) {
Integer[] guanxi={
//0,1,2,3,4,5,6,7,8
0,1,5,0,0,0,0,0,0, //0
1,0,3,7,5,0,0,0,0, //1
5,3,0,0,1,7,0,0,0, //2
0,7,0,0,2,0,3,0,0, //3
0,5,1,2,0,3,6,9,0, //4
0,0,7,0,3,0,0,5,0, //5
0,0,0,3,6,0,0,2,7, //6
0,0,0,0,9,5,2,0,4, //7
0,0,0,0,0,0,7,4,0, //8
};
String[] hang={"0","1","2","3","4","5","6","7","8"};
String[] lie={"0","1","2","3","4","5","6","7","8"};
ArrayList 行=new ArrayList<>(Arrays.asList(hang));
ArrayList 列=new ArrayList<>(Arrays.asList(lie));
ArrayList 关系=new ArrayList<>(Arrays.asList(guanxi));
///////////////////////////////////////////////////////////////////////
HashMap>> 图=构建图2(行,列,关系,"6");
}
public static HashMap 求和某个节点连接的所有节点(ArrayList 行,ArrayList 列,
ArrayList 关系,String 节点){
int 元素个数=行.size();
HashMap 返回值=new HashMap<>();
int 关系里的起始索引=行.size()*列.indexOf(节点);
int 关系里的结束索引=行.size()*(列.indexOf(节点)+1)-1;
for (int j =关系里的起始索引; j <=关系里的结束索引 ; j++) {
if(关系.get(j)!=0){
返回值.put(行.get(j%元素个数),关系.get(j));
}
}
return 返回值;
}
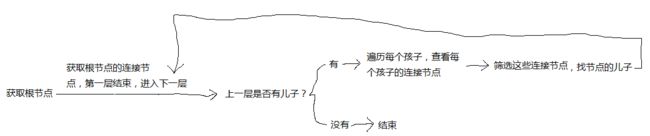
public static HashMap>> 构建图2(ArrayList 行,ArrayList 列,
ArrayList 关系,String 顶点){
HashMap>> 返回值=new HashMap<>();
int 元素个数=行.size();
//获取根节点的连接节点
int 当前层数=1;
if(当前层数==1){
ArrayList> 每层集合=new ArrayList<>();
ArrayList 根节点的连接节点=new ArrayList<>();
HashMap 每层的每个元素=new HashMap<>();
每层的每个元素.put("元素", 顶点);
int 关系里的起始索引=行.size()*列.indexOf(顶点);
int 关系里的结束索引=行.size()*(列.indexOf(顶点)+1)-1;
for (int j =关系里的起始索引; j <=关系里的结束索引 ; j++) {
if(关系.get(j)!=0){
根节点的连接节点.add(行.get(j%元素个数));
}
}
每层的每个元素.put("儿子",根节点的连接节点);
每层集合.add(每层的每个元素);
返回值.put(当前层数,每层集合 );
}
//第一层结束,进入下一层
当前层数++;
for(;;){
//上一层是否有儿子?
HashMap> 上一层的儿子集合=new HashMap<>();
for (HashMap 每层的每个元素 : 返回值.get(当前层数-1)) {
for (String 每个儿子 : (ArrayList)每层的每个元素.get("儿子")) {
//上一层的儿子集合里有没有每个儿子?
if(上一层的儿子集合.get(每个儿子)==null){ //没有
ArrayList 临时数组=new ArrayList<>();
临时数组.add((String)每层的每个元素.get("元素"));
上一层的儿子集合.put(每个儿子,临时数组);
}else{ //有
上一层的儿子集合.get(每个儿子).add((String)每层的每个元素.get("元素"));
}
}
}
if(上一层的儿子集合.size()==0){ //上一层没有儿子
break;
}else{ //上一层有儿子
Set 上一层的儿子集合所有键=上一层的儿子集合.keySet();
ArrayList> 每层集合=new ArrayList<>();
for (String 上一层的每个儿子 : 上一层的儿子集合所有键) {
HashMap 每层的每个元素=new HashMap<>();
ArrayList 兄弟=new ArrayList<>();
ArrayList 儿子=new ArrayList<>();
每层的每个元素.put("元素",上一层的每个儿子);
每层的每个元素.put("父亲",上一层的儿子集合.get(上一层的每个儿子));
int 关系里的起始索引=元素个数*列.indexOf(上一层的每个儿子);
int 关系里的结束索引=元素个数*(列.indexOf(上一层的每个儿子)+1)-1;
for (int j =关系里的起始索引; j <=关系里的结束索引 ; j++) {
if(关系.get(j)!=0){
//System.out.println(行.get(j%元素个数));
if(上一层的儿子集合.get(上一层的每个儿子).contains(行.get(j%元素个数))){ //是父亲
}else if(上一层的儿子集合所有键.contains(行.get(j%元素个数))){ //是兄弟
兄弟.add(行.get(j%元素个数));
}else{ //是儿子
儿子.add(行.get(j%元素个数));
}
}
}
每层的每个元素.put("本层所有元素",上一层的儿子集合所有键);
每层的每个元素.put("儿子",儿子);
每层的每个元素.put("兄弟",兄弟);
每层集合.add(每层的每个元素);
}
返回值.put(当前层数,每层集合);
当前层数++;
}
}
return 返回值;
}
}
3.2 深度优先搜搜
public static void 深度优先搜索(HashMap>> 图){
ArrayList 返回值=new ArrayList<>();
int 当前层数=1;
String 根节点=(String)图.get(当前层数).get(0).get("元素");
String 临时变量=根节点;
返回值.add(临时变量);
b:for (;;){
//节点是否有未被遍历过的儿子,且该儿子的父亲列表中的第一个父亲为自己?
boolean 前进条件1=false;
ArrayList 该节点的儿子列表=new ArrayList<>();
d:for (HashMap 每层的每个元素: 图.get(当前层数)) {
if((String)每层的每个元素.get("元素")==临时变量){
该节点的儿子列表=(ArrayList)每层的每个元素.get("儿子");
break d;
}
}
//ArrayList 该节点的儿子列表=(ArrayList)图.get(当前层数).get(0).get("儿子");
// System.out.println("当前节点:"+临时变量);
// System.out.println("当前节点的儿子:"+该节点的儿子列表);
a:for (String 每个儿子: 该节点的儿子列表) {
if(!返回值.contains(每个儿子)){
for (HashMap 每层的每个元素: 图.get(当前层数+1)) {
if((String)每层的每个元素.get("元素")==每个儿子&&
((ArrayList)每层的每个元素.get("父亲")).get(0)==临时变量){
前进条件1=true;
临时变量=每个儿子;
break a;
}
}
}
}
if(前进条件1){ //有
返回值.add(临时变量);
当前层数++;
continue b;
}else { //没有
//该节点是否有父亲?
boolean 前进条件2=false;
if(当前层数!=1){
c:for (HashMap 每层的每个元素: 图.get(当前层数)) {
if((String)每层的每个元素.get("元素")==临时变量){
前进条件2=true;
临时变量=((ArrayList)每层的每个元素.get("父亲")).get(0);
break c;
}
}
}
if(前进条件2){ //有
当前层数--;
continue b;
}else{ //没有
break b;
}
}
}
System.out.println(返回值);
}
3.3 广度优先搜索
public static void 广度优先搜索(HashMap>> 图){
ArrayList 返回值=new ArrayList<>();
for (int i = 1; i <=图.size() ; i++) {
if(i==1){
返回值.add((String)图.get(i).get(0).get("元素"));
}else{
Set 临时数组=new HashSet<>();
临时数组=(Set)图.get(i).get(0).get("本层所有元素");
for (String str: 临时数组) {
返回值.add(str);
}
}
}
System.out.println(返回值);
}
3.4 最小生成树
3.4.1 普利姆
public static void 普里姆(ArrayList 行,ArrayList 列,
ArrayList 关系,String 起始节点){
HashMap 返回值=new HashMap<>();
ArrayList 已使用的节点=new ArrayList<>();
已使用的节点.add(起始节点);
for(;;){
String 哪个已使用节点=null;
String 临时节点=null;
int 目前最小权值=0;
for (String 每个节点:已使用的节点) {
HashMap 和某个节点连接的所有节点=求和某个节点连接的所有节点(行, 列, 关系, 每个节点);
Set 所有节点=和某个节点连接的所有节点.keySet();
for (String str: 所有节点) {
if(!已使用的节点.contains(str)){
if(目前最小权值==0){
目前最小权值=和某个节点连接的所有节点.get(str);
临时节点=str;
哪个已使用节点=每个节点;
}else{
if(目前最小权值>和某个节点连接的所有节点.get(str)){
目前最小权值=和某个节点连接的所有节点.get(str);
临时节点=str;
哪个已使用节点=每个节点;
}
}
}
}
}
已使用的节点.add(临时节点);
返回值.put(哪个已使用节点+"-"+临时节点,目前最小权值);
if(已使用的节点.size()==行.size()){
break;
}
}
System.out.println(返回值);
}
3.4.2 克鲁斯卡尔
public static void 克鲁斯卡尔(ArrayList 行,ArrayList 列,
ArrayList 关系,String 起始节点){
}
3.5 最短路径
3.5.1 迪杰斯特拉
public static void 迪杰斯特拉(ArrayList 行,ArrayList 列,
ArrayList 关系,String 起始节点){
LinkedList 未遍历=new LinkedList<>();
HashMap 最短路径权值=new HashMap<>();
最短路径权值.put(起始节点,0);
HashMap> 最短路径路程=new HashMap<>();
ArrayList 初始最短路径路程值=new ArrayList<>();
初始最短路径路程值.add(起始节点);
最短路径路程.put(起始节点,初始最短路径路程值);
LinkedList 临时数组外部=new LinkedList<>();
临时数组外部.add(起始节点);
//初始化未遍历对象
for (String str: 行) {
未遍历.add(str);
}
while(未遍历.size()!=0){
System.out.println("临时数组外部"+临时数组外部);
ArrayList 临时数组内部=new ArrayList<>();
//临时数组内部需要排序
for (String str: 临时数组外部) {
未遍历.remove(str);
//111111111111111111111
HashMap 关系表=求和某个节点连接的所有节点(行,列,关系,str);
Set 关系表键集合=关系表.keySet();
System.out.println("str"+str);
System.out.println("关系表键集合"+关系表键集合);
//22222222222222222222
Set 最短路径权值键集合=最短路径权值.keySet();
for (String str2: 关系表键集合) {
System.out.println("aaaaa:"+str2);
System.out.println(最短路径权值键集合);
//3333333333333333
if(最短路径权值键集合.contains(str2)){
//55555555555555555555555555555
int 上面的值=最短路径权值.get(str)+关系表.get(str2);
int 下面的值=最短路径权值.get(str2);
//777777777777777777777
if(上面的值>下面的值){
}
//8888888888888888888888
else{
最短路径权值.put(str2,最短路径权值.get(str)+关系表.get(str2));
ArrayList linshi=new ArrayList<>();
for (String str3:最短路径路程.get(str)) {
linshi.add(str3);
}
linshi.add(str2);
最短路径路程.put(str2,linshi);
}
}
//4444444444444444
else{
//66666666666666666
最短路径权值.put(str2,最短路径权值.get(str)+关系表.get(str2));
ArrayList linshi=new ArrayList<>();
for (String str3:最短路径路程.get(str)) {
linshi.add(str3);
}
linshi.add(str2);
最短路径路程.put(str2,linshi);
临时数组内部.add(str2);
}
}
}
临时数组外部.clear();
for (String str4:临时数组内部) {
临时数组外部.add(str4);
}
}
System.out.println(最短路径权值);
System.out.println(最短路径路程);
}