Codeforces Round #631 (Div. 2) - Thanks, Denis aramis Shitov!

A. Dreamoon and Ranking Collection

**给出一个人参加n场比赛的所有排名，假设他再参加x场比赛可以取得v，v表示1~v的所有排名他都取得过，求最大的v（这道题读了好久才读懂… **
排名范围只有100，用数组标记枚举

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef pair<int,int> PII;
typedef long long LL;
int vis[1010];
int main(){
    int T;
    cin>>T;
    while(T--){
        int n,x;
        cin>>n>>x;
        memset(vis,0,sizeof vis);
        for(int i=1,x;i<=n;++i){
            cin>>x;
            vis[x]++;
        }
        int f;
        for(int i=1;i<1010;++i){
            if(vis[i]==0) {
                if(x==0) {
                    f=i-1;
                    break;
                }
                --x;
            }
        }
        cout<<f<<endl;
    }
    return 0;
}

B. Dreamoon Likes Permutations

求有多少种把一个序列从中间断开，得到两个从1开始的序列的方法

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef pair<int,int> PII;
typedef long long LL;
vector<int> v;
int vis[200010],a[200010];
int main(){
    int T;
    scanf("%d",&T);
    while(T--){
        int n;
        scanf("%d",&n);
        v.clear();
        memset(vis,0,sizeof vis);
        int Min=200010,Max=0;
        for(int i=1,x;i<=n;++i){
            scanf("%d",&a[i]);
            vis[a[i]]++;
        }
        int m1=0,m2=0,f=0;
        for(int i=n;i>=1;--i){
            if(vis[i]>0&&m1==0) m1=i;
            if(vis[i]==2&&m2==0) {
                m2=i;
            }
            if(vis[i]>2) f=1;
            if(m1!=0&&m2==0&&vis[i]!=1) f=1;
            if(m2!=0&&vis[i]!=2) f=1;
        }
        if(m1==0||m2==0||(m1+m2)!=n||f){
            cout<<0<<endl;
            continue;
        }
        memset(vis,0,sizeof vis);
        for(int i=1;i<=n;++i){
            int x=a[i];
            if(vis[x]) break;
            vis[x]++;
            Max=max(Max,x);
            Min=min(Min,x);
            if(Min==1&&(Max==m1||Max==m2)&&Max==i){
                v.push_back(i);
            }
        }
        cout<<v.size()<<endl;
        for(auto t: v){
            cout<<t<<" "<<n-t<<endl;
        }
    }
    return 0;
}

C. Dreamoon Likes Coloring

有m种颜色涂一个长度为n的方块，每种颜色涂连续$L_i$块，构造出使得所有方块都被涂色且每种颜色至少涂了一个方块的方法，方块上的颜色只记录最后一次涂的颜色
首先涂将每种颜色只涂一个头，最后从后向前向后调整让每个颜色尾部贴到最后，直到把全部覆盖

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef pair<int,int> PII;
typedef long long LL;
const int N=100010;
struct ac{
    int l,p;
}a[N];
bool cmp(ac a1,ac a2){
    return a1.l<a2.l;
}
int main(){
    int n,m;
    cin>>n>>m;
    long long sum=0;
    for(int i=1;i<=m;++i){
        cin>>a[i].l;
        sum+=a[i].l;
    }
    if(sum<n){
        cout<<-1;
        return 0;
    }
    for(int i=1;i<=m;++i){
        if(i+a[i].l-1<=n) a[i].p=i;
        else {
            cout<<-1;
            return 0;
        }
    }
    for(int i=m,rn=n;i>=1;--i){
        if(a[i].l+a[i].p-1<rn) {
            a[i].p=rn-a[i].l+1;
            rn-=a[i].l;
        }
        else break;
    }
    for(int i=1;i<=m;++i){
        cout<<a[i].p<<" ";
    }
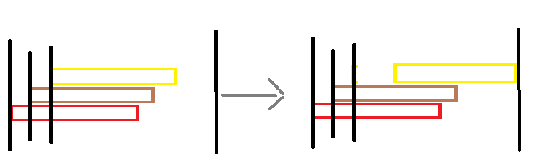
    return 0;
}

D. Dreamoon Likes Sequences

需要构造出一个数组a,满足存在一个数组b，b_i=b_i-1 xor a_i，a，b都是严格递增的且小于d，求出a的所有构造方案数
首先需要得到一个结论a是严格递增的，a的最高位1的位数也是单调递增的。即a_i-1i ，f(a_i-1)i)
数学归纳法证明：
b2=(b1 xor a2)>(a1 xor a2) , a2>a1
-> f(a2)> f(a1) f(b2)==f(a2)
证：a2>a1 -> f(a2)>=f(a1)
if：f(a2)==f(a1)，b2=(a1 xor a2)，f(b2) so：f(a2)>f(a1)

eg：b3=(b2 xor a3)，a3>a2
-> f(a3)>f(a2)
if：f(a3)==f(a2) ，f(a3)==f(b2)，b3=(b2 xor a3) ，f(b3） so：f(a3)>f(b2)==f(a2)
用记忆化搜索的方式存一下f[h,pos]，表示当前数列最后一个数的最高位1是h，数列长度是pos的构造方案数

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef pair<int,int> PII;
typedef long long LL;
const int N=40;
LL f[N][N],m,d;
LL dfs(int h,int pos){ //最后一个最高1位于为h,长度为pos
    if(f[h][pos]!=-1) return f[h][pos];
    LL ans=1;
    for(int i=h+1;1ll*(1<<i)<=d;++i){
        ans+=dfs(i,pos+1);
        ans%=m;
    }
    LL num=1<<h;
    if(1ll*(1<<(h+1))>d){
        num=d-num+1;
    }
    return f[h][pos]=(ans%m*num%m)%m;
}
int main(){
    int T;
    cin>>T;
    while(T--){
        memset(f,-1,sizeof f);
        cin>>d>>m;
        LL res=0;
        for(int i=0;1ll*(1<<i)<=d;++i){
            res+=dfs(i,1);
            res%=m;
        }
        cout<<res<<endl;
    }
    return 0;
}