在空间三维坐标系下的圆、直线和平面拟合
前言
上个学期,在做项目的时候遇到了许多需要拟合的情况。但是在网上寻找资料的时候大多是建立在二维空间的,在三维坐标系下的拟合较乱。因此在下面列举一些我所用到的直线拟合和圆拟合。
空间圆拟合
在二维空间中对圆的拟合较为简单,由初中的几何知识我们可以知道,确定一个三角形至少需要三个不共线的点,因此确定一个三角形的外接圆至少可用三个点。我们不妨假设三个点坐标为P1(x1,y1,z1),P2(x2,y2,z2),P3(x3,y3,z3)。
圆方程的标准形式为:
(xi-x)2+(yi-y)2=R2 (1)
在三维空间坐标系中球的方程为:
(xi-x)2+(yi-y)2+(zi-z)2=R2 (2)
一个空间圆的产生可以看作过该圆心的一个球体,被一个经过该点的平面所截而得到。因此在求取空间圆的时候还应添加平面约束方程,以上述P1、P2、P3三个不共线的点可以确定一个平面,平面方程为:
AX+BY+CZ+D=0 (3)
求解方程(3)时注意技巧,常用两种方式,向量法或者待定系数法。若使用待定系数法则需平面方程的另一种形式,点法式为:
A(x-x0)+B(y-y0)+C(z-z0)=0 (4)
但是笔者建议使用向量的方式,更为简单方便,三点在同一个平面上,以P1为基点,寻找两条向量P12、P13;该平面方程的法向量为n=P12×P13(注:向量的叉乘)。在得到平面的法向量之后,带入其中一个点到方程(4)中即可得到平面约束方程。我们不妨将该约束方程系数设为A1、B1、C1、D1。
在得到约束平面方程之后还须求解空间中圆的方程,在求解圆的方程时也有诸多方式,一种方式为将已知点带入到方程(2)中,利用待定系数法求解,我们仍参以P1为方程的基点,分别将P2,P3带入可以得到如下方程:
(x1-x)2+(y1-y)2+(z1-z)2=R2
(x2-x)2+(y2-y)2+(z2-z)2=R2
(x3-x)2+(y3-y)2+(z3-z)2=R2
整理后可以得到
A2=2(x2-x1) ,B2=2(y2-y1) ,C2=2(z2-z1),D2=x12+y12+z12-x22-y22-z22 (5)
A3=2(x3-x1) ,B3=2(y3-y1) ,C3=2(z3-z1),D3=x12+y12+z12-x32-y32-z32 (6)
建立系数矩阵:
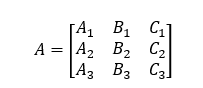

求解上述方程即可得到空间圆心坐标(x,y,z)另一种方式求解可以利用三角形外接圆的性质求解,该方式较为简单,我们知道三角形外接圆的圆心可以由三角形两边的垂直平分线交点确定,因此,可以通过该方式求解空间圆,由上述已知P1、P2、P3三点所在的平面方程,我们通过向量P12、P13能够求得该平面的法向量n,将法向量n分别与P12、P13叉乘,即可求得垂直于P12、P13的向量,不妨设为n12,n13,通过P1、P2求得P1P2边中点M(mx,my,mz),同理求得P1P3边中点N(nx,ny,nz)。
由于我们所求的是空间直线的交点,因此我们还应知道空间直线方程,在上述计算中,已经得到了两条垂直平分线的方向向量:n12,n13,不妨设n12(l,m,n)、n13(p,q,r)。
则两条空间直线方程可以写为
t = x − m x l = y − m y m = z − m z n t = \frac{x-m_x}{l}=\frac{y-m_y}{m}=\frac{z-m_z}{n} t=lx−mx=my−my=nz−mz
s = x − n x p = y − n y q = z − n z r s = \frac{x-n_x}{p}=\frac{y-n_y}{q}=\frac{z-n_z}{r} s=px−nx=qy−ny=rz−nz
联立方程消去xyz,可得到下列方程(不唯一)
l ∗ t + m x = p ∗ s + n x l*t+m_x=p*s+n_x l∗t+mx=p∗s+nx
m ∗ t + m y = q ∗ s + n y m*t+m_y=q*s+n_y m∗t+my=q∗s+ny
改写为矩阵形式

求解上述矩阵即可得到t,s,由直线的点向式和参数式子之间的转化可以得到
{ x = x 0 + l ∗ t , y = y 0 + m ∗ t , z = z 0 + n ∗ t \begin{cases}x=x_0+l*t , \\y=y_0+m*t , \\z=z_0+n*t \end{cases} ⎩⎪⎨⎪⎧x=x0+l∗t,y=y0+m∗t,z=z0+n∗t
将上述得到的t或者s和点带入即可得到垂直平分线交点坐标(x,y,z),即为空间三角形的外接圆圆心。
空间直线拟合(二乘法)
实现在二维平面的直线拟合较为简单,可以利用离散点(实际点)与拟合直线上的点(理想点)残差的平方和作为目标函数,求偏导计算最小值即可。另一种方式可以解多个点的矛盾方程,构建直线拟合经验公式:
y = a ∗ x + b y=a*x+b y=a∗x+b
在二维空间中,假设我们有一组二维点数据,其中每一个X均有一个Y与之对应,我们不妨构建矩阵
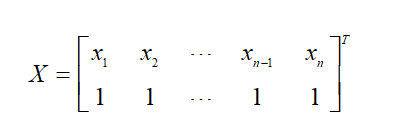

构建,矛盾方程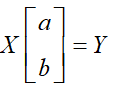 求解即可。
求解即可。
在三维空间之中,我们也可以使用解矛盾方程的方式求解,空间直线的标准方程为
x − m 0 m = y − m 0 n = z − m 0 p \frac{x-m_0}{m}=\frac{y-m_0}{n}=\frac{z-m_0}{p} mx−m0=ny−m0=pz−m0
等价转化之后
x = m p ( z − z 0 ) + x 0 = k 1 z + b 1 x=\frac{m}{p}(z-z_0)+x_0=k_1z+b_1 x=pm(z−z0)+x0=k1z+b1
y = n p ( z − z 0 ) + y 0 = k 2 z + b 2 y=\frac{n}{p}(z-z_0)+y_0=k_2z+b_2 y=pn(z−z0)+y0=k2z+b2
其中 k 1 = m p , b 1 = x 0 − m p z 0 , k 2 = n p , b 2 = y 0 − n p z 0 k_1=\frac{m}{p},b_1=x_0-\frac{m}{p}z_0,k_2=\frac{n}{p},b_2=y_0-\frac{n}{p}z_0 k1=pm,b1=x0−pmz0,k2=pn,b2=y0−pnz0
可以带入相应的点构件矛盾方程求解,或者利用残差的平方和求最小(笔者所用),构件目标函数如下:
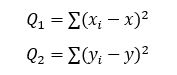
将x,y带入上面的方程,并对b,k分别求偏导可得到如下方程组
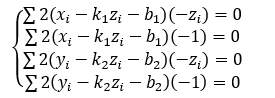
在计算上述方程式,要注意将求和符号的分解,求解计算得出k1,b1,k2,b2,将值返回方程
{ x = k 1 ∗ z + b 1 , y = k 2 ∗ z + b 2 \begin{cases} x=k_1*z+b1 , \\y=k_2*z+b2 \end{cases} {x=k1∗z+b1,y=k2∗z+b2
该方程即为拟合的空间直线方程。
实现上述过程在opencv或者Matlab中均十分简单,在此就不贴上自己拙劣的代码了。。。。。。
如有错误,欢迎指正。