《大数据》2015年第3期“研究”——社交网络影响力传播研究(上)
![]()
社交网络影响力传播研究
陈卫
(微软亚洲研究院 北京 100080)
摘 要:随着互联网和大数据的研究应用日益广泛,对社交网络影响力传播的研究成为数据挖掘和社交网络分析中的热点。从影响力传播模型、影响力传播学习和影响力传播优化3个方面总结了近些年计算机科学领域对影响力传播研究的主要成果,展示了影响力传播研究中对随机模型、数据挖掘、算法优化和博弈论等技术的综合运用。最后,简要讨论了影响力传播研究和应用中存在的问题、挑战及今后的研究方向。
关键词:社交网络;社会影响力;影响力传播模型;影响力最大化;社会影响力学习;病毒营销
doi: 10.11959/j.issn.2096-0271.2015031
Research on Influence Diffusion in Social Network
Chen Wei
(Microsoft Research Asia, Beijing 100080, China)
Abstract: With the wide spread of internet and big data research and applications, influence diffusion research in social network becomes one of the hot topics in data mining and social network analysis in recent years. The main results on social influence diffusion research from the field of computer science in the last decade, which covers the three main areas -- influence diffusion modeling,influence diffusion learning, and influence diffusion optimization, were summarized. Different techniques, such as stochastic modeling, data mining,algorithmic optimization, and game theory, were demonstrated in their application to influence diffusion research. Finally, some discussions on the current issues, challenges and future directions in influence diffusion research and applications were provided.
Key words: social network, social influence, influence diffusion model, influence maximization, social influence learning, viral marketing
论文引用格式:陈卫.社交网络影响力传播研究.大数据,2015031
Chen W. Researchon influence diffusion in social network. Big Data Research, 2015031
1 引言
任何社会性动物在个体与个体、群体与个体之间都存在着相互影响的关系,例如个体依从群体的行为会有利于猎食或减少被猎食的可能。而人类作为具有复杂交流手段的高级社会性动物,社会影响力在社会生活中更是无处不在。小到听一首歌曲、选一个餐馆,大到确定政治观点或买一处房产等,人们的各种选择和决定常常受家人、同事、朋友以及更广泛的大众倾向的影响。深入认识影响力的产生和传播模式有助于理解人类群体和个体的行为,从而能够预期人们的行为,为政府、机构、企业等各部门的决策提供可靠的依据和建议。比如企业在进行新产品推广时,可以利用对用户影响力及其传播的了解,选择有影响力的用户和传播渠道帮助产品推广,而政府可以选择合适的影响力群体和渠道来扩大其政策的影响或抵御谣言的传播。
社会影响力的研究在社会科学和市场学领域已有较长的历史[1,2],为影响力传播的途径和范围带来了新的认识。比如Christakis和Fowler利用美国一个城市上万人跨32年的医疗记录数据验证了肥胖症和吸烟行为会在社交网络中相互影响和传播[3,4]。而伴随着互联网、在线社交网络和大数据的兴起以及日益广泛的应用,在更大规模下更深入地研究影响力的传播也成为可能。比如近期基于著名的社交网站脸谱(Facebook)平台的两项研究,都通过在线随机试验方式分别验证了影响力在选举意愿和应用选择中的存在性及其决定性因素[5,6]。
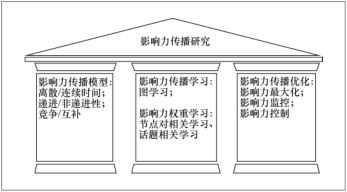
在计算机科学领域,基于互联网和大数据的影响力传播研究也从21世纪开始兴起。本文集中介绍这十几年来计算机科学领域在社交网络影响力传播方面的研究成果,并对面临的挑战和今后的方向加以简要讨论。概括来讲,影响力传播研究有三大支柱(如图1所示)。第一是影响力传播模型,主要描述影响力在社交网络中如何传播、有何特点和性质。第二是影响力传播的学习,即如何利用网络大数据挖掘学习影响力传播模式和具体传播模型的参数。第三是影响力传播优化,着重考虑在不同的传播模型下,如何通过施加外部作用(比如选取有影响力的初始传播用户和改变传播途径等)来扩大希望传播的影响力或者控制和减弱不希望传播的影响力,也包括有效地监控影响力的传播等。下文就分别对影响力传播的这三大支柱进行一一讲述。
影响力的研究和应用也是一个涵盖很广的课题,也有其他的综述型文章对其加以介绍[7,8]。与其他综述不同的是本文重点介绍对影响力动态传播特性的研究,而其他方面(如从静态图特性估计节点影响力等)请参见其他综述文章的相关介绍[7,8]。Chen、Lakshmanan和Castillo在近期发表了信息和影响力传播方面的专著[9],对影响力传播的研究有较详尽的介绍。本文对该专著覆盖的内容进行了提炼、概括,并包含了对该专著出版后的最新研究成果的介绍和一些新观点的讨论。
2 影响力传播模型
信息和影响力在社交网络中的传播复杂多样,但排除一些干扰因素后仍然有章可循。在下文中统一用影响力传播来概括在社交网络中信息、概念、想法、创新、产品、文化基因(meme)等的传播。
首先把一个社交网络描述成一个有向图G=(V,E),其中V是节点的集合,E⊆V×V是有向边的集合。每一个节点v∈V代表一个社交网络中的人,每一条边(u,v)∈E代表节点u到节点v的影响力关系。边是有向的,表明影响力是有方向的,节点u对节点v有影响力,但节点v对节点u可能没有影响力。在后面具体建模中还通常会对边加上权重以表示影响力的强度。对于一条有向边(u,v)∈E,它叫做节点u的出边,节点v的入边,节点v是节点u的一个出邻居,而节点u是节点v的一个入邻居。一个节点v的所有出邻居的集合用N+(v)表示,所有入邻居的集合用N-(v)表示。
通常情况下,针对某一具体传播的实体(信息、想法、产品等),将图中的每个点描述为两种可能状态:不活跃(inactive)和活跃(active)。不活跃状态表示该个体还没有接受对应实体(信息、想法或产品),而活跃状态表示该个体已经接受对应的实体。节点从不活跃状态变为活跃状态表示该节点接受了对应实体,也称之为被激活。
影响力传播模型用来刻画影响力在社交网络中的传播模式,也即社交网络中节点的状态如何影响其相邻节点的状态,并造成某一状态(通常指活跃状态)在网络中扩散传播。传播模型分很多种类,其中大多数以随机模型(stochastic models)来描述,也有用博弈论模型(game-theoretic models)来描述的。本文着重描述随机模型,因为它更直接地反映了影响力传播中的不确定性,也是当前研究的主流。
随机模型又可分为离散时间和连续时间模型、递进性(progressive)和非递进性(non-progressive)模型等。离散时间模型将影响力传播和节点的状态转换规定在离散的时间点发生,以便于计算和分析,而连续时间模型允许传播和节点状态转换在连续时间轴上发生。递进性模型假设任意节点一旦从不活跃变为活跃就会一直保持在活跃状态,不会再回到不活跃状态。这类模型多用于信息、产品等的传播,因为它们一旦拥有,就一般不会再失去,或者只关注传播过程中所有曾经接受该信息或产品的人群。非递进模型则允许节点在两个(或多个)不同状态之间来回切换。这类模型多用于描述观点、看法的传播,因为人的观点和看法经常会随着时间和周围人群的观点而改变。在这种情况下也许对状态的描述用支持、反对等词语比用不活跃和活跃更合适。在众多模型中,离散时间递进性模型是研究最多的。本文以介绍经典的离散时间递进性模型和其上的应用问题为主线,附带简略介绍其他模型。
2.1 经典离散时间递进性传播模型
影响力传播模型的研究在社会和管理科学中由来已久[1,2],但在计算机科学中基于计算和大数据的社交网络影响力传播模型的研究还是21世纪之后的事情。首先是Domingos和Richardson于2001年提出了基于马尔科夫随机场(Markov random field)的社交网络影响力模型[10]。严格地说,这个模型是关于图中节点被激活的相关性模型,而不直接表达影响力传播的因果关系。2003年,Kempe、Kleinberg和Tardos提出了独立级联(independent cascade)和线性阈值(linear threshold)等离散时间递进性传播模型和它们的若干拓展模型[11]。这些模型总结了前人在社会心理学、市场学及统计物理方面的模型,简单直观,基本符合人们对影响力传播的直觉理解,同时模型具有较好的性质,便于进一步分析和计算。这些模型如今已成为研究影响力传播的经典模型,被广泛应用到影响力最大化、影响力学习和影响力传播模型拓展等各个研究方面。下面对独立级联和线性阈值模型加以介绍,并在以后各部分中以独立级联模型为主要实例,介绍模型在各方面研究的应用。
2.1.1 独立级联模型
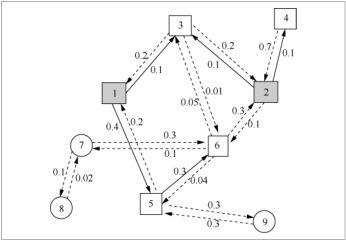
如图2所示,在独立级联模型中,每一条图中的有向边(u,v)∈E都有一个对应的概率值p(u,v)∈[0,1]。直观上说,p(u,v)表示当节点u被激活后,节点u通过边(u,v)独立激活节点v的概率。独立级联模型下的动态传播过程在离散时间点以如下形式完成:在t=0时刻,一个预先选好的初始集合S0首先被激活,而其他节点都处于不活跃状态。这个初始节点集合被称作种子节点集合(seedset)。对任何时刻t≥1,用St表示到这个时刻为止所有活跃点的集合。在任何时刻点t≥1,对任何一个在上一时刻刚被激活的节点u∈St-1\St-2(设S-1=φ),节点u会对它的每个尚未被激活的出邻居节点v∈N+(v)\St-1尝试激活一次,而这次尝试成功的概率为p(u,v),且这次激活尝试与所有其他的激活尝试事件相互独立。如果尝试成功,则节点v在时刻t被激活,即v∈St\St-1;如果尝试不成功,且节点v的其他入邻居也未在时刻t成功激活节点v,则节点v在时刻t仍为不活跃状态,即v∈V\St。当在某一时刻不再有新的节点被激活时,传播过程结束。
图2给出了独立级联模型一次传播结果的示意。实心方框表示种子节点,空心方框表示传播结束时被激活的节点;圆圈表示未被激活的节点;实线边表示影响力在该边上成功传播,虚线边表示影响力未在其上传播;边上的数字是该边上影响力传播的概率。在t=0时刻,种子节点1和2被激活;在t=1时刻,节点1、2分别激活节点5、4,并且同时激活了节点3;在t=2时刻,节点5成功激活节点6但没有成功激活节点9;在t=3时刻,节点6没有成功激活节点7;传播至此结束,节点7、8和9没有在这次传播中被激活。
用S∞表示在传播过程结束时所有活跃节点的集合。如果总节点数为n,而每一步至少激活一个新节点,则在这个模型下传播最多在n-1步后结束,即Sn-1=S∞。由于传播过程是随机过程,因此S∞是随机集合。在影响力传播中经常关心的是传播结束后被激活节点个数的期望值,即E[|S∞|],用σ(S0)表示,并称之为(最终)影响力延展度(influence spread)。
注意到在独立级联模型中,任何一个节点u对它的任何一个出邻居v只有一次尝试激活机会,且发生在节点u刚被激活的下一时刻。这看起来似乎是模型的一个局限。但如果只关心最终的影响力延展度,一个节点u在何时尝试激活另一节点v或者是否多次尝试激活节点v并不重要,只要用p(u,v)表示节点u多次尝试激活节点v的总成功概率,影响力延展度和引入多次激活尝试的扩展模型下的延展度是一样的[9]。如果要考虑中间某时刻的影响力延展度,也可将独立级联模型进行适当扩展,以使其更适合实际情况[12]。
独立级联模型抽象概括了社交网络中人与人之间独立交互影响的行为。它通过边上的概率来描述人与人之间发生影响的可能性和强度。很多简单实体(如新消息在在线网络的传播或新病毒在人际间的传播)很符合独立传播的特性[13]。独立级联模型也在基于实际数据的影响力学习中被初步验证是有效的。所以独立级联模型是目前研究最广泛、最深入的模型。
2.1.2 线性阈值模型
在线性阈值模型中,每条有向边(u,v)∈E上都有一个权重w(u,v)∈[0,1]。直观上说,w(u,v)反映了节点u在节点v的所有入邻居中影响力的重要性占比。要求∑u∈N-(v)w(u,v)≤1。每个节点v还有一个被影响阈值θv∈[0,1],这个阈值在0到1的范围内均匀、随机地选取,一旦确定在传播中就不再改变。与独立级联模型一样,在t=0时刻有且仅有种子集合S0中的节点被激活。在之后每个时刻t≥1,每个不活跃节点v∈V\St-1都需要依据它所有已激活的入邻居到它的线性加权和是否已达到它的被影响值来判断是否被激活,即是否满足∑u∈N-(v)∩St-1w(u,v)≤θv;若是,则节点v在时刻t被激活(v∈St);否则,节点v仍然保持不活跃状态。当某一时刻不再有新的节点被激活时,传播过程结束。
线性阈值模型中节点v的阈值θv表达了节点对一个新实体的接受倾向:阈值越高,节点v越不容易被影响;反之,阈值越低越容易被影响。节点v的入邻居对节点v的影响是联合发生的,可能任何一个入邻居都不能单独激活节点v,但几个入邻居联合起来就可能使对节点v的影响力权重超过节点v的阈值,从而激活节点v。这对应了人类行为中在面对一个相对复杂选择时(如购买新型手机、选择移民、参与暴乱等)经常出现的从众行为[2,13],也是与独立级联模型相比最主要的不同点。
线性阈值模型的随机性完全由节点被影响阈值的随机性所决定,一旦随机阈值被确定,后面的传播过程完全是确定性的。在线性阈值模型中阈值在0和1之间随机选取,这反映了对节点阈值的不了解。然而,在实际中人的被影响阈值虽然有随机性,但应该在更窄的范围内波动。另一方面,如果用更窄范围的随机阈值(如固定阈值)会使模型的分析和计算难度显著加大[9,11]。所以,线性阈值模型在阈值选取上面临两难选择,这也是这一模型不如独立级联模型应用广泛的一个原因。
2.1.3 独立级联和线性阈值模型的推广
Kempe等在独立级联和线性阈值模型的基础上又对其进行了推广[11],引入了诸如触发模型(triggering model)、通用级联模型(general cascade model)、通用阈值模型(general threshold model)等。总体来讲,是让独立级联模型中的独立概率或线性阈值模型中的线性权重变得更灵活、覆盖更广的传播形式。由于篇幅关系,在这里不再展开介绍。感兴趣的读者请看原文或相关综述[9,11]。
2.2 其他传播模型
除了上文介绍的离散时间递进性经典模型,根据不同实际需要还有很多其他模型,用来刻画社交网络中信息和影响力的传播。在这里只做简要介绍。
2.2.1 连续时间模型
连续时间模型(continuous-time model)将网络中两个相连节点的传播时延用一个连续时间的密度函数表示,这样节点的激活可以在任何连续时间内发生[14]。这个模型避免了对实际数据离散化分段,在数据分析时经常是一种有效模型。现在的研究大多是对独立级联模型的连续化,对线性阈值模型的连续化还有待进一步研究。
2.2.2 传染病模型
顾名思义,传染病模型(epidemic model)集中研究传染病或病毒在人群中的传播[15],现在也被延伸用来研究信息和影响力传播。经典传染病模型将人的状态分为几类,比如易感S(susceptible)、感染I(infected)、治愈R(recovered)等。然后,根据可行的状态转换定义出不同的模型,如SI模型描述人从易感变为感染;SIS模型允许人从感染回到易感状态然后再被感染;SIR模型刻画人从易感变为感染然后再痊愈并永久免疫的情况。传染病模型有考虑人群整体行为的,也有基于人际之间接触网络的。前面介绍的独立级联模型与SIR模型在网络中的传播基本具有相同的性质。
2.2.3 选举模型
选举模型(voter model)原是统计物理里一个常用的模型,现在也被用到社交网络影响力传播的研究中[16,17]。在最基本的选举模型中每个节点有两个状态,每个节点u在每个离散时刻从它的邻居节点中随机挑选一个节点v,将节点v在上一时刻的状态作为自己的当前状态。这一过程类似于社交网络中人们通过和朋友交流而采纳朋友意见的过程,所以选举模型和它的变种常用来刻画人们的看法、意见等在社交网络中的演变。因为节点的状态可在多个状态中反复变化,所以选举模型属于非递进性模型,一般用于分析在某一时间点或稳态下的状态分布和相关性质。
2.2.4 博弈论模型
博弈论模型(game-theoretic model)将每一个节点描述为利益最大化的自私节点,其状态就是它的博弈策略。用于刻画传播的网络博弈论模型经常将每条边描述为其两个顶点的一个协调博弈(coordination game),当两个顶点选取同一策略时各自的收益都最大[18,19]。这种模型反映了人际之间的趋同效应和某些产品的网络外部效应(network externality),比如双方都用Skype作为网络通信工具对双方都有益处。这种模型在某节点的一次状态转换过程类似于阈值模型,而状态的反复交替又与选举模型有类似性质。
2.2.5 多实体传播模型
在网络中很可能有多个实体同时传播它们的影响力,它们之间有可能是相互竞争的关系(比如小米手机和iPhone,或者关于某热点事件的官方消息和谣言等),也有可能是互补合作关系(比如iPhone和Apple Watch、微软视窗操作系统和联想笔记本电脑等)。多实体的传播会造成更复杂的传播现象和结果。近几年,已有不少工作着眼于将单实体传播模型(如独立级联和线性阈值模型)扩展为多实体传播模型(multi-item diffusion model)[9,20~24]。绝大多数扩展模型只考虑竞争性实体的并发传播。这些扩展在网络传播上基本继承单实体的传播模型,但在节点上设置先来先用、后来放弃的规则,并辅以同时到达时的打破平局(tie-breaking)规则。Lu等人最近将多实体的竞争性模型又进一步扩展为既可以描述竞争也可以描述互补合作的比较影响力传播模型(comparative influence diffusion model)[24]。该模型利用节点自动机和少数几个参数刻画了节点在接受一个实体前后会接受另一个实体的不同概率。参数的不同取值范围可以囊括从完全竞争到部分竞争、相互独立、部分互补和完全互补的各种可能情况。总的来说,由于多实体传播模型引入了更复杂的交互和传播机制,模型的性质分析和其上的优化问题等也变得更为复杂。
3 影响力最大化问题
影响力传播建模的一个主要目的是控制和优化影响力的传播,这其中被广泛研究的一个核心问题就是影响力最大化(influence maximization)问题。本节以独立级联和线性阈值模型为基础,介绍影响力最大化的研究技术和主要成果,并附带介绍其他影响力传播中的优化问题。
3.1 影响力最大化问题的定义
影响力最大化是在给定社交网络结构G=(V,E)、影响力传播模型及其参数(如独立级联模型和边上的概率)的情况下,选择k个节点作为种子节点集合S*,使得以S*为种子节点产生的影响力延展度σ(S*)最大,即S*=argmaxS⊆V, |S|=kσ(S)。
影响力最大化问题是对病毒营销(viral marketing)的一个直接数学刻画。比如一个厂家要推广产品,希望用病毒式营销手段,先选择网络中少数人送以免费试用产品,希望选中的人试用以后喜欢新产品并主动在其朋友圈推广,使得更多的人接受和购买该产品,而这些新用户又会在他们的朋友圈中进一步推广该产品。厂家的期望是,基于对网络中影响力传播的了解(参见第4节影响力传播学习),能够找出接受试用产品的最佳用户(种子节点),使得最终接受产品的人最多(影响力延展度最大)。这个问题正是影响力最大化的优化目标。
3.2 子模函数(submodular function)和影响力最大化的贪心算法技术
上述影响力最大化问题属于组合优化问题,更具体地说,影响力最大化在经典的独立级联和线性阈值模型下都属于图上覆盖问题的一种扩展,因而与图覆盖问题一样,在这些模型下影响力最大化是NP难的问题。解决NP难优化问题的一个重要方法是利用有效的近似算法,比如即使找不到使影响力延展度达到最大的种子集合,但可能找到一个较好的集合,使得该集合的影响力延展度接近最优值,而两者之间的比例就是近似算法的近似比。影响力最大化的近似算法设计核心依赖于影响力延展度函数的子模性质和其带来的贪心算法技术。
对于一个将有限集合V的任意子集映射到实数值的函数f:2V→R,称f满足子模性,对于任意一个子集S⊆V和它的任意一个超集T(S⊆T⊆V)以及T外的任意一个元素u∈V\T,f满足f(S∪{u})-f(S)≥f(T∪{u})-f(T)。子模性反映了元素u在集合S基础上的增量效应随着S的增大而递减,这就是在经济学中经常用到的边界效用递减现象。很多图覆盖问题都具有子模性,因为覆盖的重叠现象会造成边界效用递减。重要的是,影响力延展度作为种子集合的函数σ(S)已被证明在独立级联和线性阈值模型以及它们的很多扩展模型下都满足子模性[11]。
和子模性经常在一起使用(但非绝对必要)的还有集合函数的单调性,称集合函数f满足单调性,对于任意一个子集S⊆V和它的任意一个超集T(S⊆T⊆V),f满足f(S)≤f(T)。影响力延展度函数σ(S)同样具有单调性。
一个单调子模函数的重要性质是可以用如下的贪心算法得到函数最大值的近似解。
算法:单调子模函数的贪心算法。
输入:单调子模函数f,预算k。
输出:大小为k的子集S。
初始化: S= φ
fori =1 to k do
v=arg max u∈V\S (f(S∪{u} )-f(S) )
S=S∪{v}
endfor
返回S
贪心算法分k轮,每一轮都要找到一个元素,使得它对已找到的元素来说边界增量最大。如果f是单调子模的,且f(φ)=0,则贪心算法找到的贪心解保证至少是最优解的(1-1/e),即大约63%[25]。所以贪心算法是单调子模函数最大化的(1-1/e)的近似算法。
由于影响力延展度函数σ(S)在独立级联和线性阈值模型下都具有单调性和子模性,且显然σ(φ)=0,所以可以用贪心算法来解决影响力最大化问题,以达到的(1-1/e)近似比。
3.3 可扩展的影响力最大化算法
然而,第3.2节给出的单调子模函数的贪心算法并未完全解决影响力最大化问题,因为其中的关键一步需要计算一个种子集合S的延展度σ(S),而计算σ(S)的精确值本身在独立级联和线性阈值模型下都是很难的问题(技术上称为NP难问题[26,27])。在Kempe等人的论文中[11],简单地提出用随机模拟的方法(通称蒙特卡洛方法)来模拟影响力传播,从而估算σ(S)的近似解。在这种近似解情况下,贪心算法的解能达到的(1-1/e-ε)近似解,其中ε是一个大于零的数,对应σ(S)估算的精确性。
但是简单地在影响力最大化中用蒙特卡洛方法有一个严重的问题,就是时间效率很低。在一个不算大的上万个节点的图中,如果对每一次延展度估计都用并不算多的2 000次蒙特卡洛模拟,找出50个种子节点的贪心算法要运行好几天[9]。为了解决这个效率问题,诸多研究提出了各种可扩展的影响力最大化(scalable influence maximization)算法。这些算法基本可分为两大类,一类是利用模型具体特点的启发式算法[26~30],另一类是改进蒙特卡洛方法的贪心近似算法[31~35]。
在启发式算法中,PMIA是一个有代表性的针对独立级联模型的算法[26]。PMIA的主要思想是将在一般图上针对某一节点影响力的传播转化为在该节点附近区域的一棵有代表性的最大影响力传播子树上的传播。这样做的好处是:独立级联模型的影响力延展度计算在树结构上可在线性时间内完成;构造以某一节点为中心的最大影响力子树(maximum influence arborescence)可以用Dijkstra最短路径算法在近线性时间完成;只考虑节点附近的子树会大大减少计算量,同时又不会损失太多计算精度,因为影响力在几步传播后已变弱到可以忽略不计。PMIA和当时已做过优化的蒙特卡洛贪心算法相比,速度提高了1 000倍,而选出种子的影响力在很多实际网络的模拟实验中都很接近贪心算法。之后,又有不少工作对算法做了进一步改进和提高,比如IRIE算法利用图上整体迭代方法提高了算法速度,同时节省了内存使用[30]。针对线性阈值模型也有LDAG算法[27]和SIMPATH算法[29]。这些算法的优点是速度很快,通常效果也很好,但它们缺乏理论保证,所以究竟它在哪些实际网络中适用,还有待进一步论证。
在对蒙特卡洛贪心算法的改进方面,一种改进是依据延展度函数的子模性利用偷懒估值方法(lazy evaluation)减少对函数估值的次数,如CELF算法[32]。单纯用这种方法虽然对最原始的蒙特卡洛方法有上百倍的提高(运行时间从几天降低到几个小时),但与高效的启发式算法相比还有上千倍的差别(几小时和几秒钟的差别)。最近,由Borgs等人率先提出的反向蒙特卡洛算法改变了这种局面[31]。反向蒙特卡洛算法的核心思想是不从种子节点去模拟估算种子节点的影响力,而是随机选取图上节点,从该节点出发以所有边的相反方向进行蒙特卡洛模拟,得到的集合实际上是最可能影响该节点的集合。这样的集合被称作反向可达集合(reserve reachabl set),简称RR集合。而如果一个节点经常在RR集合中出现,那么该节点就是一个影响力大的节点。基于这种思想,Borgs等人理论上证明了他们的算法可达到近乎最优的近线性时间,同时仍有(1-1/e-ε)的近似比保证。之后Tang等人对他们的算法加以改进,提出了TIM/TIM+和IMM算法[33,34],并进行了模拟实验验证,最新的IMM算法在实验中已超越了启发式算法(如IRIE、SIMPATH)的速度,同时仍有一定的理论保证(ε=0.5,所以理论保证较弱,但对任意图适用)。同时他们指出这种方法适用于独立级联、线性阈值和更广的触发模型。但基于RR集合的这些算法有一个问题是,当选出k个种子节点时,算法并不保证也同时找到所有小于k个种子集合的近似解。Cohen等人提出的SKIM算法避免了这个问题[35]:SKIM算法通过刻画节点在随机意义下的可达性草图(reachability sketches)来高效计算节点影响力和选择种子节点。理论上,SKIM算法不保证近线性时间但有近似比保证;实验上,它与TIM/TIM+相当。
3.4 其他基于影响力的优化问题
基于影响力传播还可以提出很多的优化问题或对模型的拓展。这仍然是现在学术界十分活跃的领域。下面简要介绍一下这方面的几个问题和相关研究。
(1)种子集合最小化
种子集合最小化是影响力最大化的对偶问题。它要求影响力延展度达到一定数值情况下选取的种子集合尽量小。这个问题的解法也是基于单调子模函数的贪心算法,但由于优化目标变为最小化种子集合的大小,近似比变为了O(lnη),其中η是影响力延展度要求达到的阈值[36,37]。
(2)利润最大化
利润最大化考虑到选取种子有成本,而被影响的非种子节点才会产生收益。所以,利润最大化的目标是选取合适的种子节点(不再受硬性的个数限制),使得最终的期望收益减去种子成本最大。与影响力最大化相比,利润最大化的一个重要区别是它的目标函数(即给定种子集合下的期望利润)不再是单调的。因为当种子集合达到一定程度时,再加一个节点作为种子带来的额外期望收益可能已经不能抵消加入这个种子的费用,但是利润函数仍具有子模性,在这种情况下,利润最大化要利用非单调子模函数的优化技术[38]。
(3)影响力传播监控
影响力传播可能达到网络的各个角落,如何布置有效的监控节点对各种影响力传播提供及时、准确的报告,也是一个重要课题。在技术层面,选择有效的网络监控节点和选择有效的种子节点有相似性,在适当的模型和问题描述下都具有单调性和子模性,所以都可以用贪心算法来解决[32]。
(4)多实体传播模型下的影响力最大化
多实体的传播会给影响力优化带来很多变种。比如在已知一个竞争实体分布的种子节点情况下,如何选取我方的种子节点从而最大化我方的影响力[9]或者尽量减少对方的影响力,也称为影响力阻断最大化(influence blocking maximization)[20,22]。影响力阻断最大化可以应用在抵御谣言的传播。也有学者研究社交网络平台在有多个竞争实体下如何公平分配种子资源的问题[23]。Lu等人在他们最新的研究中还考虑了在互补性实体间的影响力最大化问题[24],比如在已知一个互补实体的种子节点情况下,如何选取本方实体的种子节点以最大化本方的影响力(即自我影响力最大化(self influence maximization))或者最大化互补的对方的影响力(即互补影响力最大化(complementary influence maximization))。可以看出,多实体传播下的影响力最大化种类繁多,具体应用要具体分析。绝大多数问题仍然基于子模函数的最大化,但是多实体模型在不少情况下不再具备子模性,所以需要寻找新的解决途径。
(5)网络拓扑的优化
影响力传播研究中,也有研究如何有效地改变网络拓扑结构来优化影响力的。比如如何有效删除图中的边或节点使得种子节点的影响力尽量小,这对应了防止传染病传播中的隔离和免疫措施。也可以考虑如何增加点或边以最大化影响力,这在一定程度上对应了社交网络平台朋友推荐的情形。Khalil等人针对一种拓扑变化下定义的目标函数,论证了它的子模性或对称的超模性(supermodularity),从而用子模或超模函数的优化技术进行处理[39]。值得一提的是,他们定义的一个集合的影响力并不是集合整体的影响力延展度,而是集合中每个个体的影响力延展度的算术平均。这个定义使得他们能够得到对应的子模或超模性结论,但这样的模型只适用于单一种子从种子集合中随机选取的情形。
(6)非子模性的影响力优化问题
当对影响力传播模型进行一定扩展或对优化目标进行一定改变后,新的模型或问题经常就不再具有子模性(或超模性)。在最近的研究中对非子模性的影响力优化问题也提出了一些解决方法,比如利用整数规划[40],将其转化为相近的子模问题[41],假设图的一部分对应的带权重的邻接矩阵有常数秩[42],将非子模函数夹于两个子模函数之间的三明治方法[24]或者利用基于传播模型的启发式算法[43]。这些方法对某些具体问题有较好的效果,但非子模性的影响力优化问题的系统性研究还有待完善。
影响力传播中还有很多其他相关问题和相关算法,受篇幅限制,本文不能面面俱到。
![]()