【2.1】 数学建模值之TOPSIS(优劣解距离模型)的具体算法步骤详解
- 一、回顾层次分析法的局限性
- 二、topsis模型的介绍
- 三、模型的具体算法步骤
- 四、该模型的两个注意点
一、回顾层次分析法的局限性
- 评价的决策层不能太多,太多的话n会很大,判断矩阵和一致矩阵差异可能会很大
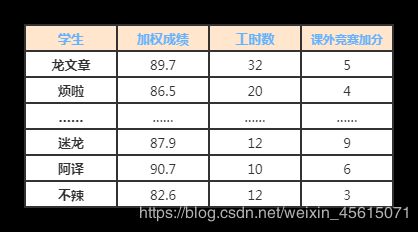
- 如果决策层中指标的数据是已知的,那么我们如何利用这些数据来使得评价更加准确呢(就是每个方案层关于各指标的得分已知,不用通过判断矩阵去求具体的结果)
二、topsis模型介绍
TOPSIS法是一种常用的综合评价方法,其能充分你利用原始数据的信息,其结果能够精确地反映各评价方案之间的差距
该模型的基本过程是:先将原始数据矩阵统一指标类型(一般正向化处理,即指标的值越大,代表对象本身越好),得到正向化矩阵,在对正向化矩阵进行标准化处理以消除个指标量纲的影响,并找到有限方案中的最优方案和最劣方案,然后分别计算个评价对象与最优方案和最劣方案间的距离,获得各评价对象与最优方案的相对接近程度,以此作为评价优劣的依据。该方法对数据的分布及样本的含量没有严格的限制,数据计算也较为简单。
三、具体模型算法的步骤
第一步:将原始矩阵正向化
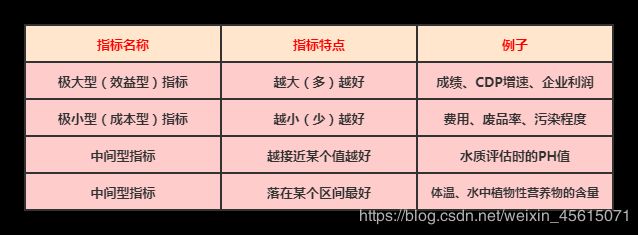
原始矩阵正向化:就是要将所有的指标类型统一转为极大型指标。(不同类型的指标进行转换的函数也不一样,具体见下一小节的讲解)
第二步:将正向化后得到的矩阵标准化
目的:消除指标不同量纲的影响
具体标准化过程的数学表示如下:
假设有n个要进行评价的对象,m个评价指标(已经通过第一步进行了正向化)得到的正向化矩阵如下:
X = [ x 11 x 12 ⋯ x 1 m x 21 x 22 ⋯ x 2 m ⋮ ⋮ ⋱ ⋮ x n 1 x n 2 ⋯ x n m ] X=\left[ \begin{matrix} x_{11}& x_{12}& \cdots& x_{1m}\\ x_{21}& x_{22}& \cdots& x_{2m}\\ \vdots& \vdots& \ddots& \vdots\\ x_{n1}& x_{n2}& \cdots& x_{nm}\\ \end{matrix} \right] X=⎣⎢⎢⎢⎡x11x21⋮xn1x12x22⋮xn2⋯⋯⋱⋯x1mx2m⋮xnm⎦⎥⎥⎥⎤
那么对矩阵X进行标准化后得到的新的矩阵记为Z,Z中的每一个元素的计算方法如下:
Z i j = x i j ∑ i = 1 n x i j 2 Z_{ij}=\frac{x_{ij}}{\sqrt{\sum_{i=1}^n{x_{ij}^{2}}}} Zij=∑i=1nxij2xij
Z i j = X 中的每一 个 元素 X 中该元素 所 在列 所 有元素的平方和 Z_{ij}=\frac{X\text{中的每一}个\text{元素}}{\sqrt{X\text{中该元素}所\text{在列}所\text{有元素的平方和}}} Zij=X中该元素所在列所有元素的平方和X中的每一个元素
第三步:计算得分并对结果进行归一化
假设有n个评价的对象,m个评价指标的标准化后的矩阵为Z,如下所示:
Z = [ z 11 z 12 ⋯ z 1 m z 21 z 22 ⋯ z 2 m ⋮ ⋮ ⋱ ⋮ z n 1 z n 2 ⋯ z n m ] Z=\left[ \begin{matrix} z_{11}& z_{12}& \cdots& z_{1m}\\ z_{21}& z_{22}& \cdots& z_{2m}\\ \vdots& \vdots& \ddots& \vdots\\ z_{n1}& z_{n2}& \cdots& z_{nm}\\ \end{matrix} \right] Z=⎣⎢⎢⎢⎡z11z21⋮zn1z12z22⋮zn2⋯⋯⋱⋯z1mz2m⋮znm⎦⎥⎥⎥⎤
一些得到计算结果的中间参数定义如下
定义最大值:
Z + = ( Z 1 + , Z 2 + , ⋯ , Z m + ) Z^+=\left( Z_{1}^{+},Z_{2}^{+},\cdots ,Z_{m}^{+} \right) Z+=(Z1+,Z2+,⋯,Zm+)
= ( max { z 11 , z 21 , ⋯ , z n 1 } , max { z 12 , z 22 , ⋯ , z n 2 } , ⋯ , max { z 1 m , z 2 m , ⋯ , z n m } ) =\left( \max \left\{ z_{11},z_{21},\cdots ,z_{n1} \right\} ,\max \left\{ z_{12},z_{22},\cdots ,z_{n2} \right\} ,\cdots ,\max \left\{ z_{1m},z_{2m},\cdots ,z_{nm} \right\} \right) =(max{z11,z21,⋯,zn1},max{z12,z22,⋯,zn2},⋯,max{z1m,z2m,⋯,znm})
定义最小值:
Z − = ( Z 1 − , Z 2 − , ⋯ , Z m − ) Z^-=\left( Z_{1}^{-},Z_{2}^{-},\cdots ,Z_{m}^{-} \right) Z−=(Z1−,Z2−,⋯,Zm−)
= ( min { z 11 , z 21 , ⋯ , z n 1 } , min { z 12 , z 22 , ⋯ , z n 2 } , ⋯ , min { z 1 m , z 2 m , ⋯ , z n m } ) =\left( \min \left\{ z_{11},z_{21},\cdots ,z_{n1} \right\} ,\min \left\{ z_{12},z_{22},\cdots ,z_{n2} \right\} ,\cdots ,\min \left\{ z_{1m},z_{2m},\cdots ,z_{nm} \right\} \right) =(min{z11,z21,⋯,zn1},min{z12,z22,⋯,zn2},⋯,min{z1m,z2m,⋯,znm})
定义第i(i = 1,2,…,n)个评价对象与最大值的距离为:
D i + = ∑ j = 1 m ( Z j + − z i j ) 2 D_{i}^{+}=\sqrt{\sum_{j=1}^m{\left( Z_{j}^{+}-z_{ij} \right) ^2}} Di+=j=1∑m(Zj+−zij)2
定义第i(i = 1,2,…,n)个评价对象与最小值的距离为:
D i − = ∑ j = 1 m ( Z j − − z i j ) 2 D_{i}^{-}=\sqrt{\sum_{j=1}^m{\left( Z_{j}^{-}-z_{ij} \right) ^2}} Di−=j=1∑m(Zj−−zij)2
利用这些中间参数可以计算出第i(i = 1,2,…,n)个评价对象未归一化后的评价得分:
S i = D i − D i + + D i − S_i=\frac{D_{i}^{-}}{D_{i}^{+}+D_{i}^{-}} Si=Di++Di−Di−

很明显 0 < S i < 1 , 且 S i 越大 D i + 越小,说明越接近评价得分的最大值 \text{很明显}0
四、 两个注意点:
- 要区别开归一化和标准化两个过程。对最终评价得分结果进行归一化也可以达到消除量纲影响的结果。但更多的时候,进行归一化的目的是为了让结果更加容易解释,或者说让结果有一个更加清晰直观的印象。
- 这里介绍的优劣解距离法没有对指标权重进行考虑,后面小节该模型的拓展讲解会示意加入指标权重之后,如何进行评价结果的计算
更多有关与TOPSIS模型的经典获奖论文,以及建模论文模板等资料关注公众号,回复,“TOPSIS”,即可免费领取!!!
![]()