《Robust Face Recognition via Sparse Representation》论文翻译

摘要——我们考虑了自动识别有着不同的表情、光照、以及遮挡和伪装的正面人脸存在的问题。我们把这类识别问题描述为一个多线性回归模型中的分类问题，并且认为来自稀疏信号表示的新理论为这类问题提供了解决办法。基于由$l^1$最小化计算的稀疏表示，我们提出了一个通用分类算法用于目标识别（基于图像）。这个新的框架为两个人脸识别领域的关键课题（特征提取和对遮挡的鲁棒性）上提供了更好的见解。对于特征提取，我们证明了如果识别问题中的稀疏性能够被合理利用的话，特征的选择也就不再至关重要了。而真正重要的问题是：特征数是否足够大、稀疏表示是否被正确计算。根据稀疏表示理论的预测，只要特征空间维度超过一定阈值，非传统的特征（比如下采样图像（downsample images）和随机投影（random projection））和传统的特征（比如Eigenfaces和Laplacianfaces）表现得一样好。由于遮挡和腐蚀而导致的误差关于标准（像素）正交基通常是稀疏的，因而这个框架可以一致的处理这些误差。稀疏表示的理论能够帮助预测识别算法可以处理多大面积的遮挡以及怎么选择训练图像才能最大化遮挡条件下的鲁棒性。为了证实所提出的算法的有效性和验证以上的结论，我们在公共数据库上进行了大量的实验。
关键字：人脸识别、特征提取、遮挡和腐蚀（corruption）、稀疏表示、压缩感知、$l^1$最小化、验证和异常值拒绝

1 引言

  简约法（parsimony）作为推理的一个指导原则已经有非常久远的历史了。一个最有名的例子就是在模型选择[1],[2]中的最小描述长度准则（MDL），它明确提出，在模型类的一个层次中能生成最紧凑表示的模型应该更适用于要做出决策的任务，比如分类。高维数据处理中的一个相关但是更简单的简约法是挑选那些只依赖于少数观察的模型，这些模型只选择一个特征的较小子集来进行分类和可视化（比如稀疏PCA[3],[4]和其他）。这种稀疏特征选择方法，在某种程度上等同于[5]和[6]中的支持向量机方法（SVM）。SYM选择相关训练样本的一个较小子集来描述类之间的决策边界。虽然这些工作仅仅包括一小部分用于推理的简约法文献，但它们确实致力于阐述一个共同的主题：它们都是用简约法作为一个原则来从训练数据中选择一个有限制的特征子集或者模型，而不是直接使用训练数据对输入（测试）信号进行表示或者是分类。
  简约法在人类感知中的作用也得到了人类视觉研究结果的强烈支持。研究者们最近发现，在中低水平的人类视觉功能中，视觉皮层的许多神经元对于各种具体的刺激，比如说颜色，纹理，方向，尺度甚至是视角不同的物体图像，具有选择性。考虑到这些神经元在每一个视觉阶段能形成一个关于基础信号元素的过完备字典，这些神经元关于给出的输入图像的激励过程是高度稀疏的。
  在统计信号处理领域，根据基本元素或者信号原子的一个过完备字典计算稀疏线性表示的算法问题已经成为最近的研究热点[9],[10],[11],[12]。大部分研究热点都围绕着一个发现，即任何时候只要最优表示足够稀疏，它就能够通过凸优化有效的计算[9]，即使在通常情况下此类问题很难解决[13]。由此引发的优化问题和统计学中的Lasso方法[12]相似，[14]惩罚了线性组合中系数的$l^1$范数，而不是直接惩罚非零系数的个数（比如$l^0$范数）。
  这些工作的初始目标本质上并不是推理和分类，而是利用可能比香农-奈奎斯特采样定理限制值的更低的采样频率对信号进行表示和压缩[14]。因此算法的效果可以根据表示的稀疏性和原始输入的保真度来衡量。此外，字典中单个的基本元素并不会有任何特别的语义，它们都是从标准基（比如傅里叶、小波、Curvelet、Gobor）中选出的，甚至是从随机矩阵[11],[15]中生成。然而，最稀疏的表示自然具有判别力：在基向量的所有子集中，它选择能够最紧凑表示输入信号的子集，并且拒绝其他所有可能没有那么紧凑的表示子集。
  本文中，我们提出了系数表示的自然判别性来进行分类。我们用一个基本元素是训练样本自身的过完备字典来表示测试样本，而不是用上述提到的一般的字典。如果每个类的训练样本足够多，就有可能将测试样本表示为来自同一类的训练样本的线性组合。这个表示自然是稀疏的，因为表示集只包含了总体训练数据的一小部分。在很多有趣的问题上，我们提出，测试样本在在过完备字典上的最稀疏线性表示可以有效利用$l^1$最小化得到。寻找最稀疏表示，从而在训练集中不同的类找出测试样本所属的类。图1用人脸识别作为一个例子阐述了这个简单的想法。稀疏表示也提供了一个简单但是及其有效的的方法来拒绝不属于训练数据中任何类的无效测试样本：这些样本的最稀疏表示往往包含跨越多个类的大量字典元素。

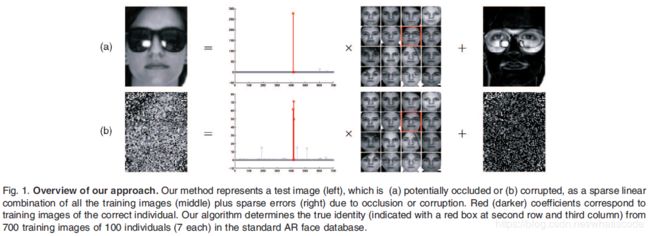
  我们对用来分类的稀疏性的使用和上述提到的各种简约法则有着显著的不同。我们的方法把每个单独测试样本的稀疏表示直接用于分类，并自适应的挑选有着最紧凑表示的训练样本，而不是使用稀疏性来得到一个之后能够用来区分所有测试样本的相关模型或者特征。已经提出的分类器可以被归纳为两种流行的分类器：NN（nearest neighbor）[18]和NS（nearest subspace）[19]（子空间中关于来自每一个目标类的所有训练样本的最小距离）。NN分类器是基于单个训练样本的最好的表示来区分测试样本的，而NS是基于每一类所有训练样本的最好的线性表示来分类。NFL（nearest feature line）算法[20]是NN和NS两个极端的折中办法，基于一部分训练样本的最好的仿射表示来进行分类。我们的方法同样也是折中，但却考虑了所有可能的支集（在每一个类中或者交叉在多个类中）并且自适应的选择了所需的最小数量的训练样本来表示每一个测试样本。
  我们将在自动人脸识别的环境下激励和研究这个分类的新方法。人脸无疑是基于图像的识别领域中最广泛的研究对象。这在一定程度上是由于人类视觉系统的卓越的人脸识别能力[21]以及人脸识别技术的广泛而又重要的应用[22]。除此之外，与人脸识别相关的技术问题一般而言就是目标识别和数据分类的代表。反过来，稀疏表示和压缩感知理论使得我们对自动人脸识别中两个关键课题上有了更深的理解，这两个关键问题分别是：特征提取的作用以及由于遮挡所导致的困难。
  特征提取的作用。“一个目标图像的哪个低维特征对于分类是最有价值的或者能提供最多信息？”这个问题通常是人脸识别以及目标识别的中心问题。已经有大量的文献致力于研究各种依赖数据的特征变换，用于把高维测试数据投射到低维特征空间：比如Eigenfaces[23]，Fisherfaces[24]，Laplacianfaces[25]以及许多变种（variants）[26]，[27]。对于这么多已经提出的特征，孰好孰坏几乎没有一致的看法，使用者们缺乏指导原则来决定使用哪一个特征。然而，在我们提出的框架中，压缩感知理论表明：具体选择哪一个特征空间已经变得不再至关重要。甚至随机的特征也包含了足够的信息来获得稀疏表示，从而能够正确的区分任何测试图像。特征空间的维度是否足够大才是关键的，只有这样稀疏表示才能够被正确计算。
  对遮挡的鲁棒性。遮挡对于稳健的真实人脸识别造成了相当大的阻碍[16]，[28]，[29]。这个困难主要是由于遮挡所导致的误差存在不可预测的自然性：它可能影响到图像的任何一部分并且可能是任意量级的。然而，这个误差通常只腐蚀图像像素的一小部分，因此在单个像素给出的标准基下是稀疏的。当误差有这样一个稀疏表示时，在我们的框架中，它能够被一致的处理：这些用于误差稀疏表示的基可以被视为是训练样本中一个特殊的类。随后，在这个扩展的字典上（训练样本+误差基）对一个有遮挡的测试图像进行稀疏表示，自然的就把测试样本遮挡部分的成分和测试对象的主体成分分离（如图1）。在这个背景下，稀疏表示和压缩感知理论描述了什么时候这个主体和误差分离可以发生，从而推断出识别算法可以容忍多大面积的遮挡。
  关于这片文章的组织。在第2部分，我们提出了一个基本的通用框架用于基于稀疏表示的分类，这个框架可以应用于基于图像的目标识别的各种各样的问题。我们也将会讨论为什么稀疏表示能够通过$l^1$范数最小化计算，并且稀疏表示怎么样才能被用于对任何给出的测试样本进行分类和验证。第3部分展示了怎么样运用这个通用的分类框架来研究基于图像的人脸识别领域中两个重要的问题：特征提取和对遮挡的鲁棒性。在第4部分，我们在流行的人脸数据集上用大量的实验证明了我们所提出的方法的有效性，并和其他最先进的人脸识别方法进行比较。我们所提出的方法和NN、NS的进一步关系会在增补的附录中所讨论到，相关内容请访问计算机协会数字图书馆：http://doi.ieeecomputersociety.org/10.1109/TPAMI.2008.79。
  虽然所提出的方法对于总体意义上的目标识别有着广泛的前景，但是本文的研究和实验结果仅局限于正面的人脸识别。我们将会处理光照和表情，但是我们并没有明确的考虑到目标姿势或者是依赖人脸的3D模型。再比如，由于配准误差，所提出的算法对于姿势和位移的小变化具有鲁棒性。然而，我们需要假设在应用我们的算法之前，人脸的检测、裁剪和标准化已经预先被执行。

2 基于稀疏表示的分类

  目标识别中的一个基本问题是，用来自 $k$ 个不同类的带有标签的训练样本来正确的判定新的测试样本属于哪一类。我们把给出的来自第 $i$ 类的 $n_i$ 个训练样本表示为矩阵 $A_i\doteq [v_{i,1},v_{i,2},\dots ,v_{i,n_i}]\in {\mathbb{R}}^{m\times n_i}$ 的列。在人脸识别的背景下，我们会将一张 $w\times h$ 的灰阶图像定义为向量 $v\in {\mathbb{R}}^m(m=wh)$ ，这个向量是用图像的各列堆叠出来的;从而 $A_i$ 中的所有列向量表示就是第 $i$ 个目标类的所有训练人脸图像。

2.1 测试样本表示为训练样本的稀疏线性组合

  大量的统计学的模型、生成模型和判别模型被提出，利用 $A_i$ 的结构来进行识别。一个及其简单但是有效的方法就是利用来自单个类的样本在线性子空间上建模。子空间模型对于抓取真实数据集中尽可能多的变量足够灵活，尤其在人脸识别的环境中（在这个环境中，不同光照下和表情的人脸图像位于一个特殊的低维子空间（通常叫做人脸子空间）[24]，[30]）能够被很好的激励。尽管所提出的框架和算法能够引用于多模型或者是非线性分布（在增补的附录中了解更多细节，请访问计算机协会数字图书馆http://doi.ieeecomputersociety.org/10.1109/TPAMI.2008.79），为了使表示更轻松，我们首先应该假设来自于单个类的训练样本确实处于同一个子空间上。这将是我们会在结论中用到的唯一一个关于训练样本的预备知识。
  给出第 $i$ 个目标类足够的训练样本，$A_i\doteq [v_{i,1},v_{i,2},\dots ,v_{i,n_i}]\in {\mathbb{R}}^{m\times n_i}$，任何同样来自第 $i$ 类的新（测试）样本将大致能由处于同一个线性子空间的训练样本线性表示如下：
$$y={\alpha }_{i,1}{v}_{i,1}+{\alpha }_{i,2}{v}_{i,2}+\cdots +{\alpha }_{i,n_i}{v}_{i,n_i},\text{\hspace{1em}(1)}$$
其中 $a_{i,j}$是标量， $a_{i,j}\in \mathbb{R},j=1,2,\cdots n_i$。
  由于测试样本属于哪个样本在初始条件下是未知的，我们为整个训练集定义了一个新的矩阵 $A$ 来表示来自 $k$ 个目标类所有的 $n$ 个训练样本：
$$A\doteq [A_1,A_2,\cdots ,A_K]=[v_{1,1},v_{1,2},\cdots ,v_{k,n_k}].\text{\hspace{1em}(2)}$$
然后y关于所有训练样本的线性表示可以写成：
$$y=A{x}_0\in {\mathbb{R}}^m,\text{\hspace{1em}(3)}$$
其中，$x_0=[0,\cdots ,0,{\alpha }_{i,1},{\alpha }_{i,2},\cdots ,{\alpha }_{i,n_i},0,\cdots ,0{]}^T\in {\mathbb{R}}^n$，向量 $x_0$ 中除了和第 $i$ 类相关的元素是非零元素之外，其他的元素都是0。
  由于测试样本 $y$ 是由向量 $x_0$ 中的元素来识别的，所以我们需要去通过对线性方程组 $y=Ax$ 进行求解，从而得到稀疏表示 $x_0$ 。注意，尽管如此，使用整个训练集来解得 $x$ 还是和使用一个样本的NN以及使用一个类的NS有很大的区别的。之后我们将会论证，我们可以从这样一个全局表示中得到一个更具有判别性的分类器。对于识别用训练集表示的目标和拒绝用训练集表示的但是并不来自于任何类的异常样本，我们也将会解释为什么我们的全局表示的方法要比这些局部表示的方法（NN或者NS）要好。这些优点并非来自于计算量的提升：我们可以看出，算法的复杂度在训练集的大小上仍然保持线性。
  显然，当m>n时，方程组 $y=Ax$ 是超定的，如果该方程组 $y=Ax$ 存在精确解，那么它一定是唯一的。然而，我们将会在第3部分看到，在稳健的人脸识别中，方程组 $y=Ax$ 往往是欠定的，也就是解不唯一。按照惯例，这个问题可以通过选择最小 $l^2$ 范数解来解决：
$$(l^2):\widehat{x_2}=argmin{\Vert x\Vert }_2\text{subject}\text{to}Ax=y.\text{\hspace{1em}(4)}$$
尽管这个优化问题能够被轻松解决（通过A的伪逆），但是 ${\hat{x}}_2$ 并不能很好的用来识别测试样本 $y$。如例1中所示， ${\hat{x}}_2$ 通常是稠密的，有着与很多来自与不同类的训练样本对应的非零元素。为了解决这个问题，我们转而利用了以下的观察：一个有效的测试样本 $y$通常可以被只来自同一类的训练样本充分的表示。只要目标类的数量k足够大，这个表示往往是稀疏的。举个例子，当k=20的时候，解向量 ${\hat{x}}_0$ 中只有5%的元素是非零的。 ${\hat{x}}_0$ 越稀疏，测试样本y属于哪一个类就越容易被准确的判定。
  以上结论促使我们通过解决以下优化问题来寻找 $y=Ax$ 的最稀疏的解：
$$(l^0):\widehat{x_0}=argmin{\Vert x\Vert }_0\text{subject}\text{to}Ax=y.\text{\hspace{1em}(5)}$$
其中 ${\Vert \cdot \Vert }_0$ 表示 $l^0$ 范数，就是向量中非零元素的个数。事实上，如果 $A$ 中的列处于一般的位置， $y=Ax$ 的一些解x中，只要 $x$ 中的非零元素小于m/2， $x$ 就是唯一的稀疏解：即${\hat{x}}_0=x$[33]。然而，求解一个欠定线性方程组从而寻找最稀疏的解是一个NP难问题，即使求大约解[13]也很难：也就是说，在一般情况下，没有比遍历元素的所有子集更高效的方法来寻找 $x$ 最稀疏的解。

2.2 通过 $l^1$ 最小化求稀疏解

  稀疏表示和压缩感知新兴理论[9],[10],[11]最近的发展表明，如果 $x_0$被认为是足够稀疏的，$l^0$ 最小化问题的求解可以等同于以下的 $l^1$ 最小化问题的求解：
$$(l^1):\widehat{x_1}=argmin{\Vert x\Vert }_1\text{subject}\text{to}Ax=y.\text{\hspace{1em}(6)}$$
这个问题可以通过线性编程方法在多项式时间内求解[34]。当解非常稀疏时，甚至会有更高效的解决方法。比如说，homotopy算法求得有t个非零元素的解时，时间复杂度为 $O(t^3+n)$，在训练集大小上是线性的[35]。

2.2.1 几何解释

  图2给出了为什么 $l^1$范数最小化能够求出足够稀疏解的几何解释[36]。$P_{\alpha }$ 表示为半径为 $\alpha$ 的 $l^1$-球（或者是正轴体）：
$$P_{\alpha }\doteq \left\{x:{\Vert x\Vert }_1\le \alpha \right\}\in {\mathbb{R}}^n.\text{\hspace{1em}(7)}$$
在图2中，$l^1$-球 $P_1$ 被映射成多面体 $P\doteq A(P_1)\subset {\mathbb{R}}^m$ , $P$ 是由所有满足$y=Ax$（其中x的 $l^1$ 范数是小于1的）的 $y$ 组成。
  $P_{\alpha }$ 和多面体 $A(P_{\alpha })$ 的几何关系在比例上是不变的。也就是说，如果我们对$P_{\alpha }$进行比例变换，$A(P_{\alpha })$ 也会进行同样的比例变换。在几何意义上，寻找 $l^1$ 范数最小化的解 ${\hat{x}}_1$ 就相当于放大 $l^1$-球 $P_{\alpha }$直到多面体 $A(P_{\alpha })$ 第一次碰到 $y$。此时 $\alpha$ 的值就等于 ${\Vert {\hat{x}}_1\Vert }_1$。
  现在，假设对于$y=A{x}_0$ 存在稀疏解 $x_0$ 。我们希望知道怎样才能通过（6）正确的解得 $x_0$。这个问题通过图2中的几何表示很容易就能够被解决：由于 ${\hat{x}}_1$ 是通过同时放大 $P_{\alpha }$ 和 $A(P_{\alpha })$，直到 $A(p_{\alpha })$ 碰到 $y$ ,故 $l^1$ 最小化的解 ${\hat{x}}_1$一定会在 $P$ 的边界上生成 $A{\hat{x}}_1$。
  因此，如果点 $A(x_0/{\Vert x_0\Vert }_1)$ 在多面体 $P$ 的边界上，那么 ${\hat{x}}_1=x_0$。如图2中举的例子，很容易看出 $l^1$ 最小化解出了所有只有一个非零元素的 $x_0$。这个等式能够成立是因为 $P1$ 的所有顶点都映射在 $P$ 的边界上。
  通常情况下，如果 $A$ 将 $P1$ 所有 $t$ 维平面都映射到 $P$ 上，那么多面体 $P$ 就被称为是（中心）t邻多面体（任意k个顶点均为某个面的顶点集的多面体）[36]。从以上我们可以看出，只有当 $P$ 是 $t$邻多面体时， $l^1$ 最小化（6）才能正确求出所有含有小于等于t+1个非零元素的 $x_0$，在这种情况下，$l^1$ 最小化才等同于 $l^0$ 最小化（5）。这种情况非常常见：即使是由随机矩阵给出的（比如：均匀，高斯和偏傅里叶矩阵）多面体P都是高度相邻的[15]，都能够用 $l^1$ 最小化正确的求解。
  不幸的是，没有一个已知的算法能够有效的计算出给出多面体P的邻度。最好的已知算法是组合（combinatorial），并且当维度m合适时才有效[37]。当m很大时，一个随机选择的多面体的邻度有很大的概率在
$$c\cdot m<t<\lfloor (m+1)/3\rfloor ,\text{\hspace{1em}(8)}$$
之间浮动，其中c是一个很小的正数[9],[36]。不严格的说，只要 $x_0$ 中非零元素的个数远小于维度m的话， $l^1$ 最小化就能够求出 $x_0$。

2.2.2 处理小的稠密噪声

  至此，我们假设等式（3）已经被精确的处理。但是由于真实的数据存在噪声，测试样本不可能由训练样本精确的稀疏表示。模型（3）可以通过加上一个足够小的稠密噪声做出改进，表示如下：
$$y=A{x}_0+z,\text{\hspace{1em}(9)}$$
其中 $z\in {\mathbb{R}}^m$ 是一个有界噪声符号,并且 $\Vert z\Vert <\epsilon$。稀疏解 $x_0$ 仍然可以通过以下稳定的 $l^1$ 最小化近似解出：
$$(l_s^1):{\hat{x}}_1=argmin{\Vert x\Vert }_1\text{subject}\text{to}{\Vert Ax-y\Vert }_2\le \epsilon .\text{\hspace{1em}(10)}$$
  这个凸优化问题可以通过二阶锥编程有效的解决[34]。$(l_s^1)$ 的解一定可以在全体随机矩阵A[38]中近似的求出：$\rho$ 和 $\zeta$ 是常量，有很大的概率认为，如果 ${\Vert x_0\Vert }_0<\rho m$ 并且 ${\Vert z\Vert }_2\le \epsilon$ ,那么计算得到的 ${\hat{x}}_1$ 需要满足：
$$\Vert \widehat{x_1}-x_0\Vert \le \zeta \epsilon .\text{\hspace{1em}(11)}$$

2.3 基于稀疏表示的分类（SRC）

  从训练集的一个类中给出一个新的测试样本 $y$，我们首先通过 (6) 和 (10)来计算 $y$ 的稀疏表示 ${\hat{x}}_1$。理想状况下，所预测的稀疏表示 ${\hat{x}}_1$ 中的非零元素将仅仅和 $A$ 的部分列关联（即这些非零元素是这些列前面的系数），这些列都来自于同一个目标类 $i$，然后我们可以很轻松的把测试样本$y$ 归为这一类。然而，噪声和模型误差可能导致一小部分非零元素与不同目标类关联（如图3）。基于全局的稀疏表示，我们可以设计很多可能的分类器来解决这个问题。比如，我们可以简单的将y归为与 ${\hat{x}}_1$ 中最大元素相关联的目标类中。但是，这种方法并没有利用到与人脸识别中的图像相关的子空间结构。为了更好的利用这样的线性结构，我们通过比较 ${\hat{x}}_1$ 中与哪个目标类中所有训练样本的相关联的元素能够更好的重构y，来对y分类。
  对于每一类 $i$，令 ${\delta }_i:{\mathbb{R}}^n\to {\mathbb{R}}^n$ 为一个描述函数，作用是选择只和第 $i$ 类相关联的系数。对于 $x\in {\mathbb{R}}^n,{\delta }_i(x)\in {\mathbb{R}}^n$是一个新的向量，${\delta }_i(x)$中所有的非零元素是向量 $x$ 中只与目标类 $i$ 相关联的元素。使用只与第 $I$ 类相关联的系数，我们可以大概重构出给出的测试样本 $y$，记为 ${\hat{y}}_i=A{\delta }_i({\hat{x}}_1)$。然后我们就可以根据哪个类能够使得 $y$ 和 ${\hat{y}}_i$ 之间的残差最小，来对 $y$ 进行分类：
$$\underset{i}{\min }{r}_i(y)\doteq \Vert y-A{\delta }_i({\hat{x}}_1){\Vert }_2.\text{\hspace{1em}(12)}$$
以下的算法1概括了完整的识别步骤。我们的执行通过一个基于[39]和[40]，用于线性编程的对偶算法来最小化 $l^1$范数。

例1（$l^1$最小化 vs $l^2$ 最小化）

为了阐述算法1是怎么工作的，我们随机选择了Extended Yale B 数据库中2414张图像的一半作为训练集，剩下的部分用于测试。在这个例子中，我们对所有的图像进行下采样（subsample），使得每一张图片的大小从初始的192 $\times$ 168降到了12 $\times$ 10。下采样图像的所有像素值构成一个120维的特征，堆叠成算法中 $A$ 的列。因此，矩阵 $A$ 的大小为120 $\times$ 1207，并且方程组 $y=Ax$ 是欠定的。图3a展示了一个来自第1类的测试图像通过算法求出的稀疏系数。该图也展示了对于于两个最大系数的特征图像和原始图像。这两个最大的系数都来自于目标类1中的训练样本。图3b展示了38个类的投影系数 ${\delta }_i(x),i=1,2,\dots ,38$ 的残差。使用12 $\times$ 10的下采样图像作为特征，算法1在Extended Yale B 数据库总体来说能够达到92.1%的识别率。（如果需要了解更多细节，算法使用另外一些特征（如：Eigenfaces和Fisherfaces）的表现以及和其他算法的比较，请见第4部分）。鉴欠定方程组 $y=Ax$ 更加传统的最小化 $l^2$ 范数解往往是非常稠密的，最小化 $l^1$范数往往能够找到稀疏解，并且当解是足够稀疏的话，被证明能够找到最稀疏的解。为了阐明最小化 $l^2$ 范数和最小化 $l^1$范数的差异，图4a展示了同样的测试样本的系数，通过传统的 $l^2$ 最小化（4）求出，图4b展示了关于38个目标类的残差。很明显，图4中的系数远远没有由 $l^1$ 最小化求出的系数（见图3）稀疏，并且图4中最主要的系数并不与目标1相关联。因此，图4中残差项最小的类并不是正确的目标类（目标类1）。

2.4基于稀疏表示的验证

  在为给出的测试样本进行分类之前，我们必须确认测试样本是否是一个来自数据集中任意一个类的有效样本。检测然后拒绝无效测试样本（或者是奇异值）的能力对于一个在真实环境下工作的识别系统来说是至关重要的。比如一个人脸识别系统，可能会被给出一个不是数据库中任何一个目标的人脸图像或者一张甚至都不是人脸的图像。
  基于传统分类器比如NN或NS的系统，通常使用残差 $r_i(y)$ 进行检验和识别。也就是说，算法基于最小的残差来接受和拒绝一个测试样本。然而每一项残差 $r_i(y)$ 的计算和训练数据集中的其他目标类没有任何关系，并且仅仅测量了测试样本和每一个单独目标类的相似性。
  在稀疏表示范例中，系数 ${\hat{x}}_1$ 是根据所有类的图像全局计算的。在一定程度上，它能够利用所有类的联合分布来进行验证。我们主张系数 $\hat{x}$ 对于验证来说是一个比残差更好的统计量。让我们通过一个例子来说明。

例2 （稀疏系数的集中）

我们随机的从Google上选择了一个无关的图像并且把它下采样成12 $\times$ 10。然后如例1的那样，在相同的Extended Yale B训练数据中计算这个图像的稀疏表示。图5a画出了得到的系数，图5b画出了相对应的残差。和图3中有效测试图像的系数相比，图5中的系数 $\hat{x}$ 并没有集中在任何一个目标类中，反而广泛的分布在整个训练集当中。因此，估算出来的稀疏系数 $\hat{x}$ 的分布包含了验证测试图像的重要信息：一个有效的测试样本应该有着一个这样的稀疏表示，之中的非零向量大部分都集中在一个目录类中，而无效图像的稀疏表示则广泛的分布在多个目标类中。
  为了量化这个发现，我们通过以下定义来衡量系数在数据集中单个类上的集中度：

定义1（稀疏集中指数（SCI）） 一个稀疏向量 $x\in {\mathbb{R}}^n$ 的SCI被定义如下：
$$\text{SCI}(x)\doteq \frac{k\cdot ma{x}_i\Vert {\delta }_i(x){\Vert }_1/\Vert x{\Vert }_1-1}{k-1}\in [0,1].\text{\hspace{1em}(14)}$$
对于一个通过算法1求得的解 $\hat{x}$ ,如果 $\text{SCI}(\hat{x})=1$，测试样本就仅仅通过只来自一个类的图像表示，如果 $\text{SCI}(\hat{x})=0$，稀疏系数就均匀的分布在所有的类中。我们选择了一个阈值 $\tau \in (0,1)$并且当
$$\text{SCI}(\hat{x})\ge \tau ,\text{\hspace{1em}(15)}$$
时接受测试样本，否则就当做无效样本拒绝。在算法1的第5步中，只有当测试样本通过了这个检验之后我们才能够输出 $y$ 的分类结果。
  不像是NN或者NS，这个新的原则避免了使用残差 $r_i(y)$ 用来分类。注意到在图5中，即使是一个非人脸图像，只要训练集足够大，无效测试样本最小残差也不会太大。相比依赖单个数据量来进行验证和分类，我们的方法把三个任务所需的信息进行了分离：残差用来识别，稀疏表示用来验证。在某种意义上，残差衡量了表示对测试图像的估计有多好，而稀疏集中系数根据局部化衡量了表示本身有多好。
  这个验证方法的一个优点是，在验证一个和很多目标类相似的一般目标时，也有着很好的验证效果。比如，在人脸识别中，一个不属于数据集的普通人脸可能和数据集中的一些目标相当相似，并且关于这些目标类的残差很小。使用残差来验证很有可能导致一个错误的判断。然而，由于一个普通人脸的表示往往需要数据集中大量目标的作用，所以它不可能通过我们的新的验证规则。因此，新的规则能够更好的判定测试样本是一个普通人脸还是数据集中的一个特定目标。在4.7部分，我们会详细说明新的验证规则比NN和NS方法在给出一个无效样本后的验证率要提高10%到20%。（见第4部分的图14或者增补附录中的图18，见计算机协会数字图书馆：http://doi.ieeecomputersociety.org/10.1109/TPAMI.2008.79）

3 两个人脸识别的关键问题

  这一部分，我们研究以上通用的识别框架如何应用到两个人脸识别领域的关键问题上：1）特征变换的选择；2）对于腐蚀、遮挡和伪装的鲁棒性。

3.1 特征提取的作用

  在计算机视觉的文献中，大量的特征提取的方法被研究，以寻找能够在低维空间（通常指人脸空间）更好的分离不同类的投影。一类方法提取全局的人脸特征，如：Eigenfaces [23]、Fisherfaces [24] 和Laplacianfaces [25]。另一类方法试图提取一部分有用的人脸特征（比如眼睛和鼻子周围的一小块） [21]，[41] （一些例子见图6）。传统意义上来说，当特征提取被用于连接像NN和NS这样简单的分类器，特征变换的选择对算法的成功运行来说就很关键。这可能导致一大部分逐渐复杂的特征提取方法的发展，如非线性特征和核特征[42]，[43]。这一部分，我们在新的基于稀疏表示的人脸识别框架中重新检查了特征提取的作用。

  在已经提出的稀疏表示框架之上，特征提取的一个优点是，降低了数据维数和计算代价。对于原始的人脸图像，相关的线性方程组 $y=Ax$ 非常大。举个例子，如果人脸图像以一般的分辨率给出，也就是640 $\times$ 480像素，那么维度 $m$ 可能达到 $10^5$ 数量级。虽然算法1依赖于一些可扩展方法，比如：线性编程，但是将算法1直接用于如此高分辨率的图像上仍然超出了常规计算机的能力。
  由于大部分特征变换都只包括了线性运算（或者接近于线性运算），从图像空间到特征空间的投影可以表示为一个矩阵 $R\in {\mathbb{R}}^{d\times m}$，并且 $d\ll m$。对方程组（3）两边同时使用用 $R$进行投影，得到：
$$\tilde{y}\doteq Ry=RA{x}_0\in {\mathbb{R}}^d\text{\hspace{1em}(16)}$$
实际应用中，特征空间的维度d通常要远小于n。在这种情况下，方程组 $\tilde{y}=RAx\in {\mathbb{R}}^d$是对于未知的 $x\in {\mathbb{R}}^n$ 是欠定的。尽管如此，由于期望解 $x_0$ 是稀疏的，我们可以通过对以下简化的 $l^1$ 最小化问题进行求解从而得到 $x_0$：
$$(l_r^1):{\hat{x}}_1=argmin{\Vert x\Vert }_1\text{subject}\text{to}{\Vert RAx-\tilde{y}\Vert }_2\le \epsilon .\text{\hspace{1em}(17)}$$
其中误差容忍度 $\epsilon >0$。因此，在算法1中，训练图像的矩阵 $A$ 被 $d$ 维特征矩阵 $RA\in {\mathbb{R}}^{d\times n}$ 代替；测试样本 $y$ 被它的特征 $\tilde{y}$所代替。
  对于现存的人脸识别方法，由先前研究的经验发现，只要特征 $R{A}_i$ 没有变得退化，那么维度 $d$ 的增加通常能够提高识别率[42]。由于它几乎不需要 $\tilde{y}$ 在或者接近 $R{A}_i$——即在类判定分析中并不需要依赖协方差 ${\sum }_i=A_i^T{R}^{T}R{A}_i$ 非奇异，所以退化并不是 $l^1$ 最小化中的一个问题。稳定的 $l^1$ 最小化版本（10）或者（17）在统计学文献中被称为Lasso [14]。当期望解稀疏时，它有效的调整高度欠定线性回归，并被证明在一些带噪声的过定环境中是连续的[12]。
  对于我们用于识别的稀疏表示方法，我们将会说明特征提取 $R$ 的选择是怎样影响 $l^1$ 最小化（17）求得正确稀疏解 $x_0$ 的能力的。从 $l^1$最小化的几何解释（见2.2.1部分）来看，以上问题的答案依赖于相关的新轴体 $P=RA(P_1)$ 是否保持足够的邻度。很容易看出，轴体 $P=RA(P_1)$ 的邻度随着 $d$的增加而增加 [11]，[15]。在第4部分，我们的实验结果将会证实 $l^1$ 最小化适用各种特征求得人脸识别稀疏表示的能力，尤其是对于稳定版本（17）。这也意味着大部分人脸识别领域中流行的基于数据的特征（如：eigenfaces和Laplacianfaces）确实能够得到高度邻近的轴体P。
  对高维几何轴体的进一步的分析揭示了一些惊人的发现：如果解 $x_0$ 足够稀疏，并且d是一个足够大的数，那么有极大的概率可以通过 $l^1$ 最小化正确的求出线性方程组 $\tilde{y}=RA{x}_0$的解。更精确来说，如果 $x_0$ 有着 $t$ 个非零元素 $(t\ll n)$，那么只要：
$$d\ge 2tlog(n/d)\text{\hspace{1em}(18)}$$
随机线性衡量就足够让 $l^1$ 最小化求出正确的稀疏解 $x_0$ [44]。这个惊人的发现被称为“维度的祝福”[15]，[46]。随机的特征可以被看做是经典人脸特征（如：Eigenfaces和Fisherfaces）没那么结构化的等同体。据此，我们可以将根据高斯（Gaussian）随机矩阵生成的线性投影称为Randomfaces。

定义2（randomfaces） 考虑到一个变换矩阵 $R\in {\mathbb{R}}^{d\times m}$中的元素是从一个均值为0的正态分布中独立采样的，并且每一行都被标准化为单位长度。$R$ 的行向量可以被看做是 ${\mathbb{R}}^m$ 的 $d$ 张随机人脸。

  一个Randomfaces的主要优点是它们能够很高效的被生成，因为变换 R 是独立于训练数据集的。这个优点对于人脸识别系统来说是非常重要的，因为我们可能并不能获得所有目标类一个完整的数据集来预先计算依赖数据的变换（如:Eigenfaces），或者数据集中的目标可能随时会发生改变。在这种情况下，我们就不需要再次计算随机变换 R。
  只要能够求出正确的稀疏解 $x_0$，不管使用什么样的特征，算法1将会始终给出相同的识别结果。因此，当特征的维数 $d$ 满足以上的限制（18），使用不同特征的算法1都将会快速聚集，并且是否选择一个“最优的”特征变换变得不再至关重要：即使是随机的投影或者是下采样图像都应该和其他精心设计的特征表现得一样好。这一点将会在第4部分的实验结果中被证实。

3.2对于遮挡和腐蚀的鲁棒性

  在很多可行的人脸识别方案中，测试图像 $y$ 可以可能被部分的腐蚀或者遮挡。在这种情况下，上面的线性模型（3）可以被改进为：
$$y=y_0+e_0=A{x}_0+e_0,\text{\hspace{1em}(19)}$$
其中 $e_0\in {\mathbb{R}}^m$ 是一个误差向量——其一小部分（$\rho$）元素为非零向量。$e_0$ 模型中的非零向量是 $y$ 中被腐蚀或者是被遮挡的像素。不同测试图像有着不同的腐蚀位置并且计算机对这些位置是未知的。这些误差可能有着任意量级因此不能够被忽略或者当做2.2.2部分的小噪声来对待。
  编码理论[52]中一个重要的原则是测量结果中的冗余度对于检测和更正过失误差很重要。冗余提高了目标识别的效果，原因是图像像素的数量通常要比形成图像的目标多得多。在这种情况下，即使一小部分像素完全被遮挡，基于剩下像素进行识别仍然是可能实现的。另一方面，在之前部分中讨论的特征提取方法将会去掉那些可能帮助消除遮挡的信息。这种情况下，没有任何一种表示比原始的图像更加冗余、稳健并且能提供更多的有用信息。因此，当处理遮挡和腐蚀时，我们应该使用尽可能高的分辨率，只有当原始图像的分辨率太高以至于不能够处理时，我们才使用下采样或者是特征提取。
  当然，如果冗余没有有效的计算工具来利用冗余数据中的有效编码信息，那么它也就没有用处。直接处理原始腐蚀图像的困难已经导致了研究者们转向利用空间局部性作为稳健识别的一个指导原则。局部特征通过一小部分图像像素进行计算，这些像素上由于遮挡所造成的腐蚀显然要比全局特征少得多。在人脸识别领域，像ICA[53]和LNMF[54]这类方法利用以上的发现来自适应的选择局部集中的过滤器基准。由于局部二值模式（LBP）[55]和Gabor小波[56]都是在局部图像区域上计算的，因此它们有着相似的特性。一个相关的方法把图像分成固定的区域并且分别计算每一个区域的特征[16]，[57]。值得注意的是，局部集中的基上的投影只是转化了遮挡问题的计算域，但并没有消除遮挡。原始像素上的误差变成了转化后的计算域上的误差并且可能变得没有那么具有局部性。由于没有基或者特征要比原始图像像素本身更加具有空间局部性，因而特征提取在利用空间局部性中的作用因此让人质疑。事实上，使得基于空间的方法变得稳健的最流行的办法就是在单个像素上进行随机采样[28]，有时也利用多元切尾法[29]来协助。
  现在，让我们展示怎么样扩展我们提出的稀疏表示分类框架以处理遮挡问题。首先假设被腐蚀的像素是图像中相当小的一部分。误差向量 $e_0$，就像向量 $x_0$ 一样，有着稀疏的非零向量。由于 $y_0=A{x}_0$，我们可以把（19）改进为：
$$y=[A,I]\left[\begin{array}{c}{x}_0\\ e_0\end{array}\right]\doteq B{w}_0.\text{\hspace{1em}(20)}$$
因此，$B=[A,I]\in {\mathbb{R}}^{m\times (n+m)}$，所以方程组 $y=Bw$ 通常是欠定的并且没有唯一的解 $w$。然而，从之前关于 $x_0$ 和 $e_0$ 的稀疏性的讨论，正确的 $w_0=[x_0,e_0]$ 应该最多有 $n_i+\rho m$ 个非零元素。我们因此希望可能求出方程组 $y=Bw$ 最稀疏的解 $w_0$。事实上，对于一般情况下的矩阵B，只要 $y=B\tilde{w}$ 中的 $\tilde{w}$ 有着少于 $m/2$ 的非零元素，那么 $\tilde{w}$ 就是唯一的稀疏解。因此，如果遮挡 $e$ 遮挡了少于 $\frac{m-n_i}{2}$的像素，$\approx$ 图像的50%，稀疏解 $\tilde{w}$ 对于方程组 $y=Bw$ 就是一个有效的值，$w_0=[x_0,e_0]$。
  更一般的情况下，我们可以假设腐蚀误差 $e_0$ 关于一些基 $A_e\in {\mathbb{R}}^{m\times n_e}$ 有着稀疏表示。也就是说，对于一些稀疏向量 $u_0$ 有 $e_0=A_e{u}_0$。在此，我们选择了一些特殊的例子 :假设 $e_0$ 关于自然像素坐标稀疏，则$A_e=I\in {\mathbb{R}}^{m\times m}$。如果误差 $e_0$ 关于其他一些基（比如傅里叶和Haar）更加稀疏，我们可以简单的把矩阵 B 重新定义为在A后面加上 $A_e$ （而不是直接使用 $I$）,因而我们可以转而通过以下等式寻找最稀疏的解$w_0$ ：
$$y=Bw\text{with}B=[A,A_e]\in {\mathbb{R}}^{m\times (n+n_e)}.\text{\hspace{1em}(21)}$$
这样，相同的公式就可以处理更加普遍的腐蚀（稀疏）类。
  像之前那样，我们试着去寻找最稀疏的解 $w_0$ 来解决以下的扩展的 $l^1$最小化问题：
$$(l_e^1):{\hat{w}}_1=argmin{\Vert w\Vert }_1\text{subject}\text{to}Bw=y.\text{\hspace{1em}(22)}$$
也就是在算法1中把图像矩阵 $A$ 换成了扩展的矩阵 $B=[A,I]$ 并且把 $x$ 换成了 $w=[x,e]$。

  显然稀疏解 $w_0$是否能够从以上的 $l^1$最小化中求出依赖于新多面体 $P=B(P_1)=[A,I](P_1)$的邻度。如图7所示，这个新多面体包括了来自训练图像 $A$ 和单位矩阵 $I$ 的顶点。（8）中给出的限制条件意味着如果 $y$ 是一个目标类 $i$ 的图像，那么 $l^1$最小化并不能保证正确的求解出 $w_0=[x_0,e_0]$，除非:
$$n_i+|\text{support}(e_0)|>d/3.$$
通常情况下， $d\ge n_i$，因此（8）意味着在我们希望达到完美重构效果的前提下，最大的遮挡分量为33%。这个限制条件也将会在我们的实验结果中被证明（见图12）。
  为了精确求出多大的遮挡能够被容忍，除了（8），我们需要关于多面体P邻度更多的精确信息。比如，我们想要知道对于一个给出的训练图像，能够处理的最大数量（最坏的可能下）的遮挡是多少。已知用来精确计算一个多面体的邻度的最好算法是自然组合，通过将零空间B和 $l^1$-球交集的搜寻限制在 $l^1$-球的一个随机t面子集上，我们可以得到更紧凑的上限（更多细节见[37]）。我们将使用这个方法来估计所有将在我们实验中用到的训练数据集的邻度。
  根据经验，我们发现稳定的版本（10）只有当我们不考虑模型中的遮挡和腐蚀 $e_0$ 时（比如之前部分所提到的特征提取实例），才有用。当我们通过使用 $B=[A,I]$ 显性的考虑粗差时，使用精确限制 $Bw=y$ 的扩展的 $l^1$ 范数最小化（22）在温和的误差下是稳定的。
  一旦稀疏解 ${\hat{w}}_1=[{\hat{x}}_1,{\hat{e}}_1]$被求出，$y_r\doteq y-{\hat{e}}_1$ 就能够表示一张消除了遮挡和噪声的干净目标图像。为了识别这个目标，我们对算法1中的残差 $r_i(y)$ 进行了如下的轻微改进：
$$r_i(y)\doteq \Vert y_r-A{\delta }_i({\hat{x}}_1){\Vert }_2=\Vert y-{\hat{e}}_1-A{\delta }_i({\hat{x}}_1){\Vert }_2.\text{\hspace{1em}(23)}$$

4 实验验证

  在这一部分，我们在公共数据库上进行了人脸识别实验，以证明所提出的识别算法的有效性和验证之前部分的结论。我们首先将会检查在我们的框架中特征提取的作用，并比较不同种类的特征空间和特征维数的效果，以及比较不同的比较流行的分类器。然后我们将会证明所提出的算法对于腐蚀和遮挡的鲁棒性。最后，我们会证明（使用ROC曲线）稀疏性的作为一个验证测试图像的方法的有效性并且检验怎么样选择训练集能够最大化对遮挡的鲁棒性。

4.1特征提取和识别方法

  我们使用了几个传统的全局人脸特征，即Eigenfaces、Laplacianfaces和Fisherfaces测试了我们的SRC方法并且和两个非传统的特征：Randomfaces和下采样图像比较了它们的效果。我们将我们的算法和3个经典的算法，即之前部分中提到的NN、NS以及线性的SVM进行了比较。在这一部分，我们使用了SRC的稳定版本在各种低维的特征空间上，使用了误差容忍度 $\epsilon =0.05$来解决简单优化问题（17）。算法1的简单（特征空间）版本在经典的3-GHz电脑上通过MATLAB实现，在每个测试图像上只花费了几秒钟。

4.1.1 Extended Yale B 数据库

  Extended Yale B数据库由38个人的2414张正面人脸图像组成。裁剪和标准化后的192 $\times$ 168人脸图像是在各种实验室控制的灯光条件下拍摄的[59]。对于每一个目标，我们随机的选择了一半的图像用于训练（大概每个人32张图像），另一半用于测试。随机选择训练集以保证我们的结果和结论将不会依赖于任何训练数据的特殊选择。
  我们计算了特征空间维度分别为30、56、120、和504时的识别率。这些数字分别对应下采样率为1/32、1/24、1/16和1/8。值得注意的是，由于最大数量的有效Fisherfaces特征数比类数 $k$ （在本例中为38）少1，因此Fisherfaces和其他特征不同。因此，在我们的实验中，只有当维度为30时，Fisherfaces的识别结果才有效。
  NS算法的子空间维度是9，这已经在只有光照变化的人脸图像处理文献中被广泛接受。图8展示了四种不同分类器：SRC、NN、NS和SVM在不同特征下的识别效果。

  对于所有的120维特征空间，SRC的识别率在92.1%和95.6%之间，并且在504维的Randomfaces特征上有着最高的识别率——98.1%。NN、NS以及SVM最大的识别率分别为90.7%、94.1%以及97.7%。所有识别率的表格能够在增补附录中（详见计算机协会数字图书馆 http://doi.ieeecomputersociety.org/10.1109/TPAMI.2008.79
）进行查询。图8中所展示的识别率对于文献中已经被报道出来的方法是连续的，尽管一些报道出来的方法是基于不同的数据库或者是不同的训练集。比如，He 等人[25]提出了在Yale人脸数据库中，当维度为33时使用Eigenfaces的识别率为75%，当维度为28时使用Laplacianfaces的识别效率为89%。在[32]中，Lee等人提出了在Yale B数据库上使用NS方法的精确识别率为95.4%。

4.1.2 AR数据库

  AR数据库由126个人的4000张正面人脸图像组成。对于每一个人，26张图像被分为两部分[60]。这些图像比Extended Yale B数据库包含更多的人脸变量，比如光照变化、表情变化和人脸遮挡。在这个实验中，我们选择了由50个男人和50个女人组成的数据子集。对于每一个对象，只选择了有光照变化和表情变化的14张图像：7张图像作为第一部分用于训练，剩下的7张作为第二部分用于测试。这些图像被裁剪成维度为165 $\times$ 120并且被转化为灰度图像。我们选择了4个特征空间维度：30、54、130以及504，分别对应下采样率为1/24、1/18、1/12和1/6。因为对象的个数为100，Fisherfaces的结果分别在维度为30和54时给出。
  由于目标数变成了100，在这个数据库的实验本质上比Yale数据库上的实验要更具挑战性，但是训练图像被缩减为每个目标7张图像：4张有着不同光照条件的不带表情的脸以及3张不同表情的脸。对于NS，由于每个目标训练样本的数量为7，任何人脸子空间的估计都不能大于7。在本例中，我们选择了保持所有的7维。
  图9展示了该实验的识别率。当使用504维特征时，SRC的识别率在92.0%和94.7%之间。另一方面，NN和NS的最好的识别率分别为89.7%和90.3%。SVM在这个数据集中表现得稍微比SRC要好，最高的识别率达到了95.7%。然而，SVM的效果在选择不同的特征空间时差别很大——使用随机特征时的识别率只有88.8%。增补附录中包含了一个数值结果的表格（详见计算机协会数字图书馆 http://doi.ieeecomputersociety.org/10.1109/TPAMI.2008.79
）。

  基于Extended Yale B数据库和AR数据库的实验结果，我们可以得出以下结论：

1. 在Extended Yale B数据库和AR数据库上，任何特征维度下，SRC和SVM的最好效果都要优于NN和NS这两种经典方法的最好效果。更具体的说，SRC在Yale数据库上的最高识别率为98.1%，SVM为97.7%，NS为94.0%，NN为90.7%；SRC在AR数据库上的最高识别率为94.7%，SVM为95.7%，NS为90.3%，NN为89.7%。
2. 其他三个分类器的效果非常依赖于最优特征的选择——Fisherfaces用于低维空间；Laplacianfaces用于高维空间。NN和SVM中，不同特征的效果并不随着特征空间维度的增加而聚集。
3. 实验结果证明了压缩感知理论：（18）意味着在Yale数据库上，当 $d\approx 128$ 时，随机线性衡量对于求出稀疏解已经足够；在AR数据库上，当 $d\approx 88$ 时，随机线性衡量对于求出稀疏解已经足够[44]。超过这些维度，使用 $l^1$最小化的不同特征的效果就会聚集，传统的特征和非传统的特征（如：Randomfaces和下采样图像）有着相似的表现。当特征维度很大时，单个的随机投影表现最好（Yale数据库上的识别率为98.1%，AR数据库上的识别率为94.7%）。

4.2 局部人脸特征

  在人类和计算机视觉文献中，已经有大量关于验证局部人脸识别的有效性的研究，如[21]和[41]。作为实验的第二部分，我们在三个局部人脸特征上测试了我们的算法：鼻子、右眼和包含嘴巴和下巴的部分。我们在Extended Yale B数据库上使用了和4.1.1部分相同的测试集进行了实验。从图10中可以看到一个典型的特征提取的例子。

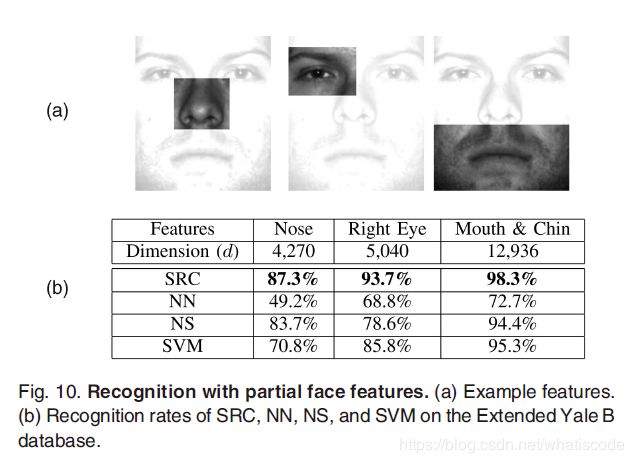
  对于三个特征中的任意一个特征，维度 $d$ 要比训练样本的数量要大（n=1207），因而需要求解的线性方程组（16）变成了过定的。然而，稀疏近似解 $x$ 仍然能够通过解决 $\epsilon$-相关的 $l^1$ 最小化问题（17）得到（在此， $\epsilon =0.05$）。图10的结果再一次正确的证明了所提出的SRC算法的识别率比NN、NS和SVM更高。这些实验也证明了所提出的算法在超过 $10^4$ 维特征上的可扩展性。

4.3 在随机像素腐蚀上的识别

  对于这个实验，我们在Extended Yale B数据库上测试了SRC的稳定版本，这个稳定版本解决了扩展的 $l^1$ 最小化问题（22）。我们使用子集1和子集2（717张图像，正常到适度的光照条件）用于训练，子集3（453张图像，极端的光照条件）用于测试。在没有遮挡的情况下，这是一个相当容易的识别问题。为了隔离出遮挡的作用，选择必须经过谨慎考虑。图像被裁剪为96$\times$ 84，因此在这个例子中，$B=[A,I]$是一个8064 $\times$ 8761的矩阵。对于这个数据集，我们估计多面体 $P=conv(\pm B)$ 的邻度大约为1185（使用[37]中给出的方法），意味着最大13.3%的遮挡可以被完美的重构。
  我们从每一个测试样本中随机选择了一部分像素进行腐蚀，把这些像素的值换成了均匀分布中的独立同分布样本。腐蚀的像素是从每一个测试样本中随机选择的，因此这些像素的位置对于算法是未知的。我们腐蚀像素的比例从0%到90%。图11a、11b、11c和11d展示了一些测试图像的样本。当超过50%的腐蚀比例，腐蚀的人脸图像就已经不能够被人眼所识别（如图11a的第二幅和第三幅图像），识别它们似乎就成为了不可能的问题。然而，即使是在这种极端情况下，SRC仍然能够正确的识别目标。

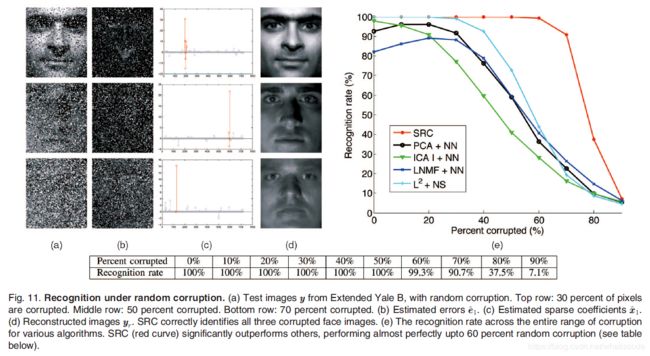
  我们定量的将我们的方法和视觉文献中的其他4种人脸识别方法进行了比较。[23]中的主成分分析法（PCA）对于遮挡并没有鲁棒性。有很多改进使得PCA对于腐蚀或者是不完整数据具有了鲁棒性，并且有的改进已经被应用到了稳健的人脸识别，如[29]。我们稍后将会讨论我们的算法在实际应用条件下的效果。在此，我们使用基本的PCA来提供一个比较的标准。剩下的3中方法则对于遮挡更具有鲁棒性。独立成分分析（ICA）构架 I [53]试图去用一个统计学的独立基图像的线性组合来表示训练集。局部非负矩阵分解（LNMF）使用基图像的加法组合来近似表示训练集，并偏向于使用稀疏基进行运算。最后，为了说明所提高的鲁棒性确实是来自于 $l^1$ 范数的使用，我们和最小二乘法（首先把测试样本投影到由所有人脸图像构成的子空间，然后再执行NS）进行了比较。图11e给出了SRC和它的4个竞争者的识别效果在不同腐蚀程度下的函数图。我们发现SRC比其他4中算法表现得都要好。从0到50%的遮挡率，SRC正确识别了所有的目标。在50%的腐蚀下，其他的算法中没有一个算法的识别率是高于73%的，而SRC的识别率是100%。甚至在70%的遮挡下，SRC的识别率仍然能够达到90.7%。这远远超过了理论上最差情况下算法能够容忍的腐蚀值——13.3%。显然，最差情况下的分析对于随机腐蚀过于保守。

4.4 在随机遮挡块上的识别

  我们接下来模拟不同程度的邻近遮挡，从0到50%，通过将每个测试样本中随机位置的方块换成一个不相关的图像，如图12a所示。相类似的，遮挡的位置随机选择因此对于计算机是未知的。选择人脸特征或者是图像块的方法（如[16]和[57]），由于遮挡位置的不可预测性变得没有那么有效。图12a、12b、12c和12d的前两行展示了算法1在30%遮挡下的两个表示结果。图12a是遮挡图像。在第二行中，人脸的整个中心部分都被遮挡；这对于人类都是一个很难完成的识别任务。图12b展示了估计误差 ${\hat{e}}_1$ 的量级。值得注意的是， ${\hat{e}}_1$ 不仅由狒狒图像的遮挡构成，还包含了由于噪声阴影所造成的线性子空间模型的异常。图12c画出了系数向量 ${\hat{x}}_1$ 的预测值。红色的元素是对应于正确测试样本的的系数。在所有的例子中，所估计的系数是稀疏的并且对于同一个人的测试图像有着很大的量级。在所有例子中，SRC算法正确的识别了遮挡图像。对于整个数据集，在PowerMac G5电脑通过MATLAB进行的实验对于每个测试图像需要90秒的测试时间。

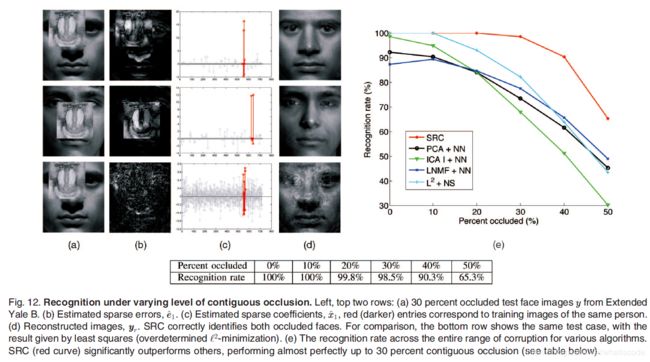
  图12e中的函数图展示了所有5个算法的识别率。SRC再一次比其他4个算法在所有不同遮挡程度上都要表现得好。在30%的遮挡上，算法1表现得几乎完美，正确识别了98%的测试目标。即使是在40%的遮挡上，只有9.7%的目标未能够识别成功。与随机像素的腐蚀相比，相邻的遮挡对于算法肯定是一种更坏的误差。尽管如此，要注意的是，我们的算法并没有假设有任何的自然腐蚀或遮挡的先验知识。在4.6部分，我们将会看到邻近遮挡的先验知识是如何被用于改进算法并且显著提高识别效果的。
  这个实验结果对于在人脸识别中应该使用全局特征还是局部特征的讨论[22]有着有趣的影响。由于他们的基是局部集中的，遮挡只腐蚀了一小部分系数，所以这意味着ICA和LNMF对于遮挡都具有鲁棒性。相反，如果使用 $l^2$ 最小化（垂直投影）来根据像训练样本本身的全局基表示遮挡图像，那么所有的系数都可能被腐蚀（如图12第3行）。这个后果所来带来的问题将会是表示怎样被计算，而不是选择全局还是局部基表示测试样本。合适的利用冗余和稀疏性是误差更正和鲁棒性的关键。提取局部或者是不相交的特征只能降低冗余，从而导致更弱的鲁棒性。

4.5 在伪装上的识别

  我们使用了AR人脸数据库上的一个数据集测试了SRC处理现实中故意遮挡的能力。被选择的数据集包含了100个目标（50名男性，50名女性）的1399张图像（除了一张腐蚀图像 w-027-14.bmp之外，每个目标14张）。我们使用了799张（大概每个目标8张）有着不同表情的无遮挡正面人脸图像用于训练，通过一个大小为4980 $\times$ 5779 的矩阵B表示。我们估计多面体 $P=conv(\pm B)$ 的邻度大约为577，也就意味着最多在11.6%的遮挡下能够很好的重构。在PowerMac G5电脑通过MATLAB进行的实验对于每个测试图像需要75秒的测试时间。
  我们把200张测试图像分成了两个测试集。第一个测试集包含了带墨镜的目标图像，墨镜大概遮挡了图像20%。图1a展示了这个测试集中的一个成功实例。注意到对于由墨镜所导致的遮挡， ${\hat{e}}_1$由图像边缘很小的误差构成。第二个测试集包含了带着围巾的目标图像，围巾大概遮挡了图像的40%。由于这个遮挡率大概是能够由邻度 $conv(\pm B)$ 所给出的最坏情况下最大遮挡率的3倍，我们的算法可能在这个范围内并不能成功。图13a展示了一个失败的案例。图中最大的系数对应的胡须男的图像中，他的嘴巴部分和围巾相似。

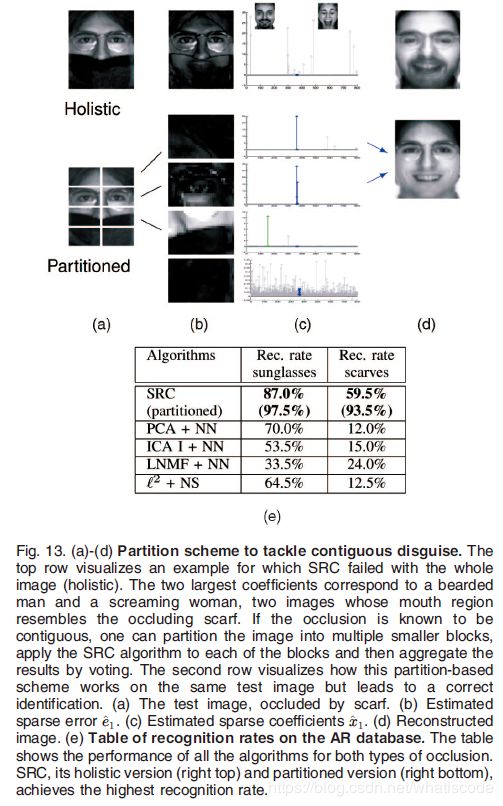
  图13e的表格对SRC和其他4种之前部分描述过的算法进行了对比。在被墨镜遮挡的人脸图像上，SRC达到了87%的识别率，比第二高的竞争者多出了17%。对于被围巾遮挡的人脸图像，识别率为59.5%，比第二高的竞争者的两倍还要多。尽管这个实验结果证实了，当遮挡率超过了训练集的邻度所确定的最大值时，算法对于随机遮挡仍具有鲁棒性，但是一旦超过了这个最大值，来自不同的训练样本相似局域的遮挡可能会导致算法的识别失败。因为一旦遮挡的量超过了这个临界值，额外的假设，比如伪装都是连续的，则需要达到更好的识别效果。

4.6 通过分块来提高识别效果

  到目前为止，我们还没有利用很多现实识别方案中存在的事实：即一些块状的图像像素的遮挡虽然不知道具体的位置，但是他们确实是连在一起的。一个比较传统的方法（在[57]和其他文献中发现）通过把图像分成块状并独立的处理每一块来利用以上的信息。每个独立块的结果都是聚集的，比如：通过投票，丢弃那些被确认为遮挡的块（即使用2.4部分的异常值拒绝规则）。这个方法的主要困难是，遮挡不太可能存在于某些固定的块中；只有一些块会被完全的遮挡，剩下的一部分或者是全部可能会被部分的遮挡。因此，在这样的机制下，仍需要一个稳健的方法来处理每一块。
  我们把每一个训练图像分成了L块，每一块的大小为 $a\times b$ ，从而产生了一个矩阵集 $A^{(1)}\dots ,A^{(L)}\in {\mathbb{R}}^{p\times m}$，其中 $p=ab$。我们相似的把测试样本 $y$ 分成 $y^{(1)},\dots ,y^{(L)}\in {\mathbb{R}}^p$ ，我们把 $l$ 个测试样本写成训练样本 $l$ 个块的稀疏线性组合$A^{(l)}{x}^{(l)}$，再加上稀疏误差 $e^{(l)}\in {\mathbb{R}}^p$：$y^{(l)}=A^{(l)}{x}^{(l)}+e^{(l)}$。我们能够通过 $l^1$最小化求解稀疏 $w^{(l)}=[x^{(l)}{e}^{(l)}]\in {\mathbb{R}}^{n+p}$:
$${\hat{w}}_1^{(l)}\doteq arg\underset{w\in {\mathbb{R}}^{n+p}}{\min }\Vert w{\Vert }_1\text{subject}\text{to}[A^{(l)}I]w=y^{(l)}.\text{\hspace{1em}(24)}$$
我们把这个来自于算法1的分类器应用于每一个块中，并且通过投票使得结果聚集。图13展示了这一个方法。
  我们在AR数据库使用墨镜和围巾伪装的人脸数据证实了这个方法的有效性。我们把每张图像分为8块（4 $\times$ 2），每一块图像的大小为20 $\times$ 30像素。分块将围巾遮挡的识别率从59.5%提高到了93.5%，并且也将墨镜遮挡的识别率从87.0%提高到了97.5%。这个效果超出了AR数据集已知的最好结果（这个工作在50个目标上使用更加复杂的随机采样技术，墨镜遮挡的识别率为84%，围巾遮挡的识别率为93%）。同样值得注意的是[16]，它致力于从每个目标的单个训练样本识别遮挡图像。在AR数据库上，这个方法的识别率达到了80%。
  

4.7 拒绝无效测试图像

  我们接下来将会说明稀疏性与拒绝无效（带遮挡或者无遮挡的）测试样本的相关性。我们在Extended Yale B数据库上根据稀疏集中指数（SCI）（14）测试了奇异拒绝规则（15），像之前那样，我们使用子集1和2来训练，用子集3来测试。我们再一次通过用一个不相关的图像置换测试样本的随机选择的块，模拟了不同程度的遮挡（10%，30%和50%）。然而，在这个实验中，我们仅仅包括了训练集的一半目标。因此，训练集的另一半的目标对于算法来说是新的。我们通过在[0,1]范围内变化阈值 $\tau$，并生成如图14所示的受试者工作特征（ROC）曲线，来测试系统判断一个给出的测试目标是否是训练集的新目标的能力。我们也通过在PCA、ICA和LNMF特征空间中为测试图像（的特征）与最邻近训练图像（的特征）的欧几里得距离设置了阈值，以考虑异常值拒绝项。这些曲线同样也在图14中展示。值得注意的是简单的拒绝规则（15）在10%到30%的遮挡上表现得近乎完美。在50%的遮挡上，它的表现显著的要比其他3个算法要好，并且是4个算法中唯一一个比预期要好的算法。增补附录中包含了更多在AR数据库上使用Eigenfaces的验证结果，再一次说明了ROC的显著改进。

4.8 设计训练样本以达到鲁棒性

  设计识别系统的一个重要考虑就是选择训练样本的数目以及拍摄的条件（光照、表情、视角等等）。训练图像应该要足够大以能够包含所有可能发生在测试集中的条件：从模式识别的观点来说，它们应该是充分的。举个例子，Lee等人[59]阐述了怎么样选择最小的表示图像来大约解释每一个人脸的圆锥。在第2部分所讨论的邻度的概念为怎样才算是一个鲁棒的训练集提供了一个不同的衡量方式：算法所能够容忍的最大数量的遮挡比例直接通过相对应的多面体的邻度确定。由于遮挡目标可能和例外一个训练类的图像非常相似，所以视觉识别中最差的情况是有意义的。然而，如果遮挡是随机的并和训练图像无关（就像4.3部分），算法的平均效果也可能会有意义。
  事实上，这两个重要的概念，充分性和鲁棒性是互补的。图15a展示了在Extended Yale B数据库上四个子集的邻度估计值。注意到子集4（最极端的光照条件）有着最高的邻度，大约为1330。图15b展示了AR数据库上有着不同面部表情的子集的临界点。数据集包含了如图15b所示的四种面部表情：无表情、开心、生气和尖叫。我们从各种表情图像中生成了训练集，并计算了每个训练集相对应的多面体邻度。最具鲁棒性的训练集是分别为无表情+开心的组合，接下来是开心+尖叫的组合；鲁棒性最差的是无表情+生气的组合。值得注意的是，无表情图像和生气图像表现得非常相似，而开心和尖叫非常不相似。

  因此，对于不同的光照（图15a）和不同的表情（图15b），在图像中有着更多变量的训练集对遮挡有着更好的鲁棒性。设计一个允许在各种广泛的条件下识别的训练集并不会限制我们的算法，反而会帮助提高算法的效果。然而，训练集不应该包含太多相似的图像，就像在图15b的无表情+生气的例子。在信号表示的术语中，训练图像应该被称为不相关字典（incoherent dictionary）[9]。

5 结论和讨论

  在这篇论文中，我们通过理论分析和实验验证说明了稀疏性的利用对如人脸图像的高维数据进行高效的分类至关重要。当稀疏性被合理的利用时，特征的选择就没有使用的特征数目重要（在我们的人脸识别例子中，大约100就足够让这些不同特征的差异变得微不足道）。除此之外，遮挡和腐蚀在相同的识别框架中能够被一致并且稳健的处理。在没有特殊工程处理的情况下，通过一个简单的算法就能够对一些遮挡或者腐蚀的图像有着显著的识别效果。
  关于未来工作的一个有趣的问题是，这个框架除了识别之外，是否能够用于目标检测。稀疏性在检测的用处已经在文献[61]和最新发表的[62]中得到了注意。我们相信稀疏性在稳健的目标检测和识别中所有潜在的可能性还没有被完全发掘。从一个实际应用的立场来说，把这个算法应用到限制更少的条件中可能会有用，尤其是不同的目标姿势。对于遮挡的鲁棒性允许算法容忍小的姿势变化和误差。在增补附录中（详见计算机协会数字图书馆 http://doi.ieeecomputersociety.org/10.1109/TPAMI.2008.79）
我们进一步讨论了我们的算法在适应非线性训练分布的能力。然而，在不同姿势下直接表示人脸图像分布所需的训练样本的数量可能过大。在姿势中使用外推法（比如仅仅使用正面训练图像），将会需要整合特征来匹配方法或者是非线性变形模型来用于测试样本的稀疏表示计算。原则上，想要实现以上的方法，仍然需要对未来工作的重要导向。