深入浅出解释FFT（三）——去掉频谱中的直流分量

不论是FFT还是DCT或者其它变换中，都存在将直流分量置零的方法。比如将信号的一阶导数进行FFT变换后置零直流分量。

在模拟部分的电路中，不少元件（如放大器）输出会有直流漂移（即输出应该为零时，实际上是一个直流电压）。这个漂移会对下一级的放大等功能发生影响。所以通常在各级之间采用交流耦合（最简单的就是用一个电容隔开）。这样，信号的直流部分也就不能通过。所以在接收端，所有的直流分量都来自于系统的直流漂移，需要除掉。

另一种情况是模拟电路之间需要阻抗匹配时（如音频放大器和扬声器之间），最简单的方法是用变压器耦合。这时直流也不能通过。

信号处理中的另一种情况是需要提取寄生在很大直流信号上的一个很小的交变信号。这时候也需要去除直流信号。最简便的办法就是傅立叶变换后把直流分量置零。

如果使用直流分量，
1. 和直流偏置混在一起
2. 耗电
3. 浪费DA/AD的动态范围

经常会听说信号做频谱变换后要做去除直流分量的处理，我想请教其理论和具体实现。请大家不吝赐教。

我这里有一个例子，在一正弦信号和一线性信号中加入直流成分。做频谱变换，得到的结果从图上看也确实存在直流成分的干扰，确实需要去除。但我这里是事先已知直流成分。更一般的情况是，对于信号，我们根本不确定是否有直流成分，或者不知道直流成分为多少，对之进行采集，做频谱变换。那么，我们该怎样对频谱做处理，才能消除其中由被采集信号的直流成分导致的误差呢？

我的程序是：

clear,clc

close all

x = 0:1/1024:1-1/1024;

y = sin(2*pi*10*x);

z = fft(y);

figure

stem(-512:511,abs(fftshift(z))/1024);

y = y+ 0.1;

z2 = fft(y);

figure

stem(-512:511,abs(fftshift(z2))/1024);

a=0:1023;

b=fft(a);

figure

stem(-512:511,abs(fftshift(b))/1024);

a = a+50;

b2=fft(a);

figure

stem(-512:511,abs(fftshift(b2))/1024);

a=2.*[0:1023];

a = a+50;

b3=fft(a);

figure

stem(-512:511,abs(fftshift(b3))/1024);

图像就不附在这里了。

观察图像，可以看到，对一正弦信号加了直流分量，变换后直流成分只影响0频，（并且大小刚好是0.1，这是什么意思呢？）此时将0频的信号去掉即可得到准确的频谱。那么，是对所有信号都可以这样处理么？直接将变换后0频幅值变为0，就去掉了直流成分的影响？

——但这对于线性信号显然不行。

对于线性信号，无论是频率为多少，变换结果都是在0频上有值，且加直流成分后值会变大。这里我又有两个问题：

1、为什么我设置的频率明明为1或2，也就是斜率为1或2，变换的频率主峰值却是0？

2、不加直流成分时，0频值代表什么？均值？还是有效值？还是其他？

1  通常数字信号去直流直接减去个均值就可以了，matlab去直流加线性趋势项的函数为detrend，频率1或2和斜率1或2是不等价的，0频可以认为是直流

2  为什么是0.1，傅立叶变换的公式，代入频率为0，看一下就知道了。这也是为什么去均值可以作为去直流的一个手段。当然取决于你的直流分量怎么定义，去均值这个只能去平稳信号的直流分量，象你的线性信号，它不是一个平稳信号，所以很多你看到的结论都是不适用的，从你的结果来看，你要看线性信号的频谱，不严格地想一下，你的线性信号根本没有周期性，也就是所周期是无穷远，所以所有的信号都可以认为是直流分量

3   含直流成分的正弦信号，只有整周期采样时才能在傅里叶变换时得到0频分量刚好是直流分量吧，因为0频分量即是所有信号点求和，整周期正弦信号求和为0，相当于将所有项的直流成分求和，若再除以点数，即是每一点的直流分量。同理，将信号点减去均值的方法，最好也是当信号是整周期采样时才准确吧？比如如果采一个半周期的信号，得到的均值就不是直流分量了。
我的直流分量就是频率为0的信号，在线性信号中，您说去均值不适用，那么该怎么去除影响呢？我理解我的线性信号周期就是1024啊，0增长到1023，然后又开始重复，如此循环。可以不？

4  谢谢解答哦。通常是那样处理的，detrend函数也见过。斜率和频率确实不是一回事，搞混啦。但是我觉得斜率为1的信号其频率不该是0啊，不该出现在0频上，而现在，0频为何有那么大的幅值？也就是说，不加直流成分的线性信号应该在0频没有值才对呀。而且，实际上，0频幅值代表的是信号均值，这是为什么呢？
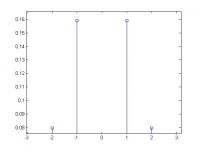
将所有信号点减去均值，再做变换，确实没有0频分量，但是变换结果就不知道啥意思了：
a = 0:1/1024:1-1/1024;
a = a-mean(a);
b=fft(a);
figure
stem(-512:511,abs(fftshift(b))/1024);

5  你这种的线性趋势相当于y=Kx+0.5，所以你的直流为0.5，减去均值后就没有了，所谓线性趋势一般都缓变趋势项，自然是含有很多低频信息了，如果你对信号做傅里叶变换。应该是像sa函数和余弦的混合（我好像看过，但自己没做过）。那是加窗，你的信号有限长，所以相当于你的信号频谱和sinc卷积

6  最开始应该理解不对，忘记了连续和离散的差别，信号的频率和斜率没有直接关系，但是你这种的离散线性趋势和你数据的长度有直接关系，例如你的数据长度是1s，那自然你的1hz处频率最大，数据2s，频率就会0.5最大，而这个信号不是正弦，所以肯定存在其他分量。斜率不同其实就是导致数值不同，可以认为是幅度不同，但形状是相同的，其实这取决于FFT，因为FFT是周期延拓的，而很显然对于直流线性趋势的周期就是数据的长度，注意这和正弦信号有大大的不同。其实之前版主说的也应该就是这个意思。