Matlab 之灰色预测模型GM(1,1)和GM(1,n)

1.灰色系统的定义：
灰色系统指既含有已知信息又含有未知信息的系统。
2.灰色预测模型的定义：
对灰色系统进行预测的模型。
灰色模型（Grey Model，简称GM模型）一般表达方式为GM（n,x）模型，其含义是：用n阶微分方程对x个变量建立模型。
3.灰色预测模型的目的：
通过把分散在时间轴上的离散数据看成一组连续变化的序列，采用累加和累减的方式，将灰色系统中的未知因素弱化，强化已知因素的影响程度，最后构建一个以时间为变量的连续微分方程，通过数学方法确定方程中的参数，从而实现预测目的。
4.灰色系统预测模型的特点：
无需大量数据样本，短期预测效果好，运算过程简单。
5.灰色系统预测模型的不足：
对非线性数据样本预测效果差。

常用的灰色系统预测模型主要有GM(1,1)和GM(1,n)，以下分别对这两种模型展开。
【1】.GM(1,1)模型及其matlab实现
1. GM（1,1）模型的预测原理是：对某一数据序列用累加的方式生成一组趋势明显的新数据序列，按照新的数据序列的增长趋势建立模型进行预测，然后再用累减的方法进行逆向计算，恢复原始数据序列，进而得到预测结果。
2. GM(1,1)建模过程：
(1) 设一组原始数据为，n为数据个数。对累加以便弱化随机序列的波动性和随机性,得到新的数列为：其中，
(2) 生成的邻均值等权数列 其中，
(3) 根据灰色理论对 建立关于t的白化形式的一阶一元微分方程GM(1,1):

其中，a，u为待解系数,分别称为发展系数和灰色作用量，a的有效区间是(-2,2)，并记a，u构成的矩阵为灰参数 ,只要求出参数a，u，就能求出,进而求出的预测值。
(4) 对累加生成数据做均值生成B与常数项向量 :

(5) 用最小二乘法求解灰参数,则
(6) 将灰参数代入，并对 进行求解，得

(7) 将上述结果累减还原，即可得到预测值
(8) 利用模型进行预测:
(9) 对建立的灰色模型进行精度检验,
(9.1)残差检验：
残差：
相对误差：
(9.2)后验差检验：
均值：
方差：
残差的均值：
残差的方差：
后验差比值：
小误差概率：
(9.3) 预测精度等级对照如下：
预测精度等级
好 P>0.95 C<0.35
合格 P>0.80 C<0.45
勉强合格 P>0.70 C<0.50
不合格 P<=0.70 C>=0.65

基于Matlab实现GM(1,1)模型程序：

clear
syms a u;
c=[a,u]';%构成矩阵
A=[15 16.1 17.3 18.4 18.7 19.6 19.9 21.3 22.5];%输入数据，可以修改
Ago=cumsum(A);%原始数据一次累加,得到1-AGO序列xi(1)。
n=length(A);%原始数据个数
for k=1:(n-1)
    Z(k)=(Ago(k)+Ago(k+1))/2; %Z(i)为xi(1)的紧邻均值生成序列
end
Yn =A;%Yn为常数项向量
Yn(1)=[]; %从第二个数开始，即x(2),x(3)...
Yn=Yn';
E=[-Z;ones(1,n-1)]';%累加生成数据做均值
c=(E'*E)\(E'*Yn);%利用公式求出a，u
c= c';
a=c(1);%得到a的值
u=c(2);%得到u的值
F=[];
F(1)=A(1);
for k=2:(n)
    F(k)=(A(1)-u/a)/exp(a*(k-1))+u/a;%求出GM(1,1)模型公式
end
G=[];
G(1)=A(1);
for k=2:(n)
    G(k)=F(k)-F(k-1);%两者做差还原原序列，得到预测数据
end
t1=1:n;
t2=1:n;
plot(t1,A,'bo--');
hold on;
plot(t2,G,'r*-'); 
title('预测结果');
legend('真实值','预测值');
%后验差检验
e=A-G;
q=e/A;%相对误差
s1=var(A);
s2=var(e);
c=s2/s1;%方差比
len=length(e);
p=0;  %小误差概率
for i=1:len
    if(abs(e(i))<0.6745*s1)
        p=p+1;
    end
end
p=p/len;

   
   
   
   

    
    
    
    
1
    
    
    
    
2
    
    
    
    
3
    
    
    
    
4
    
    
    
    
5
    
    
    
    
6
    
    
    
    
7
    
    
    
    
8
    
    
    
    
9
    
    
    
    
10
    
    
    
    
11
    
    
    
    
12
    
    
    
    
13
    
    
    
    
14
    
    
    
    
15
    
    
    
    
16
    
    
    
    
17
    
    
    
    
18
    
    
    
    
19
    
    
    
    
20
    
    
    
    
21
    
    
    
    
22
    
    
    
    
23
    
    
    
    
24
    
    
    
    
25
    
    
    
    
26
    
    
    
    
27
    
    
    
    
28
    
    
    
    
29
    
    
    
    
30
    
    
    
    
31
    
    
    
    
32
    
    
    
    
33
    
    
    
    
34
    
    
    
    
35
    
    
    
    
36
    
    
    
    
37
    
    
    
    
38
    
    
    
    
39
    
    
    
    
40
    
    
    
    
41
    
    
    
    
42
    
    
    
    
43
    
    
    
    
44
    
    
    
    
45
    
    
    
    
46
    
    
    
    
47
    
    
    
    
48
    
    
    
    
49
   
   
   
   

运行结果如下：



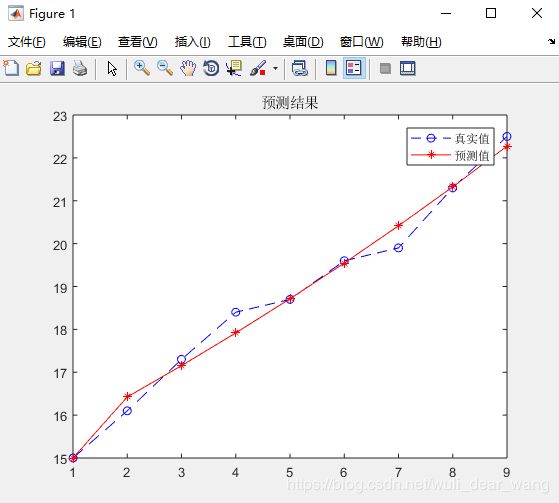
p=1；c=0.0148；预测等级为：好

从运行结果看，对于线性的数据使用GM(1,1)预测，其拟合效果还是不错。

【2】GM(1,n)模型及Matlab实现
1.GM（1,n）模型的预测原理：与GM(1,1)类似，不同在于输入数据变量是n个。
2. GM(1,n)模型的建模过程：
设系统有特征数据序列：
相关因素序列：

(1) 令的1-AGO序列为，其中

(2) 生成紧邻均值序列，其中

称为GM(1,n)模型。
在GM(1,n)模型中，a被称为发展系数，称为驱动系数，称为驱动项。
令 和
再令，由最小二乘参数估计可得，当近似时间相应式为：
累减还原式为
差分模拟式为

基于Matlab实现GM(1,n)预测模型的程序：

A=[560823,542386,604834,591248,583031,640636,575688,689637,570790,519574,614677];
x0=[104,101.8,105.8,111.5,115.97,120.03,113.3,116.4,105.1,83.4,73.3;
    135.6,140.2,140.1,146.9,144,143,133.3,135.7,125.8,98.5,99.8;
    131.6,135.5,142.6,143.2,142.2,138.4,138.4,135,122.5,87.2,96.5;
    54.2,54.9,54.8,56.3,54.5,54.6,54.9,54.8,49.3,41.5,48.9];
[n,m]=size(x0);
AGO=cumsum(A);
T=1;
x1=zeros(n,m+T);

for k=1:(m-1)
    Z(k)=(AGO(k)+AGO(k+1))/2; %Z(i)为xi(1)的紧邻均值生成序列
end
for i=1:n
    for j=1:m
        for k=1:j
            x1(i,j)=x1(i,j)+x0(i,k);%原始数据一次累加,得到xi(1)
        end
    end
end
x11=x1(:,1:m);
X=x1(:,2:m)';%截取矩阵
Yn =A;%Yn为常数项向量
Yn(1)=[]; %从第二个数开始，即x(2),x(3)...
Yn=Yn';
%Yn=A(:,2:m)';
B=[-Z',X];
C=((B'*B)\(B'*Yn))';%由公式建立GM(1,n)模型
a=C(1);
b=C(:,2:n+1);
F=[];
F(1)=A(1);
u=zeros(1,m);
for i=1:m
    for j=1:n
        u(i)=u(i)+(b(j)*x11(j,i));
    end
end
for k=2:m
    F(k)=(A(1)-u(k-1)/a)/exp(a*(k-1))+u(k-1)/a;
end
G=[];
G(1)=A(1);
for k=2:m
    G(k)=F(k)-F(k-1);%两者做差还原原序列，得到预测数据
end
t1=1:m;
t2=1:m;
plot(t1,A,'bo--');
hold on;
plot(t2,G,'r*-'); 
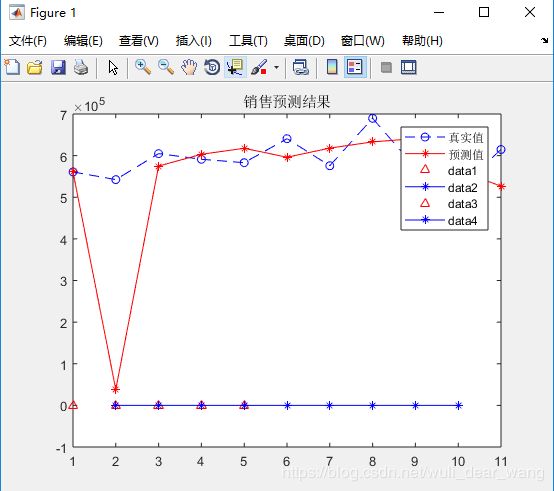
title('销售预测结果');
legend('真实值','预测值');
   
   
   
   

    
    
    
    
1
    
    
    
    
2
    
    
    
    
3
    
    
    
    
4
    
    
    
    
5
    
    
    
    
6
    
    
    
    
7
    
    
    
    
8
    
    
    
    
9
    
    
    
    
10
    
    
    
    
11
    
    
    
    
12
    
    
    
    
13
    
    
    
    
14
    
    
    
    
15
    
    
    
    
16
    
    
    
    
17
    
    
    
    
18
    
    
    
    
19
    
    
    
    
20
    
    
    
    
21
    
    
    
    
22
    
    
    
    
23
    
    
    
    
24
    
    
    
    
25
    
    
    
    
26
    
    
    
    
27
    
    
    
    
28
    
    
    
    
29
    
    
    
    
30
    
    
    
    
31
    
    
    
    
32
    
    
    
    
33
    
    
    
    
34
    
    
    
    
35
    
    
    
    
36
    
    
    
    
37
    
    
    
    
38
    
    
    
    
39
    
    
    
    
40
    
    
    
    
41
    
    
    
    
42
    
    
    
    
43
    
    
    
    
44
    
    
    
    
45
    
    
    
    
46
    
    
    
    
47
    
    
    
    
48
    
    
    
    
49
    
    
    
    
50
    
    
    
    
51
    
    
    
    
52
    
    
    
    
53
   
   
   
   

运行结果如下：

GM(1,1)模型精度检验