GNSS中多频观测值的组合形式
以GPS为例,L1、L2、L5三个频点,为1575.42,1227.60,1176.45MHZ;对应波长为:
1 光速=299792458 米/秒(米每秒)
基频:10.23MHZ; L1为154倍基频, L2为120倍基频, L3为115倍基频,
λ1=c/L1= 0.190293672798365≈19厘米;
λ2=c/L2= 0.244210213424568≈24.4厘米;
λ5=c/L5= 0.254828048790854≈25.5厘米;
f1:f2:f3=(1/λ1):(1/λ2):(1/λ5)=154:120:115;
一、无电离层组合模式/Iono-free/IF:
不同频点电离层延迟关系: L1和L2频点
I2=(f1^2/f2^2)*I1;
I2=(λ2^2/(λ1^2)*I1;
以GPS L1和L2频点为例,介绍无电离层组合:
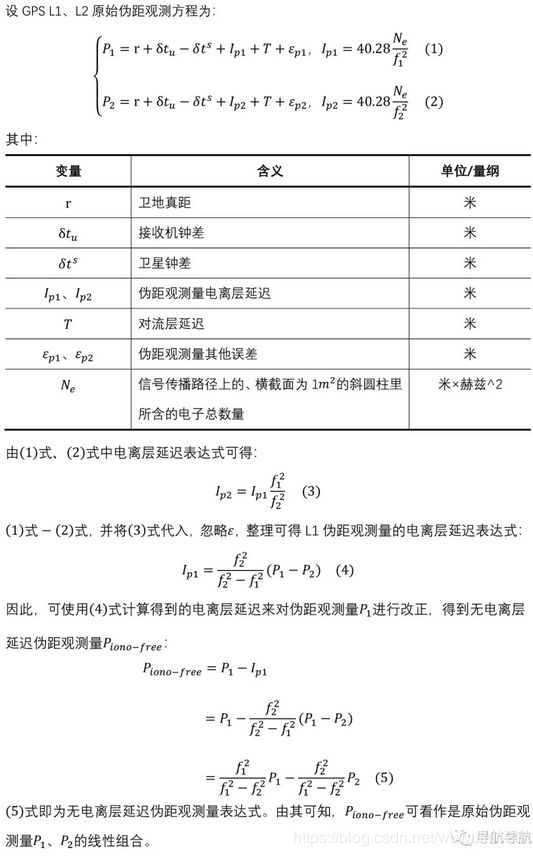
1. IF伪距表达式
推导过程如下:
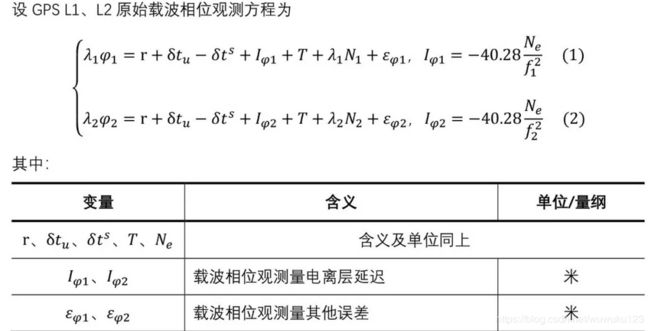
2. IF载波相位表达式:3种
考虑载波相位观测值中,r/卫星-接收机距离为真实距离,既单独将模糊度/N 拿出来构成载波相位观测值;
有两种形式:
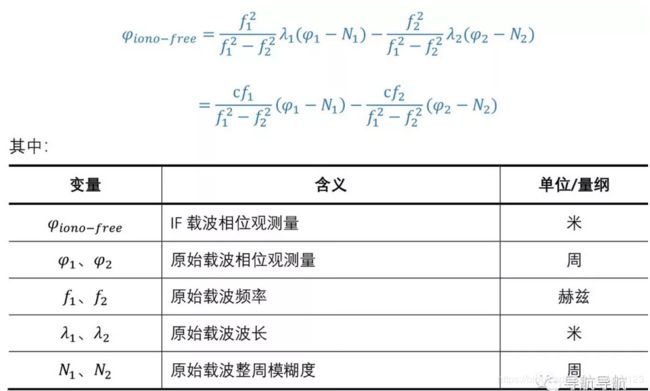
- 形式1:
既无电离层载波为:
- 形式2:
形式1和形式2的区别为:形式1单位为“m”,形式2单位为“Cycle”
推导过程:
- 形式3:
L1、L2载波相位观测值 φ1和φ2,假定是接收机输出的载波值(既模糊度都隐藏在里面),实际数据处理中,拿到的也是这种数据,因此这种形式在实际中用的比较多!
该表达式在各类文献资料中最为常见, 通过对比系数可知, 该式在形式与上文中 IF 载波相位表达式 1 相似, 区别在于, 此处等式右侧的L1、L2载波相位观测量应以米为单位, 若获得的原始载波相位观测量单位为周, 则应将该值乘以各自波长之后再代入, 但这时由于载波相位观测量中的模糊度值并未求出, 因此最终计算得到的 IF 载波相位观测量也受模糊度影响。
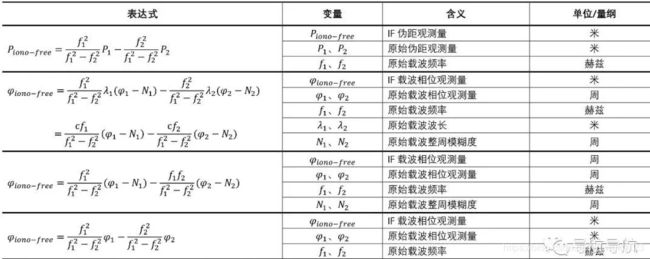
汇总如下:
二、
单频点载波相位测量误差为α;经过双差后,双差测量误差为2α
参考:
《GPS原理与接收机设计》
GPS Iono-free观测量的4种表达式