相对定位中整周模糊度确定方法
一、静态相对定位
1、待定参数法-经典方法
(1)取整法
(2)置信区间法
- XNi为模糊度的实数解
- mXNi=s0(QNiNi)1/2为该参数的中误差
- 置信区间为[XNi- b·mXNi,XNi+ b·mXNi]
- b= xt(f,α/2),根据自由度(f=n-u)和置信水平(1-α),从t分布的数值表中查取。
- 如: f=2500,1-α=99.9%, b =3.28
- 整数解在置信区间之内。
(3)模糊函数法
2、整数解 流程如下:
(1)求初始解
确定基线向量的实数解和整周未知数的实数解
(2)将整周模糊度固定为整数
(3)求固定解
3、实数解
基线较长,误差相关性减弱,初始解的误差将随之增大,从而使模糊度参数很难固定,整数化的意义不大。
二、快速相对定位
走走停停和快速静态定位法是两种具有代表性的快速定位法。
1、走走停停法(Stop and Go)
(1)已知基线法
将已修复周跳、剔除粗差后的双差载波相位观测值组成法方程式,然后将已知的基线向量代入法方程式并求解模糊度参数,最后再用取整法或置信区间法将求得的实数模糊度固定为整数。
(2)交换天线法
2、快速静态定位法
(1)快速模糊度解算法(FARA)
1992年由Frei和Beutler提出,在将模糊度组合代入法方程进行解算前先进行数理统计检验,把大量不合理的组合先剔除,大幅提高计算速度。
搜索候选模糊度
确定最优整数模糊度组合
对备选模糊度组合进行数理统计检验
确认最优解的三项统计检验:
将搜索出来的最优整数模糊度组合,代回原法方程式平差计算,得出基线向量解和方差阵。
1)基线向量的整数解和初始解的一致性检验。
2)整数解和初始解的单位权中误差的一致性检验。
3)整数解中最小单位权中误差与次最小单位权中误差间的显著性检验。
三、实时相对定位
1、初始化法
运动载体处于静止状态时与地面基准站一起通过“初始化”来确定整周模糊度,然后运动载体开始运动,进行定位。
2、实时解算模糊度的方法
(1)确定搜索区域
- 坐标搜索法
- 模糊度搜索法
(2)可采用的方法
- 模糊度函数法
- 最小二乘模糊度搜索法
- FARA法
- 快速模糊度搜索滤波法
- LAMBDA法
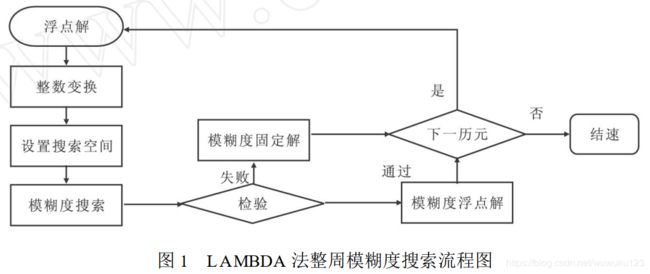
重点介绍LAMBDA方法:
1993年由Teunissen提出,主要思路:
1、为降低模糊度参数之间的相关性而进行的多维整数变换;
2、在转换空间内进行模糊度搜索,再将结果转换回模糊度空间去,求得整数解。
该算法理论严密,搜索速度快、效果好,被广泛采用。
模糊度搜索域分类:
1、观测值域的搜索
2、坐标域的搜索
3、模糊度估值域的搜索
- 模糊度最小二乘搜索法 LSAST-Least Squares Ambiguity Search Technique
- 模糊度快速算法 FARA-Fast Ambiguity Resolution Approach
- 模糊度快速滤波法 FASF-Fast Ambiguity Search Filter
- 模糊度协方差优化分解算法 (优化Cholesky)
- 模糊度最小二乘去相关平差法 LAMBDA
1、整周模糊度求解步骤:
(1)标准最小二乘平差/Kalman 求基线和整周模糊度浮点解;
(2)整数最小二乘估计求整周模糊度固定解;
- 整数去相关变换;
- 整周模糊度搜索———采用的是序贯条件平差的方法。它是目标函数的矩阵分解;
- Ratio检验;
- 整数逆变换求原始模糊度的整数解;
(3)基线固定解
参考:
1、《GPS原理及其应用》
2、《GPS整周模糊度解算的LAMBDA法及程序实现》