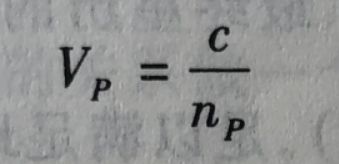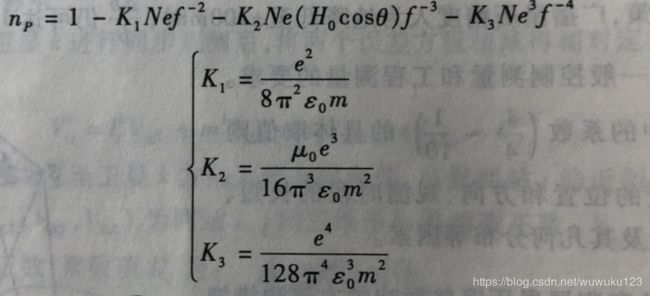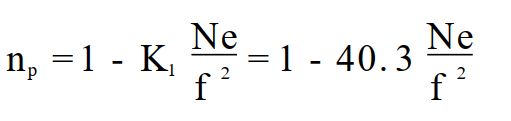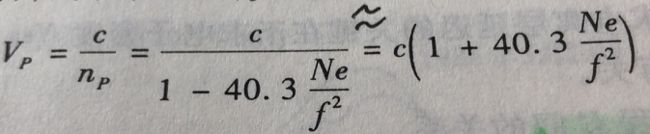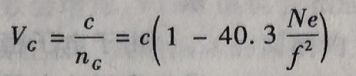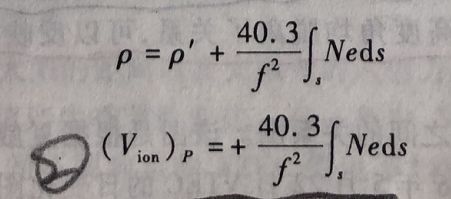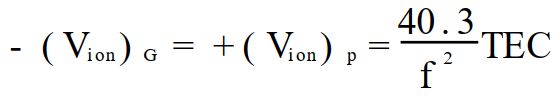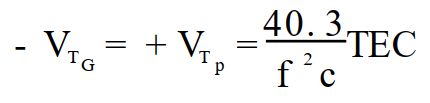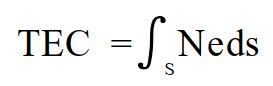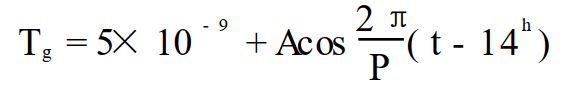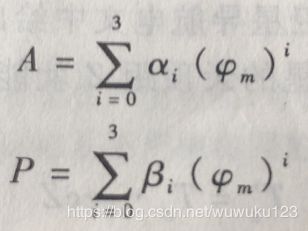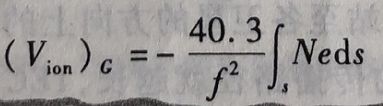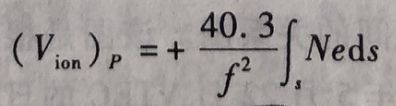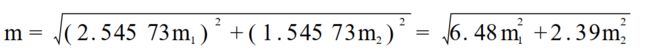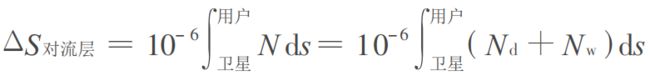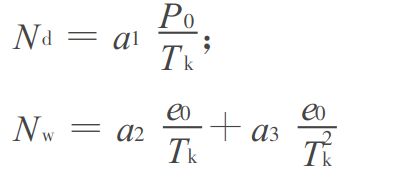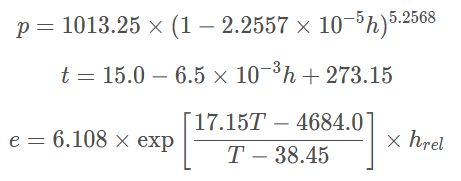卫星导航定位误差之电离层、对流层

一、电离层

       电离层是高度在60~1000KM的大气层，由于太阳紫外线、γ射线等光线的照射导致中性分子被电离，产生正负离子，形成了电离层区域。导致电磁波信号的传播速度发生变化，即产生电离层延迟。

       电磁波在电离层中传播的相速度(单一频率的电磁波的相位的传播速度)Vp与电离层中的相折射率np之间有下列关系:

式中,c为真空中的光速。而相折射率np可表示为: 

Ne:电子密度,即单位体积中所含的电子数,常用电子数/m3或电子数/cm3来表示;
m:电子的质量,m=9.1096×10-31kg;
e:电子所带的电荷值,e=1.6022×10-19c;
ε0:真空中的介电系数,ε0=8.8542×10-12F/m;
H0:地磁场的磁场强度;
μ0:真空中的磁导率;
θ:地磁场的方向与电磁波信号传播方向间的夹角;
f:电磁波信号的频率

忽略上式中的最后两项，简化公式如下：

对GPS卫星信号而言,上式中第二项(f-2项)的值一般为10-6～10-7。故有（约等于下式）:

 

1、延迟计算公式

载波相位在电离层传播速度为相速度，即Vp

伪距在电离层传播速度为群速度，即Vg；

由于存在电离层延迟，从卫星到接收机的几何距离P为：

载波：

伪距：

既：电离层距离延迟改正Vion与总电子含量TEC间有下列关系;(TEC在下面介绍)

电离层延迟，单位：距离：

电离层延迟，单位：时间：

 

2、电子密度Ne与总电子含量TEC

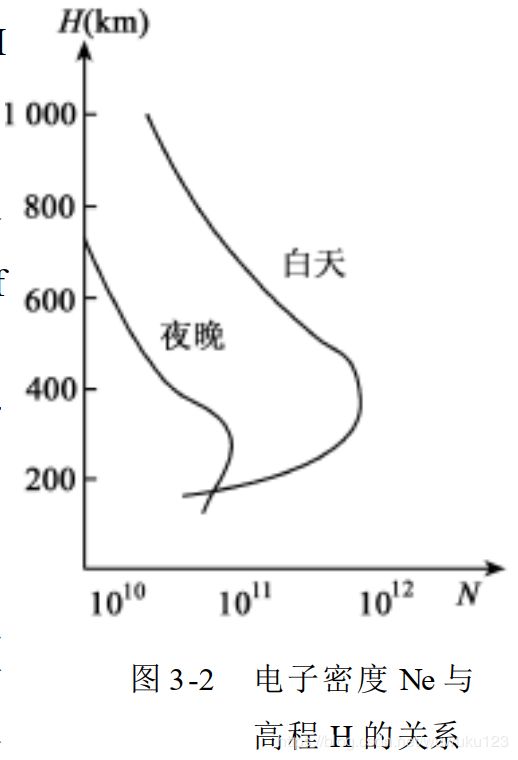
电子密度Ne(单位体积中所含的电子数)与高程、时间的关系；

其中：总电子含量TEC与NE的关系如下：

      总电子含量TEC即为沿卫星信号传播路径s对电子密度Ne进行积分所获得的结果，也即底面积为一个单位面积沿信号传播路径贯穿整个电离层的一个柱体中所含的电子数，通常以电子数/m2或电子数/cm2为单位。此外，我们以10^16个电子/m^2作为TEC的单位，并将它称为1TECU。

       对同一电离层而言,从某一测站至各卫星的方向上的TEC值是不相同的。卫星的高度角h越小。卫星信号在电离层中的传播路径就越长，TEC的值就越大。在该站所有的TEC值中有一个最小值，即天顶方向(h=90°)的总电子含VTEC(VerticalTotalElectronContent)。VTEC与高程和卫星高度角均脱离了关系，可以反映测站上空电离层的总体特征,所以被广泛应用。

3、电离层模型和经验改正公式

此处重点介绍卫星广播星历中使用的Klobuchar/克罗布歇模型

1、计算公式  单位：时间/s

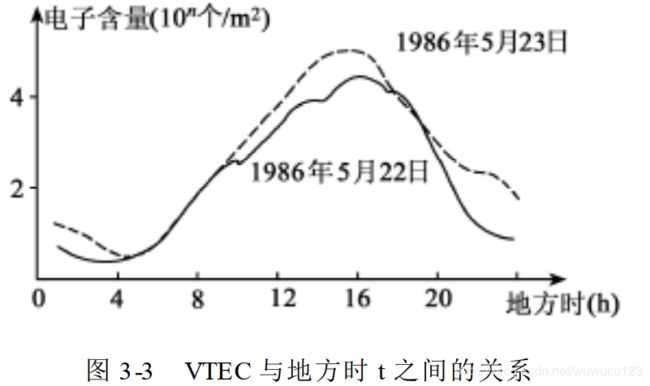
       这是一个被单频GPS用户所广为采用的电离层延迟改正模型。该模型将晚间的电离层时延视为常数,取值为5ns,把白天的时延看成是余弦函数中正的部分。于是天顶方向调制在L1载波(f=1575.42MHz)上的测距码的电离层时延Tg可表示为:

振幅A和周期P分别为：

2、计算方法：

       此模型在计算电离层延迟时，将整个电离层压缩为一个单层，整个电离层中的自由电子都集中在该单层上，称为中心电离层。中心电离层离地面的高度通常取359km。

首先明确的是：Klobuchar模型计算的是天顶星下点这条“线段”的延迟，最后求出后，还需要利用倾斜因子/天顶角正割进行转换。

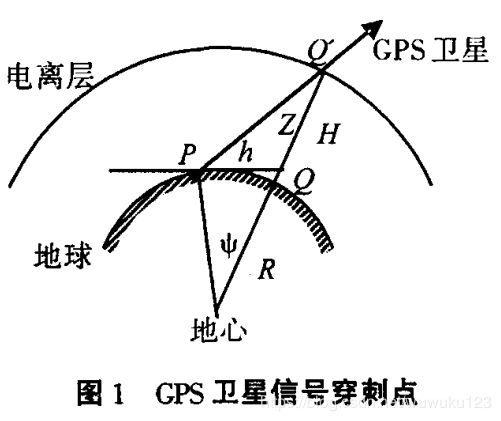
       如图1所示Klobuchar模型采用了单层电离层模型，即把电离层的所有自由电子看作位于高度H(350一400km)厚度忽略的单层球壳上．把GPS卫星和用户P的连线与电离层的交点称作信号穿刺点Q‘，其星下点为Q；P与Q点的地心角用 φ 表示，GPS卫星对于用户P点的地平高度角为h；广播星历中发播的天顶电离层改正的参数的 α 和 β 值，是对于星下点Q的天顶而言的（既QQ'方向）。

• 计算用户P与穿刺点Q‘的地心角φ；
• 计算穿刺点的星下点Q的地理/地心经纬度φQ，λQ；
• 将星下点Q的地理纬度换算为地磁纬度；
• 换算穿刺点的星下点Q处的地方时tQ；
• 计算单频信号的电离层天顶延迟T‘；
• 利用倾斜因子计算信号实际路径的电离层延迟 单位：时间/s

4、双频改正模型

由一下两式可知，伪距和载波电离层延迟（单位：米），卫星信号所受到的电离层延迟是与信号频率f的平方成反比的

双频伪距无电离层表达式：

噪声为：

设测码伪距观测值ρ′1和ρ′2的测量噪声分别为m1和m2,则经双频电离层改正后的距离ρ的噪声将扩大为:

如果，m1=m2；则m=3*m1;即噪声扩大三倍。

GNSS中多频观测值的组合形式

对于载波相位的双频无电离层模型，参考上述链接；

同时，由于双频无电离层延迟组合观测值，整周模糊度非整数，所以通过构建方程，进行变换，得到以L1载波整周模糊度和宽巷模糊度组合形式。

5、顾及信号在卫星内的时延差后的电离层延迟改正公式

也就是Tgd项，关于详细的描述详见《GPS测量与数据处理》第二版，P61；

6、利用GNSS双频观测资料建立VTEC模型

       利用双频观测值不但可确定不同频率的观测值所受到的电离层延迟进而消除其影响,而且可测定穿刺点(卫星信号传播路径与中心电离层的交点)上的VTEC值。

几种VTEC模型

1、IGS所提供的VTEC格网图；

2、CODE的球谐函数模型；

7、利用三频观测量进行电离层延迟改正

二、对流层延迟

1、对流层延迟分析      

卫星导航定位中的对流层延迟通常是泛指电磁波信号在通过高度在50km以下的未被电离的中性大气层时所产生的信号延迟。对流层延迟 80%～90% 是由于大气中干燥气体引起的,称为干分量；其余10%～20%是由水蒸气引起的，称为湿分量。

对流层延迟随对流层折射率而变 , 折射率取决于当地的温度、压力和相对湿度。对流层延迟引起的路径长度差用折射率表示为：

上式中的积分是沿信号传播的路径,这里定义N为折射率。Nd、Nw分别定为在标准海平面的干燥分量折射率和潮湿折射率,与大气的压力、温度和湿度有如下近似关系

式中,P0为在标准海平面干燥分量的大气压力(mbar);Tk为在标准海平面的绝对温度,Tk=Tc+273.2(K);e0为在标准海平面的水蒸气分压力(mbar);a1、a2、a3为经验常数,分别是-12.92K/mbar和371.90K2/mbar。

2、对流层延迟修正

目前对对流层延迟有多种数学模型，这些模型一般都包括两步操作：

第一步：对天顶路径的对流层延迟进行估计；

第二部：对不同仰角下的路径延迟乘上一个倾斜因子/F；

典型的对流层延迟修正模型有霍普菲尔德(Hopfield)模型和萨斯塔莫宁(Saastamoinen)模型。
两个模型求出的对流层延迟均为(沿天顶方向电磁波传播路径延迟/sin(E))，即信号传播路径上的对流层延迟。
一般都采用标准气象元素法进行对流层延迟修正；

详情见P112 《GPS测量与数据处理》

此处，以RTKLIB代码为例，采用的是 Saastamoinen模型

标准大气层模型可以表示为：

其中 h 是海拔高度，hrel​ 是相对湿度，p 为大气压力，e 为大气中的水汽压力，T 为大气温度。

一般对流层模型中，将对流层天顶总延迟（ZTD：Zenith Total Delay）分为对流层静力学延迟（ZHD：Zenith Hydrostatic Delay）和对流层湿延迟（ZWD：Zenith Wet Delay）。静力学延迟约占总延迟量的90%，可以通过实测气压和气温来计算，而湿延迟影响因素较多，不太容易估算。
根据 Saastamoinen 模型，对流层延时 Tr​ 可以表示为静力学延迟 Th​ 与 湿延迟 Tw​ 的和：

其中 z=π/2−el 为天顶角，el 为卫星仰角。

下面摘录了 RTKLIB 中用 Saastamoinen 模型计算对流层延时的函数代码，可以跟以上公式进行一一对应。需要注意的是计算时的单位换算，azel[0], azel[1]分别是方位角和仰角，pos[0], pos[1]分别是接收机纬度和经度，它们的单位都是弧度，pos[2]为接收机高度，单位为米。

/* troposphere model -----------------------------------------------------------
* compute tropospheric delay by standard atmosphere and saastamoinen model
* args   : gtime_t time     I   time
*          double *pos      I   receiver position {lat,lon,h} (rad,m)
*          double *azel     I   azimuth/elevation angle {az,el} (rad)
*          double humi      I   relative humidity
* return : tropospheric delay (m)
*-----------------------------------------------------------------------------*/
extern double tropmodel(gtime_t time, const double *pos, const double *azel,
                        double humi)
{
    const double temp0=15.0; /* temparature at sea level */
    double hgt,pres,temp,e,z,trph,trpw;

    if (pos[2]<-100.0||1E4

 

3、高精度GPS测量时所用的对流层延迟改正方法

1、将对流层延迟当作待定参数

指的是测站天顶方向对流层延迟，为待定参数；总共一个参数。

2、采用随机模型

4、投影函数

信号传播路径上的对流层延迟STD与测站天顶方向的对流层延迟ZTD间有下列关系：

STD=m*ZTD;

m称为投影函数，它是卫星高度角E以及其他一些因素的函数。

其中，投影函数大体分为两类：

• 利用以前的观测资料建立起来的经验模型；

代表为：NMF模型、GMF模型；

• 需要实际气象资料的模型；

代表为：VMF1模型；

 

参考：

1、《GPS测量与数据处理》

2、《Klobuchar模型的解读》

3、《GPS定位误差中对流层延迟的分析》

4、电离层、对流层改正模型对基线解算的影响

5、电离层TEC建模的基本理论与方法

6、《GPS定位中4种对流层延迟修正模型适应性分析》