机器学习入门之多项式曲线拟合

多项式曲线拟合

机器学习和人工智能是最近几年特别火的领域，比如微软小冰、微软cortana、苹果siri、谷歌Now和alphaGo都使用了机器学习，使得他们的产品变得更加智能。
当然除了这些科技巨头，其实我们日常中也可能会使用到人工智能的产品，比如最常见的就是app上的个性化推荐，通过多维度分析用户的个性，给用推荐合适的内容，当然我个人是很讨厌推荐的，基本不点开看。下面我将分为两个部分来阐述多项式曲线拟合。

• 什么是多项式曲线拟合
• 如何评估拟合结果

---

1、什么是多项式曲线拟合

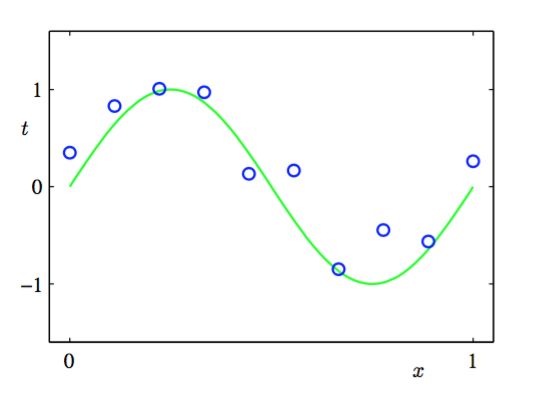
首选我们以一个回归的例子展开阐述，现在假设给定一个训练集。这个训练集由x的N次观测组成,写作 ≡ (x1,…,xN)T,伴随这 对应的t的观测值,记作 ≡ (t1, …, tN )T，图1展示了由N = 10个数据点组成的图像。图1.2中 的输入数据集合 通过选择xn(n = 1, … , N)的值来生成。这些xn均匀分布在区间[0, 1],目标数 据集 的获得方式是:首先计算函数sin(2πx)的对应的值,然后给每个点增加一个小的符合高斯分布的随机噪声。

现在我们输入一个新值x来预测相应的t值。首选我们需要通过训练得出的多项式为y(x,w)，y(x,w)是一个多项式：

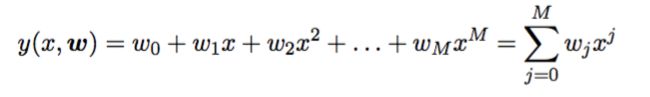
y(x,w)是曲线多项式，它是一个逼近我们真实曲线的多项式。

2、如何评估拟合结果

在上式y(x,w)中M是多项式的阶数(order),xj表示x的j次幂。多项式系数w0,…,wM整体记作向量w。 注意,虽然多项式函数y(x, w)是x的一个非线性函数,它是系数w的一个线性函数。通过最小化误差函数 (error function)来衡量了对于任意给定的w值,函数y(x, w)与训练集数据的差别。如图所示：

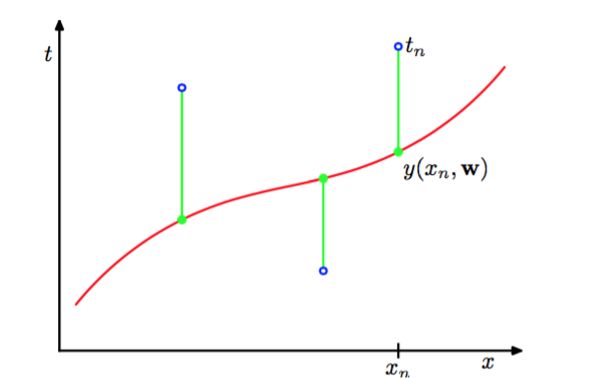
那么我可以知道误差函数为：

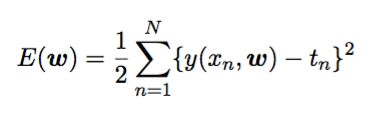
其中1/2是为了方便计算引入的。
我们可以通过选择使得E(w)尽量小的w来解决曲线拟合问题。由于误差函数是系数w的二次函数,因此它关于系数的导数是w的线性函数,所以误差函数的最小值有一个唯一解,记 作w∗,可以用解析的方式求出。最终的多项式函数由函数y(x, w∗)给出。

从图中我们可以看出M=0和M=1拟合效果很差，我们称之为欠拟合，M=3拟合看起来和真实 的曲线差不多，但是当M=9的时候，拟合曲线激烈震荡，我们称之为过拟合。如此看来，曲线拟合的泛化性和M的取值有直接的关系，而M得值我们称之为模型特征个数，比如说房子的价格和房子面积有关系，和房子方向（南北向）有关系，那么面积是房子价格数学模型中的一个特征，房子方向也是一个特征。
为了定量考察泛化性和M之间的关系，我们额外考虑一个测试集，这个测试集由100个数据 点组成,这100个数据点的生成方式与训练集的生成方式完全相同，但是在目标值中包含的随机 噪声的值不同。对于每个不同的M值，我用用根均方(RMS)来表示测试误差：

其中，除以N让我们能够以相同的基础对比不同大小的数据集,平方根确保了E_RMS与目标 变量t使用相同的规模和单位进行度量。下图展示了不同M值和E_RMS的关系：

从中我们可以看到，M=3-8测试误差和训练误差都比较低。能够取得较好的效果。
对已一个给定的模型复杂度,当数据集的规模增加时,过拟合问题变得不那么严重。另一种表 述方式是,数据集规模越大,我们能够用来拟合数据的模型就越复杂(即越灵活)。一个粗略的启发是,数据点的数量不应该小于模型的可调节参数的数量的若干倍(比如5或10)。下图是使用M = 9的多项式对M = 15个数据点(左图)和N = 100个数据点(右图)通过最小化平方和 误差函数的方法得到的解。我们看到增大数据集的规模会减小过拟合问题。

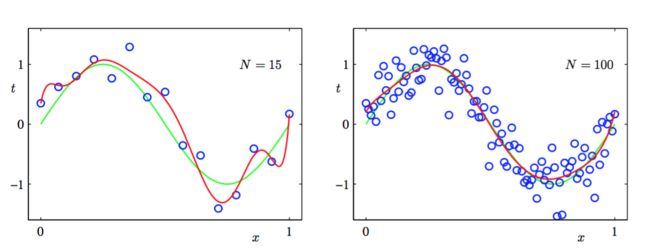
因此，我们了解到增加数据可以减小过拟合问题。但是我们又引来新的问题，那就是不得不根据可得到的训练集的规模限制参数的数量。也可以说是根据待解决的问题的复杂性来选择模型的复杂性。我们可能期望建立相对复杂和灵活的模型，所以我们经常用来控制过拟合现象的一种技术是正则化(regularization)。这种技术涉及到给误差函数增加一个惩罚项,使得系数不会达到很大的值。这种惩罚项最简单的形式采用所有系数的平方和的形式。

其中∥w∥^2 ≡ wT w = w0^2 + w1^2 + … + wM^2 ,系数λ控制了正则化项相对于平方和误差项的重要性，被称之为正则化系数。通过引入正则化项可以减少过拟合的问题。下图是正则化系数对过拟合影响图：

使用正则化的误差函数，用M = 9的多项式拟合图中的数据集。其中正则化参数λ选择 了两个值,分别对应于ln λ = −18和ln λ = 0。因此引入正则化项也可以减少过拟合问题。

总结

在多项式虚线拟合过程中，我们遇到了两个问题，一个是欠拟合，一个是过拟合，对于欠拟合我们只需要增加参数（或者说特征）是拟合更加好，对于过拟合，我们提到了两种方式来解决，一个是增加数据，通过增加数据的方式增加引入更多的特征从而减少过拟合，另一种是增加正则化项。