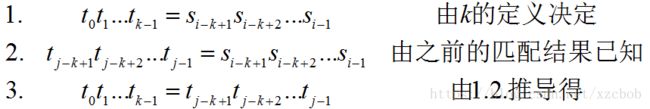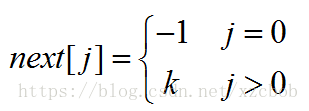简谈 KMP 算法的思路(附 C++ 代码)
KMP算法是由DEKnuth,JHMorris和VRPratt同时发现的,因此人们将这种算法命名为克努特 - 莫里斯 - 普拉特操作(简称KMP算法)。
为了后面叙述方便,在此先说明几个文章中提到的相关概念和约定:
- 字符串模式匹配:寻找某个字符串(子串)在另一个字符串(主串)中第一次出现的位置。
- 模式串:即子串
- 串中的字符从0开始编号
穷举法
在叙述KMP算法之前,我们先来了解一下字符串模式匹配的最容易想到的方法,即穷举法。
穷举法的思路就是,逐个比较两个字符串的相应位置当匹配失败时则从头重新开始,具体过程大致如下:
如主串:ababcabcacbab子串:abcac
从0号字符开始第一次匹配:
ababcabcacbab
a
第二次匹配:
ababcabcacbab
ab
第三次匹配:
ab a bcabcacbab
ab c
观察到两个字符不相等,所以从主串的1号字符开始匹配:
a b abcabcacbab
a
观察到两个字符不相等,所以从主串的2号字符开始匹配:
ababcabcacbab
a
接下来进行多次匹配之后:
ababca b cacbab
abca c
观察到两个字符不相等,于是又要从主串的3号字符开始匹配......
由此我们可以大致观察到,传统暴力穷举解法当匹配失败时都要从头重新开始,我们设想一种最坏的情况,即每次都匹配到模式串的最后一个字符才发现不同。我们假设主串的长度为m,子串的长度为n,所以传统穷举解法的时间复杂度为O(m * n)
附C ++代码如下:
#include
#include
using namespace std;
int strindex(string s,string t)
{
//函数功能:在主串s中找到子串t首次出现的位置
//若找到则返回位置下标(下标从0开始),若未找到则返回-1
int i,j;
for(i=0;i=t.length())
return i;
}
return -1;
}
int main()
{
string s;//主串
string t;//子串
cin>>s;
cin>>t;
//s='ababcabcacbab'
//t='abcac'
cout< KMP算法
在介绍KMP算法之前,我们先观察一下上面的匹配过程,重点观察每次匹配失败倒回的情况。
第一次匹配失败:
ab a bcabcacbab
ab c
由于字符ab之前已经匹配过了,于是我们思考是否可以跳过某些比较过程,直接将子串右移过来而不倒回主串的位置,如下:
ababca b cacbab
abca c
按照这种思路,我们可以不对主串字符的定位进行回移,从而得到一种时间复杂度为O(M + N)的方法。
接下来我们就要思考这样几个问题:
- 按照这种做法,是不是每次匹配失败之后都直接将子串的开头拉到主串的相应位置直接进行匹配就可以了呢?
- 如果不是,应该将子串拉到什么位置比较合适呢?
首先解答第一个问题:
还是上述的字符串,我们来看这次的匹配:
ababca b cacbab
abca c
匹配失败了,倘若直接将子串的开头拉到主串的相应位置,我们就应该这样匹配:
ababca b cacbab
a bcac
然后接着匹配下去,我们可以得出子串在主串中没有出现过,然而这个结论显然是错误的。
接着解答第二个问题:
假设匹配过程中,主串的第我个字符与字串中的第j个字符不一样,并且我们接下来要将子串的第k个字符重新与主串的第i个字符进行比较(相当于先把子串的开头拉到主串的下面,再左移k位),我们可以得到k应该满足以下几个条件(t为子串,s为主串):
公式看起来比较繁琐,简单来说就是模式串开头的k个字符要和j前面(左边)的k个字符完全一样。而且我们得到了k只与子串自身有关,与主串无关由此。我们可以求出字串中每个字符对应的k值,并称为next数组。
以上即为KMP算法的思路,由于众人的习惯和风格不同,对于next数组的求解有不同的理解和具体实现,下面仅提供一种处理方法。
以字符串:abaabcac为例,
next = -10011201
以左数第一个c为例:
ab a ab c ac
开头两个字符和c前面的两个字符相同,所以对应的next值为2,其他字符也可以用同样的方法验证。
那么为什么该方法中next[0] == - 1呢?
我们以主串:abbbcabcacbab子串:abaabcac 为例(只是说明为什么next[0]要等于-1,所以最后求出结果是否包含子串也没有什么影响啦(* ^▽^ *))
我们来看匹配过程:
abaa c abcacbab
abaa b
因为b所对应的next值为1
所以将子串拉到c下面之后再左移一位进行匹配得:
abaa c abcacbab
a b
因为b对应的next值为0
所以将子串拉到c下面进行匹配得:
abaa c abcacbab
a
在这里如果不对模式串的第一个字符a的next值进行特殊标记的话,程序在运行的时候会进入死循环,所以需要让next[0] = - 1,从而可以继续向后匹配。
附C ++代码如下:
#include
#include
using namespace std;
int kmp(string s,string t)
{
//函数功能:同上
int i=0,j=-1;
int slen=s.length(),tlen=t.length();
int next[tlen];
//首先求出模式串t的next数组
next[0]=-1;
while(i>s;
cin>>t;
//s='ababcabcacbab'
//t='abcac'
cout< 以上就是文章的全部内容,希望可以帮到大家,文章内容如有不足或者错误,恳请大家批评指正。
PS:最近发现正文里的不少英文单词都乱码了,如果大家遇到问题的话可以评论下,多谢了