python绘制基本初等函数图像
之前用python绘制了笛卡尔直角坐标系，绘制了指数函数，绘制了对数函数，有了这三个基础工作的积累，本期，将研究如何利用python把六类基本初等函数一劳永逸的绘制出来。
基本初等函数概念
简单的说基本初等函数是不能再由其他更简单结构的函数通过加减乘除四则运算来结合而成的函数。在数学里，基本初等函数包括幂函数、指数函数、对数函数、三角函数、反三角函数、常数函数一共6类。基本初等函数均是连续函数，这使得其图形看起来是连贯的，前面已经介绍过指数函数和对数函数，现在把六类函数的形状和定义域和值域整理。
常数函数
一般的，形如
的函数称为常数函数，其中c为任意实数，故常数函数的定义域和值域均为全体实数R。
幂函数
一般地，形如
的函数称为幂函数，幂函数的定义域和值域均为全体实数R。
指数函数
一般地，形如
的函数称为幂函数，其中a>0, a≠1，指数函数的定义域为全体实数R，值域为（0，+∞）。
对数函数
一般地，形式
的函数称为对数函数，其中a>0, a≠1，指数函数的定义域为（0，+∞），值域为全体实数R。
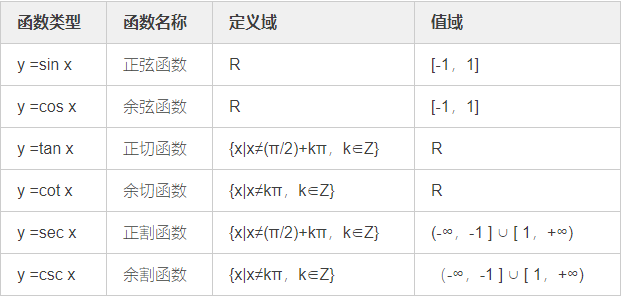
三角函数
常见的三角函数有
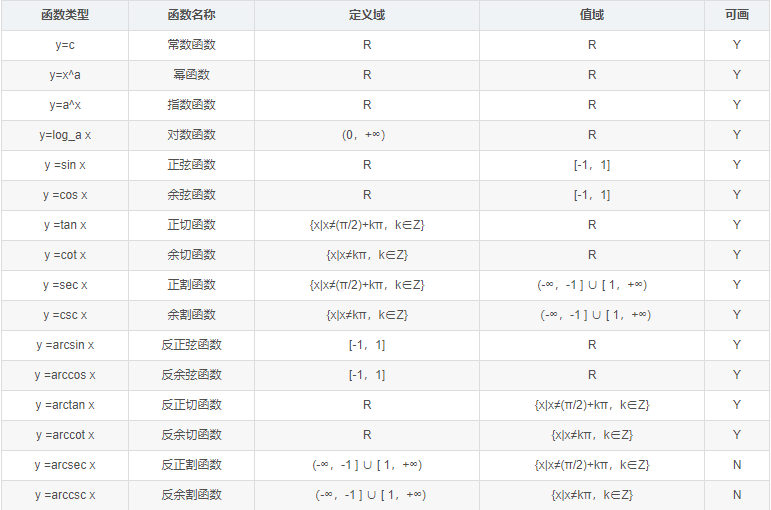
反三角函数
常见的反三角函数主要有以下 6 个
完整代码
知道不同函数的定义非常关键，因为这直接决定了我们画图时候的横坐标可取值范围，先把所有典型函数列出来
我们需要实现的功能是，我们输入一个函数表达式，程序给我们返回该表达式的图像，完整代码如下
# -*- coding: utf-8 -*-
"""
Created on Sun Feb 16 16:10:09 2020
project name:draw_func_figure
@author: 帅帅de三叔
"""
import math #导入绘图模块
import numpy as np #导入数值计算模块
import matplotlib.pyplot as plt #导入绘图模块
plt.rcParams['font.sans-serif']=['SimHei'] #绘图中文
plt.rcParams['axes.unicode_minus']=False #绘图负号
import mpl_toolkits.axisartist as axisartist #导入坐标轴加工模块
def elementary_func_draw(X, expr): #定义绘制函数图形的函数,其中x是自变量，y为因变量
#X=np.linspace(-10, 10, 100) #自变量
Y=list(map(lambda x:eval(expr), X))
fig=plt.figure(figsize=(4, 4)) #新建画布
ax=axisartist.Subplot(fig, 111) #使用axisartist.Subplot方法创建一个绘图区对象ax
fig.add_axes(ax) #将绘图区对象添加到画布中
ax.plot(X, Y, label=expr) #绘制函数图形
ax.axis[:].set_visible(False) #隐藏原来的实线矩形
ax.axis["x"]=ax.new_floating_axis(0, 0, axis_direction="bottom") #添加x轴
ax.axis["y"]=ax.new_floating_axis(1, 0, axis_direction="bottom") #添加y轴
ax.axis["x"].set_axisline_style("->", size=1.0) #给x坐标轴加箭头
ax.axis["y"].set_axisline_style("->", size=1.0) #给y坐标轴加箭头
plt.xlim(-max(X), max(X)) #设置横坐标范围
plt.ylim(-max(Y), max(Y)) #设置纵坐标范围
ax.text(-1.0, max(Y), 'y', fontsize=12) #标注y轴
ax.annotate(s='x', xy=(max(X), 0), xycoords='data', xytext=(+0, +5), textcoords='offset points', fontsize=12) #标注x轴
plt.legend()
plt.show()
plt.savefig("func_figure.png")
if __name__=="__main__":
expr=input("请输入函数表达式：")
if "log" in expr: #画对数函数
X=np.linspace(0.001, 10, 100)
elif "asin" in expr: #画反正弦函数
X=np.linspace(-1, 1, 100)
elif "acos" in expr: #画反余弦函数
X=np.linspace(-1, 1, 100)
else:
X=np.linspace(-10, 10, 100)
elementary_func_draw(X, expr)
接下来就是见证奇迹的时候
当我输入
2
便会画出如下图
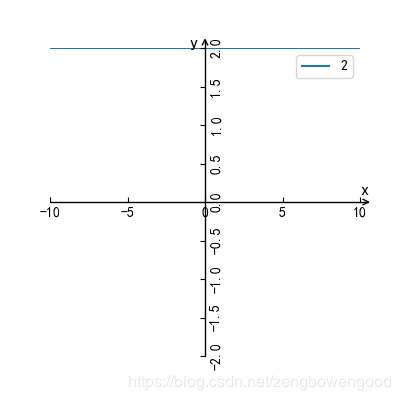图 1 y=2
当我输入
x**2
便会画出如下图
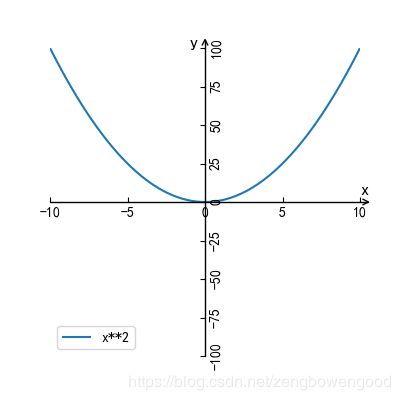图 2 y=x^2
当我输入
2**x
便会画出如下图
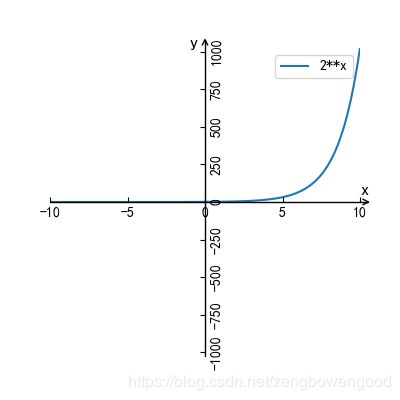图 3 y=2^x
当我输入
math.log(x, 2)
便会画出如下图
图 4 y=log_2 x
当我输入
math.log10(x)
便会画出如下图
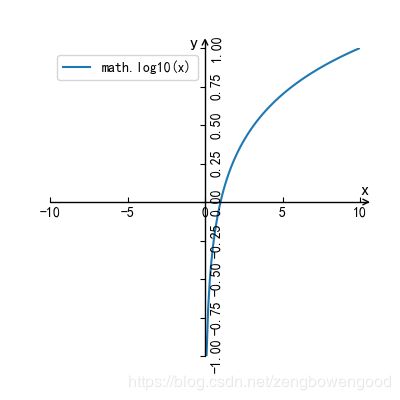图 5 y=log_10 x
当我输入
math.log(x)
便会画出如下图
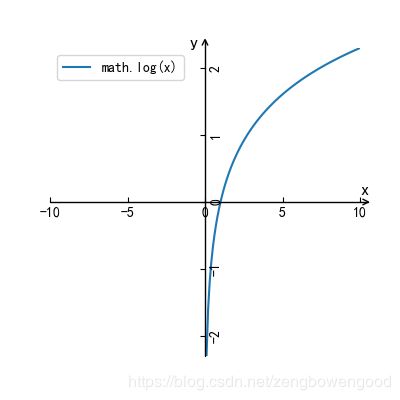图 6 y=ln(x)
当我输入
math.sin(x)
便会画出如下图
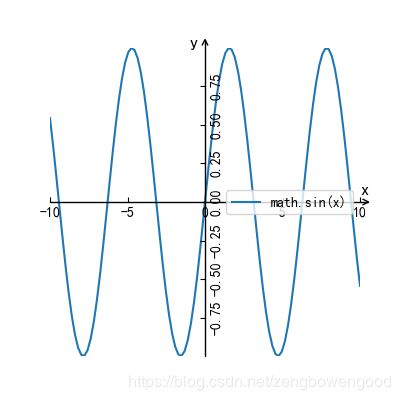图 7 y=sin(x)
当我输入
math.cos(x)
便会画出如下图
图 8 y=cos(x)
当我输入
math.tan(x)
便会画出如下图
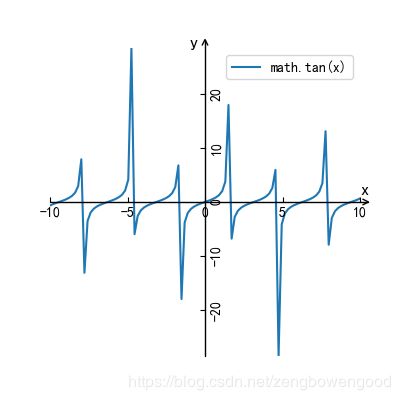图 9 y=tan(x)
当我输入
1/math.tan(x)
便会画出如下图
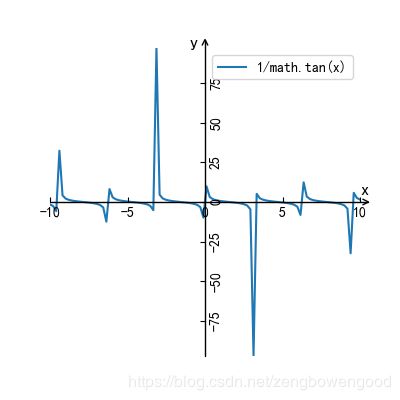图 10 y=cot(x)
当我输入
1/math.cos(x)
便会画出如下图
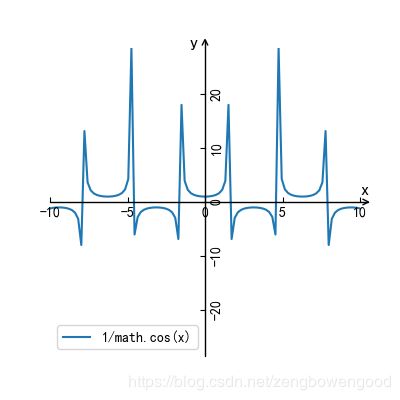图 11 y=sec(x)
当我输入
1/math.sin(x)
便会画出如下图
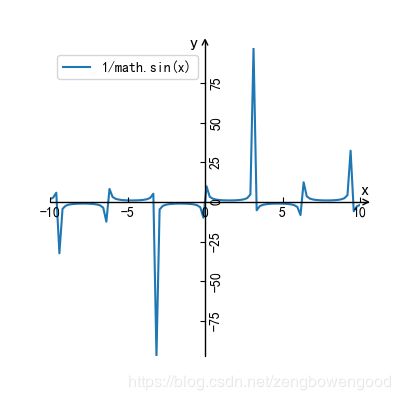图 12 y=csc(x)
当我输入
math.asin(x)
便会画出如下图
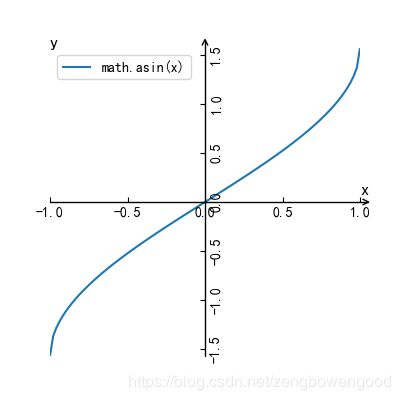图 13 y=arcsin(x)
当我输入
math.acos(x)
便会画出如下图
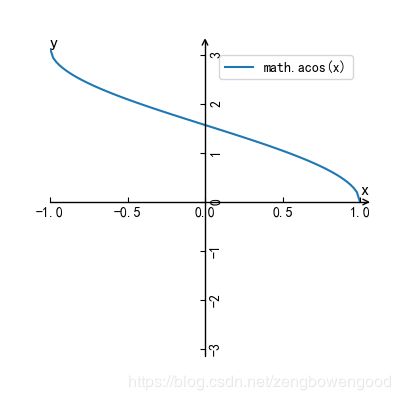图 14 y=arccos(x)
当我输入
math.atan(x)
便会画出如下图
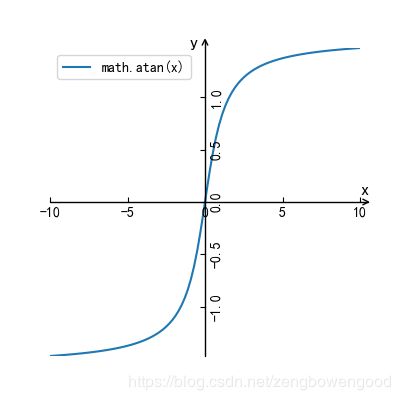图 15 y=arctan(x)
当我输入
math.pi/2-math.atan(x)
便会画出如下图
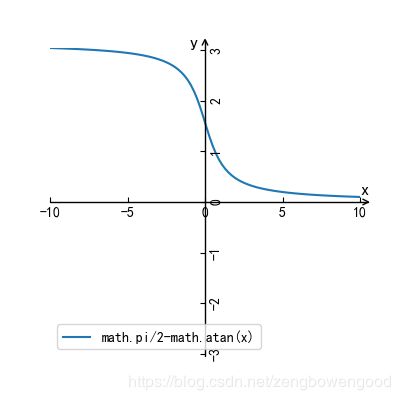图 16 y=arccot(x)
当我输入
arcsec(x)
糟糕，不出图，囧！
当我输入
arccsc(x)
糟糕，不出图，二囧！
这两个函数还有待后面解决，或许通过三角函数关系式，或者重单独重新定义这两个函数，如果你有什么好办法，欢迎留言。
代码解释
这里重点解释一下在给两个坐标轴打标签时候的处理方法
ax.text(-1.0, max(Y), 'y', fontsize=12) #标注y轴
ax.annotate(s='x', xy=(max(X), 0), xycoords='data', xytext=(+0, +5), textcoords='offset points', fontsize=12) #标注x轴
在对y轴标注的时候，位置的横向，我们选定了一个定值 -1.0 ，纵向选择Y的最大值，因为横向是定下来的，从-10到10，故只需要在Y轴稍微偏左一点即可，而纵向是随着横向变化而变化的，最大莫过于max(Y)，故取其最大值。
在对x轴标注的时候，我们不在用到text()函数，改用annotate()函数，因为这个函数更为灵活
其中
s='x' 表示要标注的内容；
xy=(max(X), 0)是为标注设置一个参照点（max(X), 0），即横坐标的最右端；
xycoords='data' 表示参照点的单位是一个值的形式；
xytext=(+0, +5)表示标注文本的偏移量，是相对于参照点的偏移量；
textcoords=‘offset points’表示注释文本的坐标系属性，表示以点为单位，也可以是pixels，表示以像素为单位，还可以是xycoords的属性值
因为选定了横坐标最右端为参照点，再加上偏移量，任你y轴怎么变化，这个标注会老老实实呆在那个离（max(X), 0）不远处。
如果你还有不懂的地方欢迎来“三行科创”微信公众号留言，同时交流群免费向大家开放，入群讲缘分。
参考文献
1，百度百科：基本初等函数
2，百度百科：反余切函数
3，math模块
- - -The end- - -
你可能喜欢
指数函数
笛卡尔第十三封情书
python绘制指数函数
python绘制笛卡尔直角坐标系
国家中小学网络云平台数学电子教材
三行科创微信公众号欢迎投稿，提供线索
稿件聚焦数学、逻辑，数学工程，数学文化等领域
一经采用，我们将奉上酬劳
投稿邮箱：[email protected]
商务合作：17521754388
加入交流群，添加微信：melite01(备注 交流群)
