计算机图像学学习记录(二) —— 中点画线算法
中点画线算法
为了方便阅读算法代码的人,现在这贴上算法核心代码:
算法过程:
注意:本过程只针对,斜率绝对值小于1的情况。
void DDADrawLine::MPDrawLine(int x0, int y0, int x1, int y1)
{
int a, b, dt1, dt2, d, x, y;
a = y0 - y1;
b = x1 - x0;
d = a + a + b; //为了避免小数,这里取2倍 不写成2*a + b的原因是防止乘法
dt1 = a + b + a + b;
dt2 = a + a;
x = x1;
y = y1;
// 绘制起点
// glColor3f(1.0f, 0.0f, 0.0f);
glBegin(GL_POINTS);
glVertex2i(x, y);
// glEnd();
// 绘制整条线
while (x < x1)
{
if (d < 0)
{
x++;
y++;
d += dt1;
}
else
{
x++;
d += dt2;
}
glBegin(GL_POINTS);
glVertex2i(x, y);
glEnd();
}
}
如果针对全部斜率的情况,该算法改进结果如下:
void DDADrawLine::MPLineDraw(int x0, int y0, int x1, int y1)
{
int x = x0, y = y0;
int a = y0 - y1;
int b = x1 - x0;
int cx = (b >= 0 ? 1 : (b = -b, -1));
int cy = (a <= 0 ? 1 : (a = -a, -1));
// glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0f, 0.0f, 0.0f);
glBegin(GL_POINTS);
glVertex2i(x, y);
glEnd();
int d, d1, d2;
if (-a <= b) // 斜率绝对值 <= 1
{
d = a + a + b;
d1 = a + a;
d2 = a + a + b + b;
while (x != x1)
{
if (d < 0)
{
y += cy;
d += d2;
}
else
{
d += d1;
}
x += cx;
glBegin(GL_POINTS);
glVertex2i(x, y);
glEnd();
}
}
else // 斜率绝对值 > 1
{
d = a + b + b;
d1 = b + b;
d2 = a + a + b + b;
if (d < 0)
{
d += d1;
}
else
{
x += cx;
d += d2;
}
y += cy;
glBegin(GL_POINTS);
glVertex2i(x, y);
glEnd();
}
}
原理
中点画线算法采用直线的一般式方程:
F ( x , y ) = 0 A x + B y + C = 0 A = − ( Δ y ) ; B = ( Δ x ) ; C = − B ( Δ x ) \begin {aligned} F(x, y) = 0 \\Ax + By + C = 0 \\A = -(\Delta y); B = (\Delta x); C = -B(\Delta x) \end {aligned} F(x,y)=0Ax+By+C=0A=−(Δy);B=(Δx);C=−B(Δx)
对于不同的点,我们可以利用其值和0进行比较来筛选。
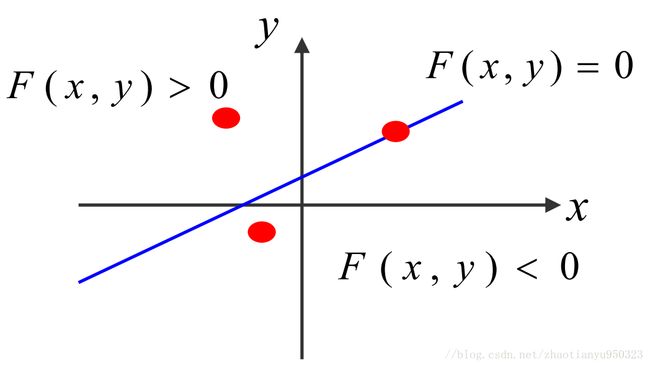
- 对于直线上的点 F ( x , y ) = 0 F(x, y) = 0 F(x,y)=0
- 对于直线上方的点 F ( x , y ) > 0 F(x, y) > 0 F(x,y)>0
- 对于直线下方的点 F ( x , y ) < 0 F(x, y) < 0 F(x,y)<0
所以,中点画线算法在每次最大位移方向上走一步,而另外一个方向是走步还是不走,需要利用中点误差项来进行判断。
我们假定: 0 ≤ ∣ k ∣ ≤ 1 0\leq|k|\leq1 0≤∣k∣≤1。 因此,每次x方向上加1, y 方向上是否加1取决于函数值与中点方位。

当M在Q的下方,则 P u P_u Pu离直线比较近,应为下一个像素点。
当M在Q的上方,则 P d P_d Pd为下一点。
那么我们如何判断M是在Q的上方还是下方呢?
我们就需要把M代入到理想直线方程中:
F ( x m , y m ) = A x m + B y m + C F(x_m, y_m) = Ax_m + By_m + C F(xm,ym)=Axm+Bym+C
KaTeX parse error: Expected & or \\ or \cr or \end at position 40: … F(x_m, y_m) \\\̲ ̲&=F(x_i + 1, y_…
当 d > 0的时候, M在Q的上方,取 P u P_u Pu
当 d < 0的时候, M在Q的下方,取 P d P_d Pd
当 d = 0的时候, 取 P d P_d Pd取 P u P_u Pu都可以
那么我们可以得到中点画线法的基本原理,公式如下:
y = { y + 1 d < 0 y d ≥ 0 y = \begin {cases} y + 1 & d < 0 \\ y & d\geq0 \end {cases} y={y+1yd<0d≥0
算法改进
我们来分析一下该算法的计算量
y = { y + 1 d < 0 y d ≥ 0 d i = A ( x i + 1 ) + B ( y i + 0.5 ) + C y = \begin {cases} y + 1 & d < 0 \\ y & d\geq0 \end {cases} \\ d_i = A(x_i + 1) + B(y_i + 0.5) + C y={y+1yd<0d≥0di=A(xi+1)+B(yi+0.5)+C
我们发现,为了求出d的值,需要进行两个乘法,四个加法。似乎比DDA算法大了很多的计算量,那么我们该如何改进呢?
我们将利用求d的递推公式,将计算量简化为一个整数加法级别。
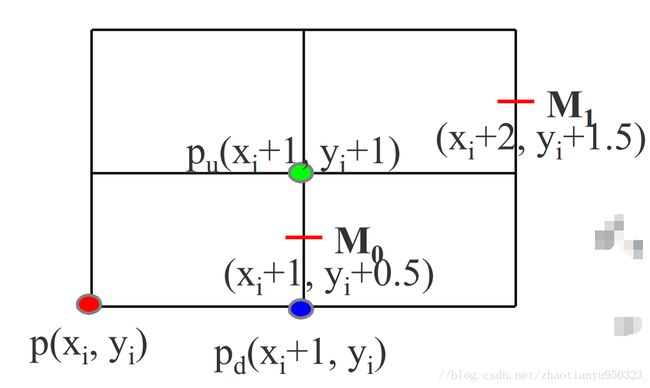
对于上面这种情况:
KaTeX parse error: Expected & or \\ or \cr or \end at position 49: …}, y_{m_0}) \\\̲ ̲&=F(x_i + 1, y_…
KaTeX parse error: Expected & or \\ or \cr or \end at position 49: …}, y_{m_1}) \\\̲ ̲&=F(x_i + 2, y_…
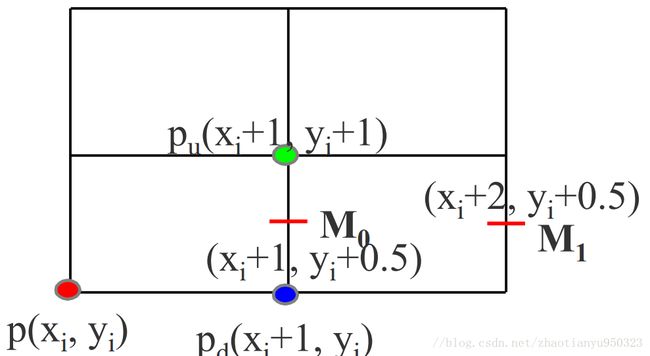
对于上面这种情况:
KaTeX parse error: Expected & or \\ or \cr or \end at position 49: …}, y_{m_1}) \\\̲ ̲&=F(x_i + 2, y_…
接下来我们计算d的初始值:
KaTeX parse error: Expected & or \\ or \cr or \end at position 52: …y——0 + 0.5) \\\̲ ̲&= A(x_0 + 1) +…
那么,可以得到:
d n e w = { d o l d + A + B d < 0 d o l d + A d ≥ 0 d 0 = A + 0.5 B d_{new} = \begin {cases} d_{old} + A + B & d < 0 \\ d_{old} + A & d \geq0 &d_0 = A + 0.5B \end {cases} dnew={dold+A+Bdold+Ad<0d≥0d0=A+0.5B
之后再利用2d代替d来摆脱浮点运算,写出仅仅包含整数的算法,这样中点画线算法就提高到了整数加法,优于DDA算法。
接下来来看中点画线算法的代码实现:
图形初始化过程:
// 实现DDA画线算法测试
// author: 赵天宇
// date : 2018/03/09
void DDADrawLine::MPTest(int argc, char **argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE);
using namespace std;
// cout << "输入线段起始和终点坐标(范围 0 - 500, 0 - 500):";
// cin >> xs >> ys >> xe >> ye;
srand((unsigned)time(NULL));
xs = random(0, 500);
ys = random(0, 500);
xe = random(0, 500);
ye = random(0, 500);
glutInitWindowPosition(50, 100);
glutInitWindowSize(500, 500);
glutCreateWindow("Digital Differential Analyser Line");
glClearColor(1.0, 1.0, 1.0, 1.0);
glMatrixMode(GL_PROJECTION);
gluOrtho2D(0.0, 500, 0.0, 500.0);
glutDisplayFunc(DDADrawLine::display);
DDADrawLine::myInit();
// DDADrawLine::MPDrawLine(xs, ye, xe, ys);
glutMainLoop();
}
显示过程:
void DDADrawLine::display(void)
{
glClear(GL_COLOR_BUFFER_BIT); /*clear the window */
/*----------------------------------------*/
/* viewport stuff */
/*----------------------------------------*/
/* set up a viewport in the screen window */
/* args to glViewport are left, bottom, width, height */
glViewport(0, 0, 500, 500);
/* NB: default viewport has same coords as in myinit, */
/* so this could be omitted: */
// DDADrawLine::DDALine(xs, ys, xe, ye);
DDADrawLine::MPDrawLine(xs, ys, xe, ye);
/* and flush that buffer to the screen */
glFlush();
}
算法过程:
注意:本过程只针对,斜率绝对值小于1的情况。
void DDADrawLine::MPDrawLine(int x0, int y0, int x1, int y1)
{
int a, b, dt1, dt2, d, x, y;
a = y0 - y1;
b = x1 - x0;
d = a + a + b; //为了避免小数,这里取2倍 不写成2*a + b的原因是防止乘法
dt1 = a + b + a + b;
dt2 = a + a;
x = x1;
y = y1;
// 绘制起点
// glColor3f(1.0f, 0.0f, 0.0f);
glBegin(GL_POINTS);
glVertex2i(x, y);
// glEnd();
// 绘制整条线
while (x < x1)
{
if (d < 0)
{
x++;
y++;
d += dt1;
}
else
{
x++;
d += dt2;
}
glBegin(GL_POINTS);
glVertex2i(x, y);
glEnd();
}
}
如果针对全部斜率的情况,该算法改进结果如下:
void DDADrawLine::MPLineDraw(int x0, int y0, int x1, int y1)
{
int x = x0, y = y0;
int a = y0 - y1;
int b = x1 - x0;
int cx = (b >= 0 ? 1 : (b = -b, -1));
int cy = (a <= 0 ? 1 : (a = -a, -1));
// glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0f, 0.0f, 0.0f);
glBegin(GL_POINTS);
glVertex2i(x, y);
glEnd();
int d, d1, d2;
if (-a <= b) // 斜率绝对值 <= 1
{
d = a + a + b;
d1 = a + a;
d2 = a + a + b + b;
while (x != x1)
{
if (d < 0)
{
y += cy;
d += d2;
}
else
{
d += d1;
}
x += cx;
glBegin(GL_POINTS);
glVertex2i(x, y);
glEnd();
}
}
else // 斜率绝对值 > 1
{
d = a + b + b;
d1 = b + b;
d2 = a + a + b + b;
if (d < 0)
{
d += d1;
}
else
{
x += cx;
d += d2;
}
y += cy;
glBegin(GL_POINTS);
glVertex2i(x, y);
glEnd();
}
}
运行结果:

参考文献:
【1】 中国大学MOOC 中国农业大学 计算机图形学课程 计算机图形学
【2】 画线算法博客 - 只缘心高嫌地窄 画线算法
【3】 中点画线法(计算机图形学)- 时光足迹 中点画线法
声明:本文的主要内容来自[1], 如有违权将立即删除。