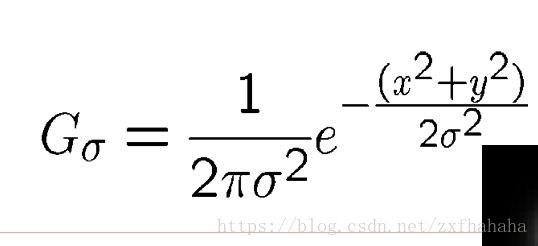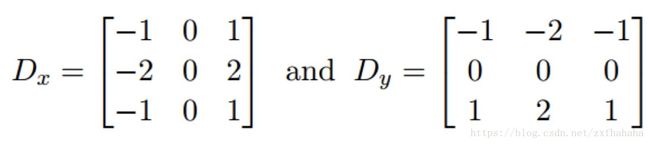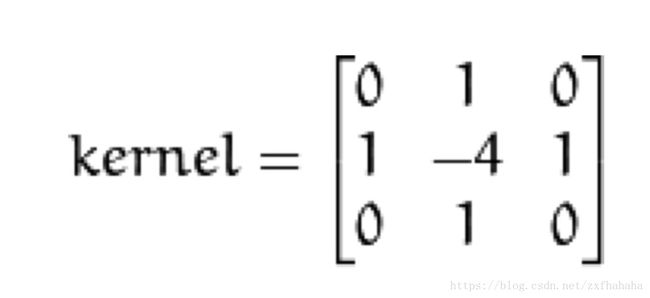【计算机视觉】4.图像滤波和边缘检测
滤波/卷积
滤波/卷积概念
在每个图片位置（x, y）上进行基于邻域的函数计算。
邻域
对x，y进行加减数后的结果，通俗来讲就是某一点周围的几个点
滤波函数
1.这里滤波函数相当于一个遮罩，是实现对邻域进行计算的方法，可以理解为通过滤波函数对图片某一位置邻域进行权重相加。
2.滤波函数又叫做卷积核、卷积模板；滤波器、滤波模板；扫描窗。其中卷积核是最常用的说法。
3.不同功能需要定义不同的函数
- 图像增强
①平滑/去燥
②梯度/锐化 - 信息提取、检测
①边缘、显著点、纹理
②模式
滤波计算公式
滤波结果为滤波函数和像素邻域值乘积和
参数解释：
•x, y是像素在图片中的位置/坐标
•k, l是卷积核中的位置/坐标，其中心点的坐标是（0,0）
•f[k, l]是卷积核中在（k, l）上的权重参数
•I[x+k, y+l]是与f[k, l]相对应的图片像素值
•h[x, y]是图片中(x, y)像素的滤波/卷积结果
如下图，当x，y=0时，也就是中心位置是(0,0)。此位置的邻域就是加减k和l，
当k，l=1时（0，0）的邻域就是下面的9个位置。
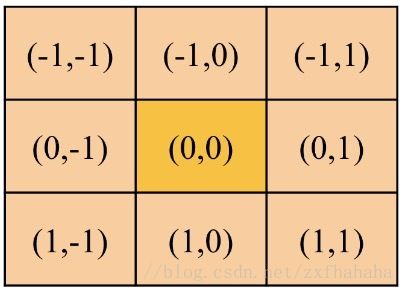
卷积的操作如下图所示，图片上圈的红框就是卷积核要操作的邻域。例子中卷积核每个位置上的值都为1，因此进行卷积就是把图片上的9个值分别乘上对应卷积核上的值1再求和，4*1+1*1+6*1+7*1+2*1+3*1+9*1+5*1+8*1=45。
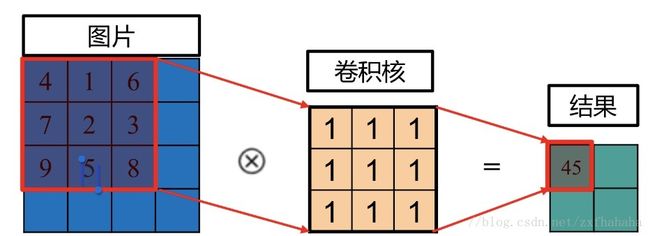
卷积核移动一个步长后继续进行上述的卷积操作，如下图的4步就可以得到一个2*2矩阵，这就是卷积的结果。
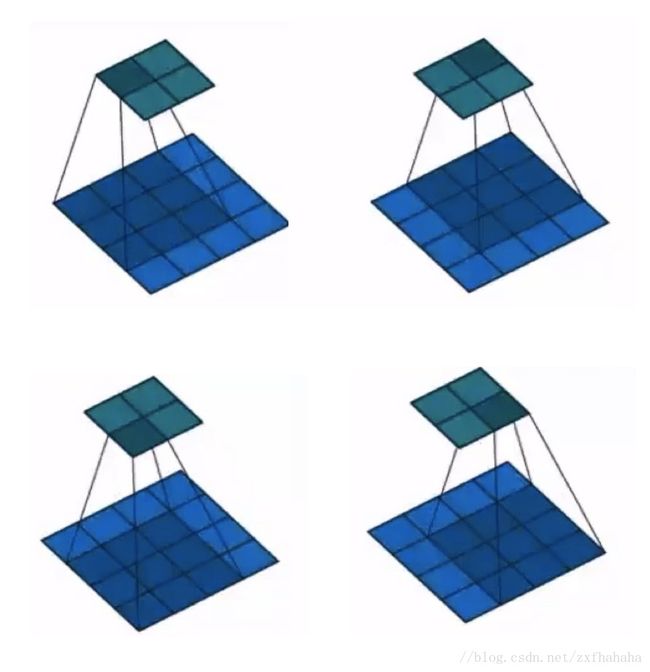
边界补充
由上面介绍的卷积操作可以看出，结果比原来图像小了，那么如果要获得同尺寸输出，则要进行边界补充。 因为卷积核越大，得到的结果就越少，所以要补充的就越多。
那进行补充的值为多少呢，下面将介绍4中补充的类型。
我们以7x7卷积：3x3补充成9x9为例。
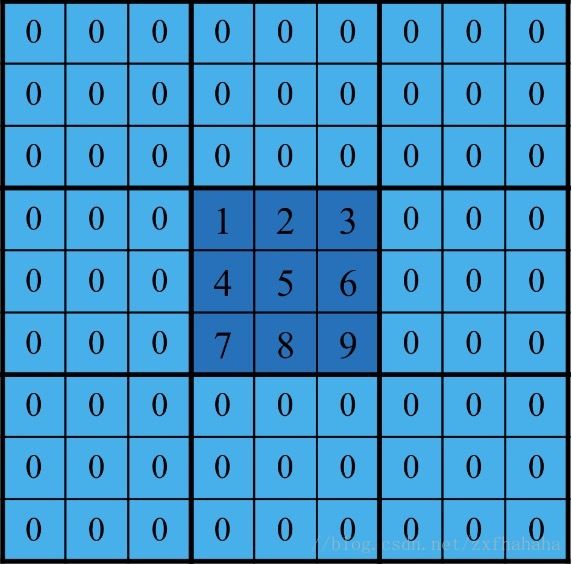
补零（zero-padding）
补零很简单，就是把缺失的地方都补成0
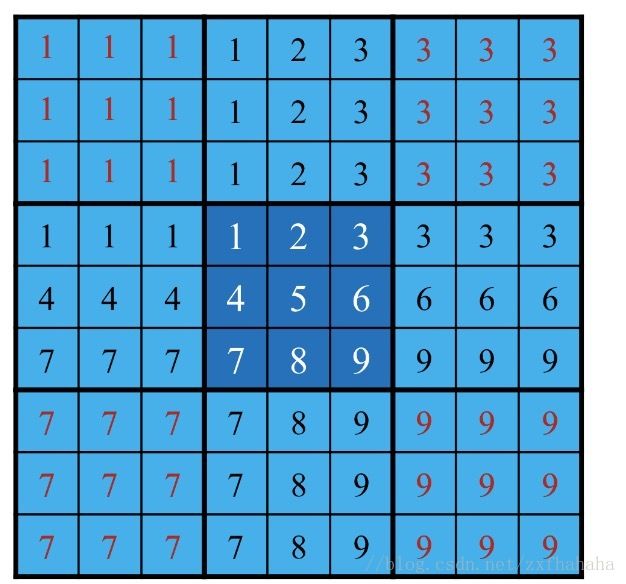
边界复制（replication）
边界复制就是离哪个值近就填充成什么
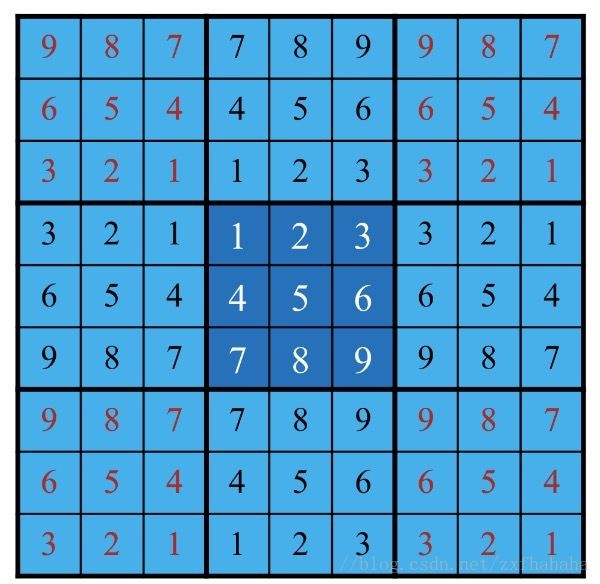
镜像（reflection）
每个区域都进行镜像操作
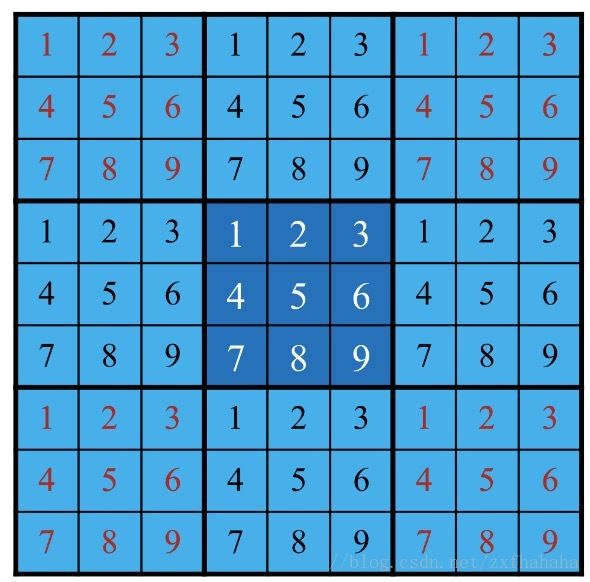
块复制（wraparound）
图像滤波和边缘检测都是通过卷积核来进行操作的，下面来看一下图像滤波和边缘检测具体的卷积核是什么。
图像滤波
图像滤波作用
•滤波是处理图像数据的常用基础操作
•滤波操作可以去除图像中的噪声点，由此增强图像的特征
可以根据卷积核的不同把图像滤波分为好多种。如中值滤波，高斯滤波和均值滤波。
中值滤波
中值滤波就是找到中位数作为卷积结果，因此中值滤波选择奇数尺寸作为卷积核，如3x3，5x5，7x7，2n-1 x 2n-1
操作原理
•卷积域内的像素值从小到大排序
•取中间值作为卷积输出
如下图，把图片中的卷积域内的像素值从小到大排序后，5在中间为中位数，因此结果为5
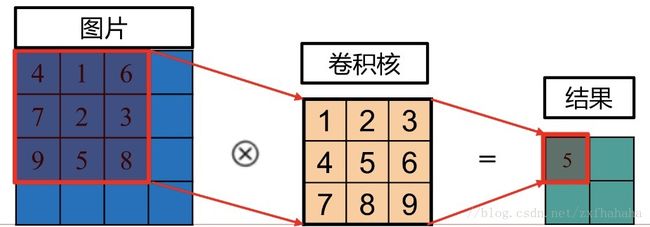
作用
中值滤波能够有效去除椒盐噪声
Python中使用中值滤波 cv2.medianBlur()
cv2.medianBlur(img,卷积核大小)
参数：
img：图片
参数2：滤波尺寸，也就是卷积核大小，为奇数
例子：
img = cv2.imread('./images/nosiy_image.jpg', cv2.IMREAD_GRAYSCALE)
med1 = cv2.medianBlur(img, 3) # 3x3中值滤波
med2 =cv2.medianBlur(img, 5) # 5x5中值滤波
# 图像对比
cv2.imshow('img', img)
cv2.imshow('med1', med1)
cv2.imshow('med2', med2)
cv2.waitKey(0)
cv2.destroyAllWindows()高斯滤波
高斯滤波就是把卷积核中的数换成符合高斯分布的值，即中间数值最大，越往两边数值越小。高斯滤波的卷积核要为奇数尺寸，如3x3，5x5，7x7，2n-1 x 2n-1
操作原理
模拟人眼，关注中心区域。
人眼特性：离关注中心越远，感受精度越模糊
作用
有效去除高斯噪声。
当关心图像整体而不是细节问题时可以用高斯滤波。
高斯函数
高斯滤波的基础就是高斯函数，看下图有几个高斯函数，有两个参数 μ和σ 。期望值μ决定高斯函数的位置，标准差σ 决定高斯函数的胖瘦，σ 越小越瘦，关注的区域越集中
高斯函数的二维公式如下：
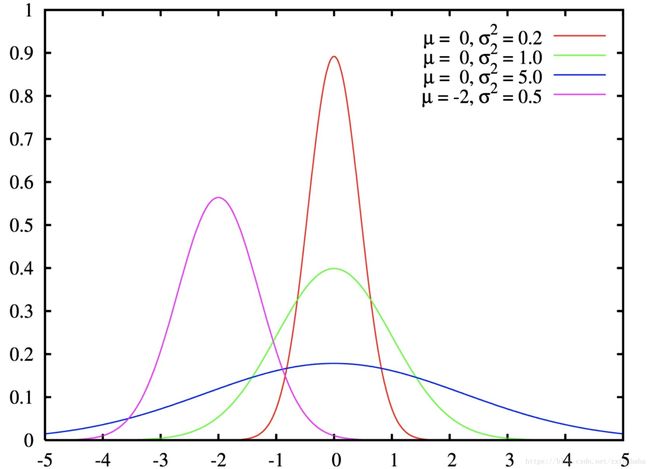
参数：
•x, y是卷积参数坐标
•标准差σ
画出的二维高斯函数如下图所示
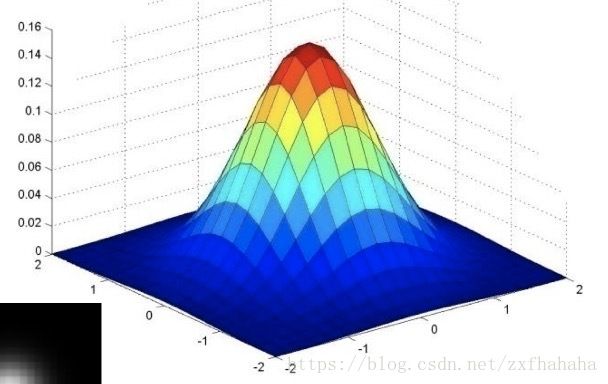
高斯滤波的σ
σ越小，关注区域越集中。在图像中的表现如下图
对一张图片做高斯滤波，σ分别为1和4时结果如下图。可见σ越大关注区域越不集中，看起来就越模糊
Python-opencv中使用高斯滤波
cv2.GaussianBlur(img, (3, 3), 0)
参数1：img 图像
参数2：卷积核的长和宽（奇数）。注意和其他滤波不同
参数3：沿x与y方向的标准差(如果只给x，y=x，如果都给0，那么函数会自己计算)。这个参数也决定了结果的模糊程度。
img = cv2.imread('./images/camera.jpg', cv2.IMREAD_GRAYSCALE)
gas1 = cv2.GaussianBlur(img, (3, 3), 0) # 3x3
gas2 = cv2.GaussianBlur(img, (5, 5), 0) # 5x5
# 图像对比
cv2.imshow('img', img)
cv2.imshow('gas1', gas1)
cv2.imshow('gas2', gas2)
cv2.waitKey(0)
cv2.destroyAllWindows()均值滤波
均值滤波方法是，对待处理的当前像素，用卷积核的均值来替代原像素的值的方法。卷积核为奇数尺寸，如3x3，5x5，7x7，2n-1 x 2n-1。卷积核的参数和为1.
操作原理
对于3 *3卷积核来说，就是对待处理的当前像素乘上对应的权系数矩阵模板。
g = (f(x-1,y-1) + f(x,y-1)+ f(x+1,y-1) + f(x-1,y) + f(x,y) + f(x+1,y) + f(x-1,y+1) + f(x,y+1) + f(x+1,y+1))/9
Python-opencv中使用均值滤波cv2.blur()
cv2.blur(img, (3, 3), 0)
举个例子
img = cv2.imread('./images/camera.jpg', cv2.IMREAD_GRAYSCALE)
mean1 = cv2.blur(img, (3, 3), 0) # 3x3
mean2 = cv2.blur(img, (5, 5), 0) # 5x5
# 图像对比
cv2.imshow('img', img)
cv2.imshow('mean1', mean1)
cv2.imshow('mean2', mean2)
cv2.waitKey(0)
cv2.destroyAllWindows()边缘检测
图像梯度
1.图像梯度是由图像导数表示的，灰度图像I中亮度值的变化可以描述为x方向、y方向上的导数Ix, Iy。
2.图像梯度为向量:
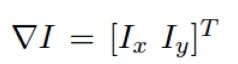
3.图像梯度包含两个重要的属性：
①大小： 用来描述亮度值变化的强度
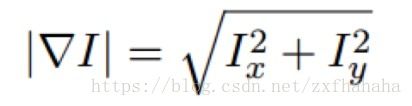
②梯度角（gradient angle）
描述每个像素点最大亮度变化的方向，可通过numpy.arctan2()计算。
图像导数的计算是通过离散估计得出的，即在x方向，y方向上进行以下的卷积操作：
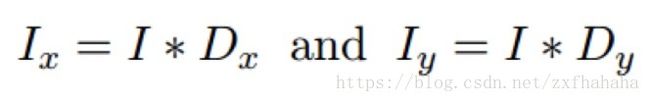
我们可以根据卷积核Dx, Dy的不同，有以下常用的边缘检测方法
Sobel算子
卷积核：
X方向上的边缘检测：
sobelx = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=5)
Y方向上的边缘检测：
sobely = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=5)
Laplacian 算子
laplacian = cv2.Laplacian(img, cv2.CV_64F)
举例：
img = cv2.imread('./images/messi.jpg', cv2.IMREAD_GRAYSCALE)
laplacian = cv2.Laplacian(img, cv2.CV_64F)
sobelx = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=5)
sobely = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=5)
# 图像对比
plt.figure(figsize=(10, 8))
plt.subplot(2,2,1),plt.imshow(img,cmap = 'gray')
plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(2,2,2),plt.imshow(laplacian,cmap = 'gray')
plt.title('Laplacian'), plt.xticks([]), plt.yticks([])
plt.subplot(2,2,3),plt.imshow(sobelx,cmap = 'gray')
plt.title('Sobel X'), plt.xticks([]), plt.yticks([])
plt.subplot(2,2,4),plt.imshow(sobely,cmap = 'gray')
plt.title('Sobel Y'), plt.xticks([]), plt.yticks([])
plt.show()结果：
