表达式计算器（逆波兰法）栈操作（C语言实现）

---

可能很多的同学在学数据结构的时候。说到栈，都会有一道很经典的题目，那就是用栈来实现计算器。我们都知道普通的计算写起来是很简单的，但是如果涉及到左右括号以及加减乘除组成的运算式的时候则写起程序时便不那么容易了。
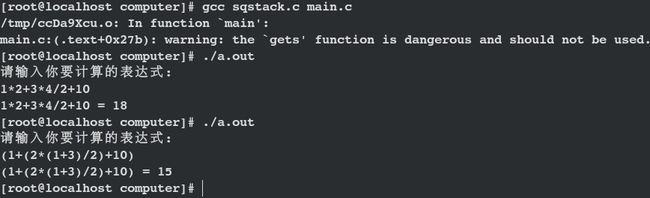
比如：（1+（2*（1+3）/2）+10)
面对上面这个表达式，要想写出这样一个计算器的程序就显得比较困难，有一种先进后出的数据结构———栈就可以很好的解决这个问题。

那么是不是我们有了栈之后就好解决了呢？实际上不是
我们还需要借助一种叫做逆波兰表达式（后缀表达式的思想）

知识补充：逆波兰表达式又叫做后缀表达式。在通常的表达式中，二元运算符总是置于与之相关的两个运算对象之间，这种表示法也称为中缀表示。波兰逻辑学家J.Lukasiewicz于1929年提出了另一种表示表达式的方法，按此方法，每一运算符都置于其运算对象之后，故又称为后缀表示

哈哈，让我们来看几个例子，大家一看就懂了
正常的表达式 逆波兰表达式

a+b ---------> a,b,+

a+(b-c) -----> a,b,c,-,+

a+(b-c)*d ---> a,b,c,-,d,*,+

a+d*(b-c)---->a,d,b,c,-,*,+

a=1+3 -------> a=1,3 +
最后看一下我们的终极例子
（1+（2*（1+3）/2）+10)（中綴表达式）
 1213+*/+10+(逆波兰表达式)

可能会有看不懂的人，我来讲解一下
首先中缀表达式我们是先将1+3然后*2然后再/2,然后+1然后+10
逆波兰呢也是这样的，只是它表达的方式不一样。从左往右开始，遇到符号则把符号前面的两个数字与符号运算，然后再将数字放回。（哈哈，栈的感觉出来了没有），所以也是先将1+3然后*2然后再/2,然后+1然后+10

下面我们来看程序。代码有详细的注释，应该可以满足初学者的需求

---

/* sqstack.h*/
#ifndef SQSTACK_H_
#define SQSTACK_H_

#define MAXSIZE 32
//栈结构体
typedef struct
{
    int data[MAXSIZE];

    int top;
}sqstack;

sqstack *sqstack_create();  //创建栈
int sqstack_push(sqstack *, int ); //入栈
int sqstack_pop(sqstack *, int *); //出栈
int sqstack_top(sqstack *, int *); //查看栈顶值
int sqstack_is_empty(sqstack *); //判断栈是否为控
void sqstack_display(sqstack *); //显示栈内容，调试用的

#endif

/* sqstack.c */
#include 
#include 

#include "sqstack.h"

/* 创建栈 */
sqstack *sqstack_create()
{
    sqstack *L;

    L = (sqstack *)malloc(sizeof(*L));

    L->top = -1;

    return L;
}

/* 入栈 */
int sqstack_push(sqstack *L,int x)
{
    //如果入栈超出栈空间
    if (L->top == MAXSIZE - 1)
    {
    return -1;
    }
    //压栈
    L->data[++L->top] = x;
    return 0;
}

/* 出栈 */
int sqstack_pop(sqstack *L,int *x)
{
    //如果出栈超出栈空间
    if (L->top == -1)
    {
    return -1;
    }
    //利用传出参数传出栈顶元素
    *x = L->data[L->top--];
    return 0;
}

/* 获得栈顶值 */
int sqstack_top(sqstack *L,int *x)
{
    if (L->top == -1)
    {
    return -1;
    }

    *x = L->data[L->top];
    return 0;
}
/* 判断栈是否为空 */
int sqstack_is_empty(sqstack *L)
{
    return (L->top == -1);
}

/* 打印输出栈中元素 */
void sqstack_display(sqstack *L)
{
    int i;
    if (L->top == -1)
    {
    return ;
    }

    for (i = 0 ; i <= L->top; i++)
    {
    printf("%d ",L->data[i]);
    }
    printf("\n");
}

/******************************************************
  日     期: 2015.4.7
  功     能: 计算器的实现:实现加、减、乘、除和左右括号
  作     者: siriuszxn(赵溪楠)
*******************************************************/

#include 
#include "sqstack.h"
#define  MAX 255

//优先级判断函数
int get_pri(int ope)
{
    switch(ope)
    {
    case '(':   return 0;
    case '+':
    case '-':   return 1;
    case '*':
    case '/':   return 2;
    default :   return -1;
    }
}

/* 将两个数出栈、根据ope符号计算，然后再次入栈 */
void compute(sqstack *snum,int ope)
{
    int n,n1,n2;
    //依次获得数值栈的栈顶两个数
    sqstack_pop(snum,&n1);
    sqstack_pop(snum,&n2);
    //计算
    switch(ope)
    {
        case '+':   n = n1 + n2; break;
        case '-':   n = n2 - n1; break;
        case '*':   n = n1 * n2; break;
        case '/':   n = n2 / n1; break;
    }
    //计算完成再次入栈
    sqstack_push(snum,n);
}
/* 只有符号才会进入该函数 */
void deal_ope(sqstack *snum,sqstack *sope,int ope)
{
    int old_ope;
    //如果sope符号栈是空栈或者符号为‘(’
    if (sqstack_is_empty(sope) || ope == '(')
    {
        //将括号(入栈
        sqstack_push(sope,ope);
        return ;
    }
    //获得当前的符号栈的栈顶
    sqstack_top(sope,&old_ope);

    //将当前的符号栈的栈顶符号与传入的符号进行优先级比较
    if (get_pri(ope) > get_pri(old_ope))
    {   
        //传入符号大于当前栈顶，则将传入符号入栈
        sqstack_push(sope,ope);
        return ;    
    }
    //如果传入的符号优先级小于当前栈顶符号
    while (get_pri(ope) <= get_pri(old_ope))
    {
        //将当前栈顶的符号取出与数字栈中顶端的两个数字进行计算
        sqstack_pop(sope,&old_ope);
        compute(snum,old_ope);
        //如果计算完毕之后符号栈为空则break;
        if (sqstack_is_empty(sope))
        {
            break;
        }
        //再次取出一个当前栈符号与传入符号比较
        sqstack_top(sope,&old_ope);
    }
    //进行完毕优先级计算之后，再将新传入的符号入栈
    sqstack_push(sope,ope);
}
/*如果检测到符号时')',则执行该函数，参数为数字栈和符号栈*/
void deal_bracket(sqstack *snum,sqstack *sope)
{
    int old_ope;
    //获得当前的符号栈的栈顶符号
    sqstack_top(sope,&old_ope);
    //直到找到预期配对的左括号。因为正确的算式中左右括号一定是配对的
    while (old_ope != '(')
    {
        //当前符号出栈然后将数字出栈两个进行计算,在括号内优先级最高，
        sqstack_pop(sope,&old_ope);
        compute(snum,old_ope);
        //然后再次取出当前符号栈栈顶符号，至到出现‘(’
        sqstack_top(sope,&old_ope);
    }
    //最后将出现的左扩号出栈丢弃
    sqstack_pop(sope,&old_ope);
}


int main()
{
    /*str为表达式数组*/
    char str[MAX];
    printf("请输入你要计算的表达式:\n");
    gets(str);

    int i = 0;
    int value = 0;   //数字的值
    int flag = 0;    
    int old_ope;

    sqstack *snum,*sope;      // 定义两个指向栈结构体的指针

    snum = sqstack_create();  // 创建存放数字的栈

    sope = sqstack_create();  // 创建存放运算符号的栈

    /* 表达式字符串解析函数,然后将高优先级的符号/(*)进行计算重新入栈
       退出while大家的优先级都一样+-*/
    while (str[i] != '\0')
    {
        //获取输入的数字
        if (str[i] >= '0' && str[i] <= '9')//num
        {
            value = value * 10 + str[i] - '0';
            flag = 1;
        }
        else//ope
        {
            if (flag)
            {
                //flag = 1说明value里面存储了数字，将其入栈
                sqstack_push (snum, value);
                //num标志清零，value存放数字的变量清零
                flag = 0;
                value = 0;
            }
            if(str[i] == ')')
            {
                //如果是右括号，则
                deal_bracket(snum,sope);
            }
            else//+-*/(等情况 
            {
                deal_ope(snum,sope,str[i]);
            }   
        }   
        i++;
    }
    //如果flag = 1.说明value里面还有数值,将其入栈 
    if (flag)
    {
        sqstack_push(snum,value);
    }
    //然后将符号与数字依次出栈计算。数字出栈计算完成之后回再次在compute中入栈
    while (!sqstack_is_empty(sope))
    {
        sqstack_pop(sope,&old_ope);
        compute(snum,old_ope);
    }
    //取出数字栈最后剩下的数字，就是最后的答案
    sqstack_pop(snum,&value);
    //打印结果
    printf("%s = %d\n",str,value);

    return 0;
}

演示结果！！！！！！