Java小程序之哈夫曼树与文件压缩和解压缩(一)哈夫曼树构造篇
Java小程序之哈夫曼树与文件压缩和解压缩(一)哈夫曼树构造篇
前言:在了解哈夫曼树之前,我们还是先看下树的相关知识吧!
一、数据结构中树的相关知识
数据结构是 计算机
存储、组织 数据
的方式。数据结构是指相互之间存在一种或多种特定关系的 数据元素
的集
合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储 效率
。数据结构往往同高效的检索 算法
和 索引
技术有关。数据结构主要包含集合、线性结构、树行结构和图行结构;
这次主要看下树形结构:
1、树的定义:树:是由n(n>=1)个有限节点组成一个具有层次关系的集合
2、树的相关术语
节点度:一个节点含有子树的个数称为该节点的度
树的度:一棵树中,最大的节点的度为树的度
叶子节点:度为零的节点
父亲节点:若一个节点含有子节点,则当前节点为改子节点的父亲节点
子节点:一个节点含有子树,则子树的根节点为改节点的子节点
兄弟节点:具有相同父亲节点的子节点互为兄弟节点
节点层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推
树的深度(高度):树中节点最大的层次
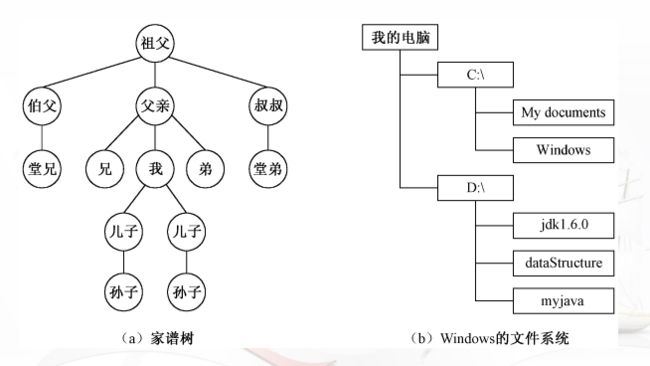
其他:堂兄弟节点、子孙、森林:
节点度:一个节点含有子树的个数称为该节点的度
树的度:一棵树中,最大的节点的度为树的度
叶子节点:度为零的节点
父亲节点:若一个节点含有子节点,则当前节点为改子节点的父亲节点
子节点:一个节点含有子树,则子树的根节点为改节点的子节点
兄弟节点:具有相同父亲节点的子节点互为兄弟节点
节点层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推
树的深度(高度):树中节点最大的层次
其他:堂兄弟节点、子孙、森林:
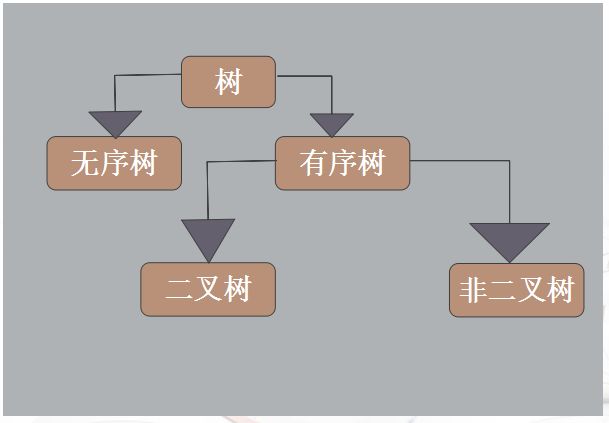
3、树的分类
无序树:树中的节点次序是没有规律的
有序树:指树中同层结点从左到右有次序排列,这样的树称为有序树。
1)二叉树:每个节点最多含有两个子树的树称为二叉树
2)非二叉树:所有不是二叉树的树都属于非二叉树
无序树:树中的节点次序是没有规律的
有序树:指树中同层结点从左到右有次序排列,这样的树称为有序树。
1)二叉树:每个节点最多含有两个子树的树称为二叉树
2)非二叉树:所有不是二叉树的树都属于非二叉树
4、二叉树
定义:二叉树是一种特殊的树形结构,每个节点至多只有两颗子树,并且子树有左右之分,其次序不能随意颠倒,是有序树的一种。
注意:二叉树是由一个根结点、两棵互不相交的左子树和右子树组成。
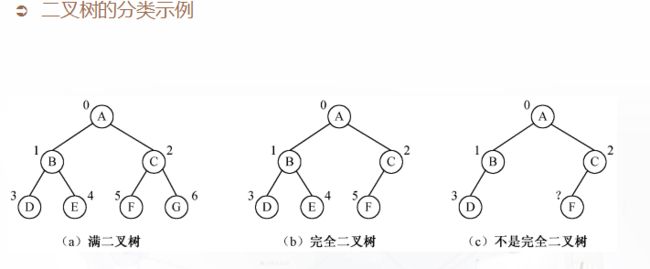
二叉树分类
满二叉树:对于上述的完全二叉树,如果去掉其第d层的所有节点,那么剩下的部分就构成一个满二叉树
完全二叉树:对于一颗二叉树,假设其深度为d(d>1)。除了第d层外,其它各层的节点数目均已达最大值,且第d层所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树;
注意:二叉树是由一个根结点、两棵互不相交的左子树和右子树组成。
二叉树分类
满二叉树:对于上述的完全二叉树,如果去掉其第d层的所有节点,那么剩下的部分就构成一个满二叉树
完全二叉树:对于一颗二叉树,假设其深度为d(d>1)。除了第d层外,其它各层的节点数目均已达最大值,且第d层所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树;
5、完全二叉树性质
若根结点的层次为1,则二叉树第i层最多有2的(i-1)次方个结点。
在高度为k的二叉树中,则最多有2k-1个结点(k≥0)
设一棵二叉树节点个数为n,则父节点个数为n/2。
一棵具有n个结点的完全二叉树,对序号为i(0≤i若i=0,则i为根结点,无父母结点;若i >0,则i的左右子结点序号为:
若2i+1若2i+2
若根结点的层次为1,则二叉树第i层最多有2的(i-1)次方个结点。
在高度为k的二叉树中,则最多有2k-1个结点(k≥0)
设一棵二叉树节点个数为n,则父节点个数为n/2。
一棵具有n个结点的完全二叉树,对序号为i(0≤i
若2i+1
6、哈夫曼树
给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
有关哈夫曼树的术语
路径长度:
节点路径长度:从一个节点(根节点)到另外一个节点所经过的路径的分支数目
树的路径长度:指树种所有节点的路径长度之和
权值:
指的是所有叶子节点的
date
域,存放一个数值,用来表示当前叶子节点的数据,那这个值就是权值
带权路径长度:
所有叶子节点的带权路径长度之和
最优二叉树(哈弗曼树):
1
、通过所有权值节点,形成一个二叉树,最终这个二叉树的带权路径最小,则此二叉树是哈夫曼树(最优二叉树)
2
、树的结构不止一个,同一层的节点,可以左右替换
构造哈夫曼树的思路:
1、新建一个节点类
2、把数据封装成节点,放到容器中,用于建立一个森林
3、循环寻找权值最小的两个节点,用于构造新的节点
需要定义一个方法,来寻找当前节点插入到森林中的位置
获取哈夫曼编码(用于后面文件的压缩与解压缩)
二、二叉树的构造源代码:
节点类:
package MyTree;
public class Node {
//节点类、
public int data;
public Node left;
public Node right;
}
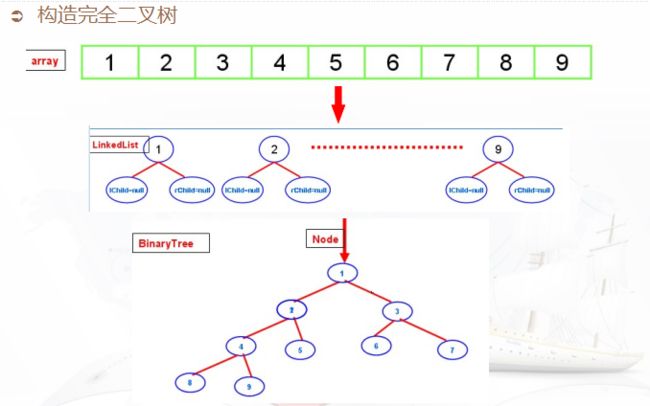
二叉树的构造过程以及遍历:
package MyTree;
import java.util.ArrayList;
public class TreeList {
public int [] values ={1,2,3,4,5,6,7,8,9};
public ArrayList list = new ArrayList();
public static void main(String[] args) {
TreeList tree = new TreeList();
Node root=tree.createTree();
System.out.println("前序遍历:");
tree.lookTree1(root);
System.out.println("中序遍历:");
tree.lookTree2(root);
System.out.println("后序遍历:");
tree.lookTree3(root);
}
public Node createTree(){
//封装成节点
for (int i = 0; i < values.length; i++) {
Node node = new Node();
node.data=values[i];
list.add(node);
}
//构造二叉树
for (int i = 0; i < list.size()/2-1; i++) {
Node node =list.get(i);
node.left=list.get(2*i+1);
node.right=list.get(2*i+2);
}
//构造最后一个父节点
Node lastNode = list.get(list.size()/2-1);
lastNode.left=list.get((list.size()/2-1)*2+1);
if(list.size()%2==1){
lastNode.right=list.get((list.size()/2-1)*2+2);
}
return list.get(0);
}
//前序遍历
public void lookTree1(Node root){
System.out.print(root.data+" ");
if(root.left!=null){
lookTree1(root.left);
}
if(root.right!=null){
lookTree1(root.right);
}
}
//中序遍历
public void lookTree2(Node root){
if(root.left!=null){
lookTree2(root.left);
}
System.out.print(root.data+" ");
if(root.right!=null){
lookTree2(root.right);
}
}
//后续遍历
public void lookTree3(Node root){
if(root.left!=null){
lookTree3(root.left);
}
if(root.right!=null){
lookTree3(root.right);
}
System.out.print(root.data+" ");
}
}
三、构造哈夫曼树的源代码:
哈夫曼节点类:
package com.bluesky.huffm;
public class HuffmNode {
//构造HuffmNode类
private int data;
private HuffmNode left;
private HuffmNode right;
//HuffmNode类构造函数
public HuffmNode(int data) {
this.data=data;
}
//封装属性
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public HuffmNode getLeft() {
return left;
}
public void setLeft(HuffmNode left) {
this.left = left;
}
public HuffmNode getRight() {
return right;
}
public void setRight(HuffmNode right) {
this.right = right;
}
}
package com.bluesky.huffm;
import java.util.LinkedList;
public class HuffmTree {
public int [] datas ={2,1,6,4,7,9,12,3};
public LinkedList list = new LinkedList();
public HuffmNode createTree() {
//按照从小到大的将数据封装成节点
for (int i = 0; i < datas.length; i++) {
HuffmNode node = new HuffmNode(datas[i]);
//得到需要插入的位置索引
int index=getIndex(node);
//将数据添加到容器中
list.add(index, node);
}
//构造哈夫曼树
while(list.size()>1){
//移除容器中的第一个节点
HuffmNode firstNode =list.removeFirst();
//容器中原来的第二个节点变成新的第一个节点
HuffmNode secondNode =list.removeFirst();
//构造父节点数据域
HuffmNode fatherNode = new HuffmNode(firstNode.getData()+secondNode.getData());
//构造父节点左子叶
fatherNode.setLeft(firstNode);
//构造父节点右子叶
fatherNode.setRight(secondNode);
//得到构造好的父节点的索引
int index=getIndex(fatherNode);
//将父节点加入森林
list.add(index, fatherNode);
}
//返回根节点
return list.getFirst();
}
//得到索引
public int getIndex(HuffmNode node) {
for (int i = 0; i < list.size(); i++) {
if(node.getData()>list.get(i).getData()){
continue;
}else {
return i;
}
}
//如果比容器中的任何一个数大,则插入最后面
return list.size();
}
//得到哈夫曼编码
public void getHuffmCode(HuffmNode root,String code) {
if(root.getLeft()!=null){
getHuffmCode(root.getLeft(),code+"0");
}
if(root.getRight()!=null){
getHuffmCode(root.getRight(),code+"1");
}
if(root.getLeft()==null && root.getRight()==null){
System.out.println(code);
}
}
}
程序入口:
package com.bluesky.huffm;
public class Test {
public static void main(String[] args) {
HuffmTree tree = new HuffmTree();
HuffmNode root = tree.createTree();
tree.getHuffmCode(root, "");
}
}
树是属于数据结构方面的知识,以前自己在学数据结构的时候,就被老师要求自己去构造一些诸如链表,队列等数据结构,并且要能够实现这些数据结构的增删查改等功能!链表和队列还算简单的了,树和图就真的有点蒙了,其实数据结构这门课程还是挺重要的了,这不,我们马上就要看到哈夫曼树的用处了;树的递归遍历真的有点难理解,都不知道递归到哪里去了;一直纠结就会陷入死循环,有时也不要那么纠结,你递归下去,脑袋立马蒙了,当然,有些逻辑非常清楚的人就不会,只能说,我还需要历练!
哈夫曼树,也称最优二叉树,是树型结构中比较重要的知识,以前只知道它大有用处,却不知到它该怎么用,现在算是见证到哈夫曼树的威力了!构造哈弗曼树的过程中,需要注意,移除子节点后,第二字节点就变成了第一个节点,这里需要注意下!
共勉!