Iris数据集的 Fisher线性分类以及数据可视化
这用Jupyter完成Iris数据集的 Fisher线性分类,并学习数据可视化技术 。
- 用Jupyter完成Iris数据集的 Fisher线性分类,并学习数据可视化技术 。
- 一、完成Iris数据集的 Fisher线性分类判断准确率
- 二、学习数据可视化
- 1、数据概览
- 1.1、读取文件
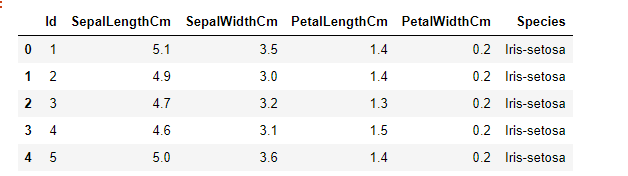
- 1.2、前五行数据
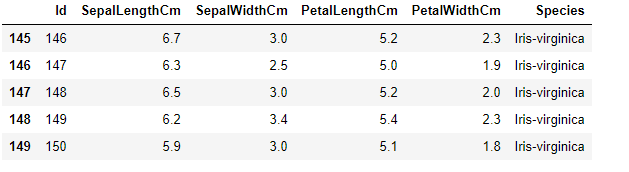
- 1.3、后五行数据
- 1.4、查看数据整体信息
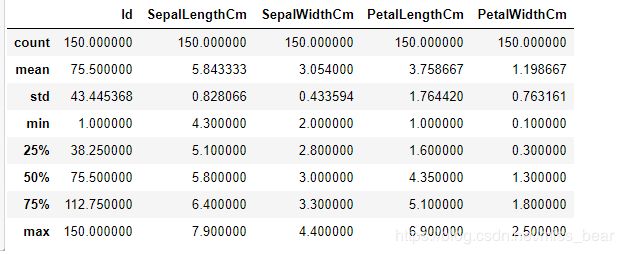
- 1.5、描述性统计
- 1.6、对每种特征计数
- 2、特征工程
- 2.1、引入可视化所需要的库
- 2.2、去掉Species下的字符
- 2.2、绘制花萼的长度与宽度的散点图
- 2.3、绘制花瓣的长度与宽度的散点图
- 2.4、Id编号与花萼长度, 花萼宽度, 花瓣长度, 花瓣宽度之间的关系
- 2.5、散点图与直方图的同时显示
- 2.6、绘制直方图
- 2.7、绘制箱线图
- 2.8、绘制琴图
- 2.9、绘制分布图
用Jupyter完成Iris数据集的 Fisher线性分类,并学习数据可视化技术 。
一、完成Iris数据集的 Fisher线性分类判断准确率
python代码如下所示:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
path=r'media/Iris.csv'
df = pd.read_csv(path, header=0)
Iris1=df.values[0:50,0:4]
Iris2=df.values[50:100,0:4]
Iris3=df.values[100:150,0:4]
m1=np.mean(Iris1,axis=0)
m2=np.mean(Iris2,axis=0)
m3=np.mean(Iris3,axis=0)
s1=np.zeros((4,4))
s2=np.zeros((4,4))
s3=np.zeros((4,4))
for i in range(0,30,1):
a=Iris1[i,:]-m1
a=np.array([a])
b=a.T
s1=s1+np.dot(b,a)
for i in range(0,30,1):
c=Iris2[i,:]-m2
c=np.array([c])
d=c.T
s2=s2+np.dot(d,c)
#s2=s2+np.dot((Iris2[i,:]-m2).T,(Iris2[i,:]-m2))
for i in range(0,30,1):
a=Iris3[i,:]-m3
a=np.array([a])
b=a.T
s3=s3+np.dot(b,a)
sw12=s1+s2
sw13=s1+s3
sw23=s2+s3
#投影方向
a=np.array([m1-m2])
sw12=np.array(sw12,dtype='float')
sw13=np.array(sw13,dtype='float')
sw23=np.array(sw23,dtype='float')
#判别函数以及T
#需要先将m1-m2转化成矩阵才能进行求其转置矩阵
a=m1-m2
a=np.array([a])
a=a.T
b=m1-m3
b=np.array([b])
b=b.T
c=m2-m3
c=np.array([c])
c=c.T
w12=(np.dot(np.linalg.inv(sw12),a)).T
w13=(np.dot(np.linalg.inv(sw13),b)).T
w23=(np.dot(np.linalg.inv(sw23),c)).T
#print(m1+m2) #1x4维度 invsw12 4x4维度 m1-m2 4x1维度
T12=-0.5*(np.dot(np.dot((m1+m2),np.linalg.inv(sw12)),a))
T13=-0.5*(np.dot(np.dot((m1+m3),np.linalg.inv(sw13)),b))
T23=-0.5*(np.dot(np.dot((m2+m3),np.linalg.inv(sw23)),c))
kind1=0
kind2=0
kind3=0
newiris1=[]
newiris2=[]
newiris3=[]
for i in range(30,49):
x=Iris1[i,:]
x=np.array([x])
g12=np.dot(w12,x.T)+T12
g13=np.dot(w13,x.T)+T13
g23=np.dot(w23,x.T)+T23
if g12>0 and g13>0:
newiris1.extend(x)
kind1=kind1+1
elif g12<0 and g23>0:
newiris2.extend(x)
elif g13<0 and g23<0 :
newiris3.extend(x)
#print(newiris1)
for i in range(30,49):
x=Iris2[i,:]
x=np.array([x])
g12=np.dot(w12,x.T)+T12
g13=np.dot(w13,x.T)+T13
g23=np.dot(w23,x.T)+T23
if g12>0 and g13>0:
newiris1.extend(x)
elif g12<0 and g23>0:
newiris2.extend(x)
kind2=kind2+1
elif g13<0 and g23<0 :
newiris3.extend(x)
for i in range(30,50):
x=Iris3[i,:]
x=np.array([x])
g12=np.dot(w12,x.T)+T12
g13=np.dot(w13,x.T)+T13
g23=np.dot(w23,x.T)+T23
if g12>0 and g13>0:
newiris1.extend(x)
elif g12<0 and g23>0:
newiris2.extend(x)
elif g13<0 and g23<0 :
newiris3.extend(x)
kind3=kind3+1
#花瓣与花萼的长度散点图
plt.scatter(df.values[:50, 3], df.values[:50, 1], color='red', marker='o', label='setosa')
plt.scatter(df.values[50:100, 3], df.values[50: 100, 1], color='blue', marker='x', label='versicolor')
plt.scatter(df.values[100:150, 3], df.values[100: 150, 1], color='green', label='virginica')
plt.xlabel('petal length')
plt.ylabel('sepal length')
plt.title("花瓣与花萼长度的散点图")
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签
plt.rcParams['axes.unicode_minus']=False
plt.legend(loc='upper left')
plt.show()
#花瓣与花萼的宽度度散点图
plt.scatter(df.values[:50, 4], df.values[:50, 2], color='red', marker='o', label='setosa')
plt.scatter(df.values[50:100, 4], df.values[50: 100, 2], color='blue', marker='x', label='versicolor')
plt.scatter(df.values[100:150, 4], df.values[100: 150, 2], color='green', label='virginica')
plt.xlabel('petal width')
plt.ylabel('sepal width')
plt.title("花瓣与花萼宽度的散点图")
plt.legend(loc='upper left')
plt.show()
correct=(kind1+kind2+kind3)/60
print("样本类内离散度矩阵S1:",s1,'\n')
print("样本类内离散度矩阵S2:",s2,'\n')
print("样本类内离散度矩阵S3:",s3,'\n')
print('-----------------------------------------------------------------------------------------------')
print("总体类内离散度矩阵Sw12:",sw12,'\n')
print("总体类内离散度矩阵Sw13:",sw13,'\n')
print("总体类内离散度矩阵Sw23:",sw23,'\n')
print('-----------------------------------------------------------------------------------------------')
print('判断出来的综合正确率:',correct*100,'%')
运行结果
二、学习数据可视化
1、数据概览
1.1、读取文件
import pandas as pd
df_Iris = pd.read_csv(r'media/Iris.csv')
1.2、前五行数据
#前五行数据
df_Iris.head()
1.3、后五行数据
#后五行数据
df_Iris.tail()
1.4、查看数据整体信息
#查看数据整体信息
df_Iris.info()
1.5、描述性统计
#描述性统计
df_Iris.describe()
1.6、对每种特征计数
df_Iris.Species.value_counts()
2、特征工程
2.1、引入可视化所需要的库
Seaborn是一个python的可视化库, 它基于matplotlib, 这使得它能与pandas紧密结合, 并且提供了高级绘图界面, 能更方便地完成探索性分析.
import seaborn as sns
import matplotlib.pyplot as plt
#sns初始化
sns.set()
2.2、去掉Species下的字符
df_Iris['Species']= df_Iris.Species.apply(lambda x: x.split('-')[1])
df_Iris.Species.unique()
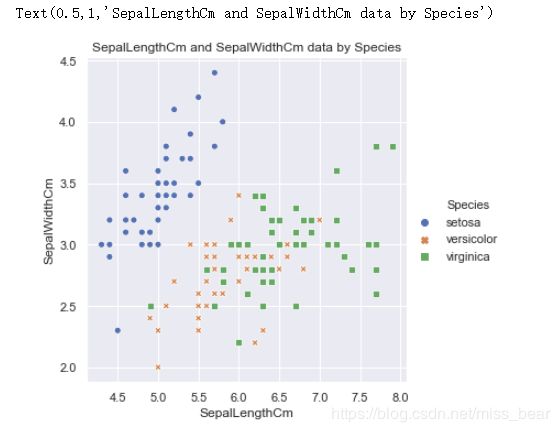
2.2、绘制花萼的长度与宽度的散点图
#花萼长度与宽度
sns.relplot(x='SepalLengthCm', y='SepalWidthCm', hue='Species', style='Species', data=df_Iris )
plt.title('SepalLengthCm and SepalWidthCm data by Species')
2.3、绘制花瓣的长度与宽度的散点图
#花瓣长度与宽度散点分布图
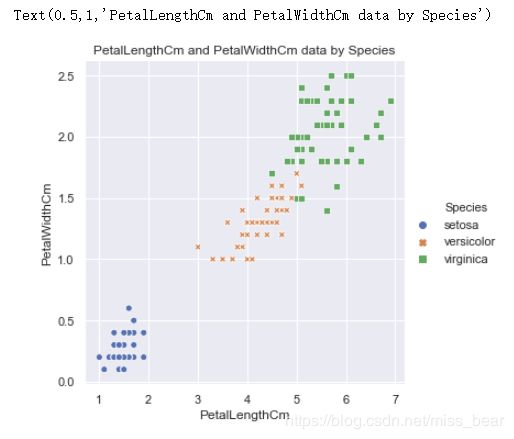
sns.relplot(x='PetalLengthCm', y='PetalWidthCm', hue='Species', style='Species', data=df_Iris )
plt.title('PetalLengthCm and PetalWidthCm data by Species')
2.4、Id编号与花萼长度, 花萼宽度, 花瓣长度, 花瓣宽度之间的关系
#花萼长度与Id之间关系图
sns.relplot(x="Id", y="SepalLengthCm",hue="Species", style="Species",kind="line", data=df_Iris)
plt.title('SepalLengthCm and Id data analysize')
#花萼宽度与Id之间关系图
sns.relplot(x="Id", y="SepalWidthCm",hue="Species", style="Species",kind="line", data=df_Iris)
plt.title('SepalWidthCm and Id data analysize')
#花瓣长度与Id之间关系图
sns.relplot(x="Id", y="PetalLengthCm",hue="Species", style="Species",kind="line", data=df_Iris)
plt.title('PetalLengthCm and Id data analysize')
#花瓣宽度与Id之间关系图
sns.relplot(x="Id", y="PetalWidthCm",hue="Species", style="Species",kind="line", data=df_Iris)
plt.title('PetalWidthCm and Id data analysize')
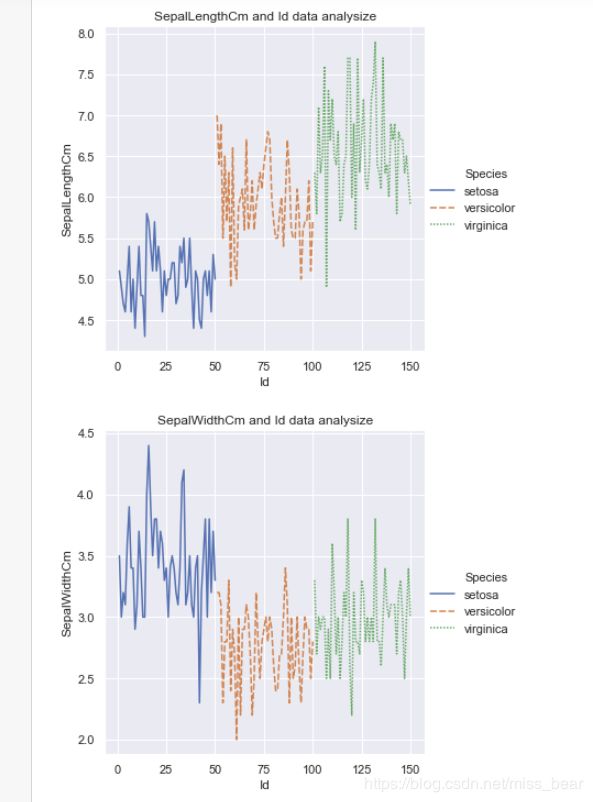
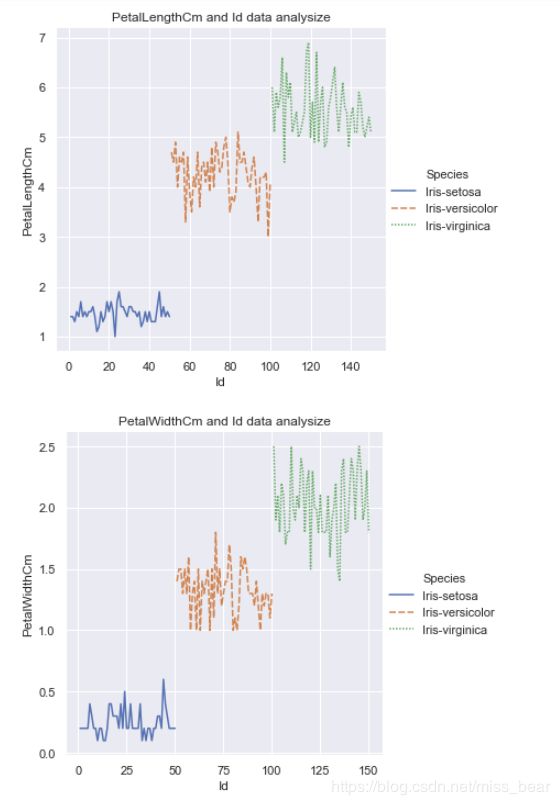
根据这个可以得到信息: Id中前50个为setosa, 51到100为versicolour, 101到150为Virginica, 以及每个种类对应属性值的范围,与CSV文件中的分布一致。
2.5、散点图与直方图的同时显示
直方图可以比较直观的看出频数的大小
#花萼长度与宽度直方图
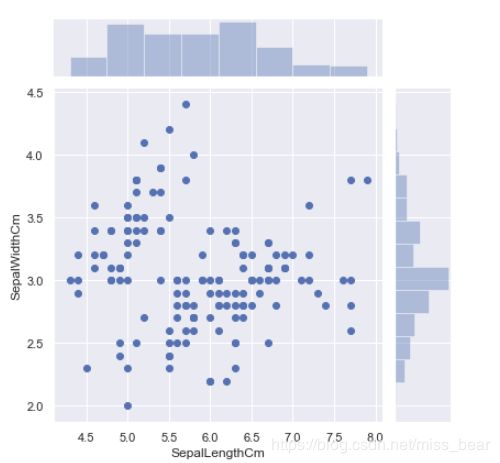
sns.jointplot(x='SepalLengthCm', y='SepalWidthCm', data=df_Iris)
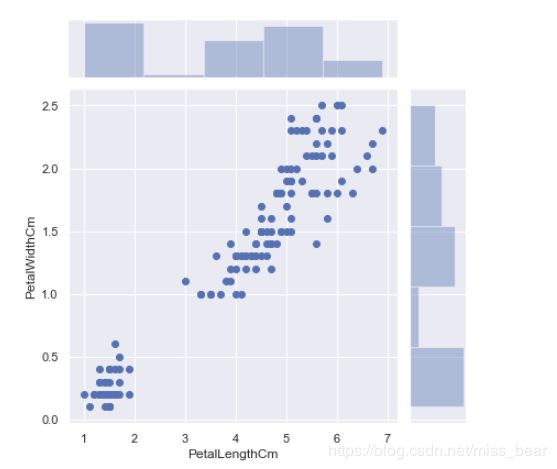
#花瓣长度与宽度直方图
sns.jointplot(x='PetalLengthCm', y='PetalWidthCm', data=df_Iris)
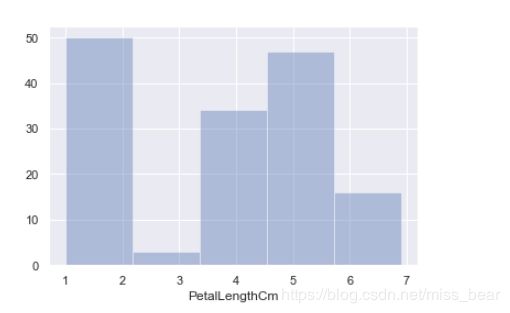
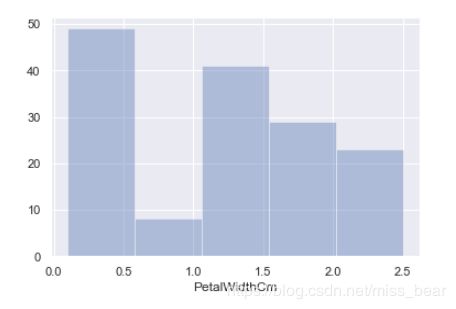
2.6、绘制直方图
#绘制直方图, 其中kde=False表示不显示核函数估计图,这里为了更方便去查看频数而设置它为False.
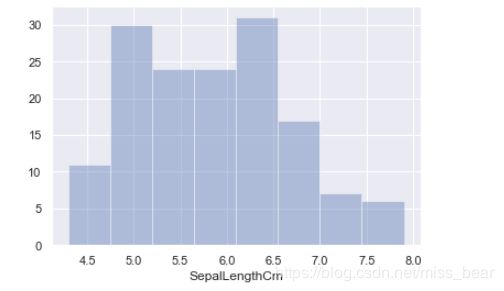
sns.distplot(df_Iris.SepalLengthCm,bins=8, hist=True, kde=False)
sns.distplot(df_Iris.SepalWidthCm,bins=13, hist=True, kde=False)
sns.distplot(df_Iris.PetalLengthCm, bins=5, hist=True, kde=False)
sns.distplot(df_Iris.PetalWidthCm, bins=5, hist=True, kde=False)
2.7、绘制箱线图
箱线图能显示出一组数据的最大值, 最小值, 四分位数以及异常点.
#比如数据中的SepalLengthCm属性
sns.boxplot(x='SepalLengthCm', data=df_Iris)

为了更直观地对比四个属性之间的关系, 将四个属性对应的数值合并在新的DataFrame Iris中.
#对于每个属性的data创建一个新的DataFrame
Iris1 = pd.DataFrame({"Id": np.arange(1,151), 'Attribute': 'SepalLengthCm', 'Data':df_Iris.SepalLengthCm, 'Species':df_Iris.Species})
Iris2 = pd.DataFrame({"Id": np.arange(151,301), 'Attribute': 'SepalWidthCm', 'Data':df_Iris.SepalWidthCm, 'Species':df_Iris.Species})
Iris3 = pd.DataFrame({"Id": np.arange(301,451), 'Attribute': 'PetalLengthCm', 'Data':df_Iris.PetalLengthCm, 'Species':df_Iris.Species})
Iris4 = pd.DataFrame({"Id": np.arange(451,601), 'Attribute': 'PetalWidthCm', 'Data':df_Iris.PetalWidthCm, 'Species':df_Iris.Species})
#将四个DataFrame合并为一个.
Iris = pd.concat([Iris1, Iris2, Iris3, Iris4])
#绘制箱线图
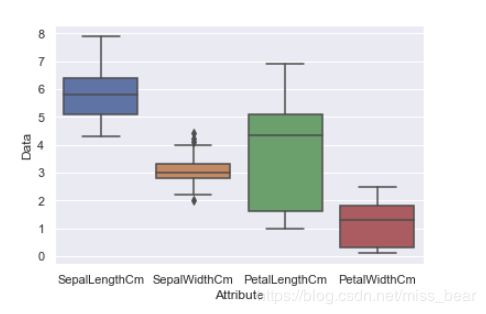
sns.boxplot(x='Attribute', y='Data', data=Iris)
对于下图: 就中位数来说, SepalLenthCm > PetalLengthCm > SepalWidthCm > PetalWidthCm; 就波动程度来说, PetalLengthCm > PetalWidthCm > SepalLengthCm > SepalWidthCm; 就异常值来说, 只有SepalWidthCm中存在异常值.
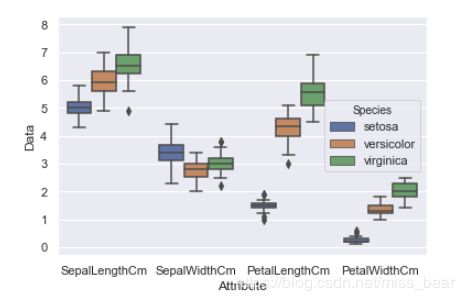
将鸢尾花的三种种类再加入到箱线图中:
sns.boxplot(x='Attribute', y='Data',hue='Species', data=Iris)
2.8、绘制琴图
是箱线图与核密度图的结合体, 既可以展示四分位数, 又可以展示任意位置的密度.
sns.violinplot(x='Attribute', y='Data', hue='Species', data=Iris )
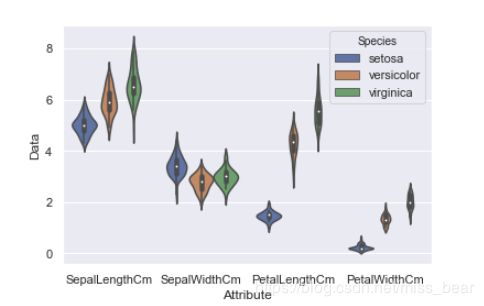
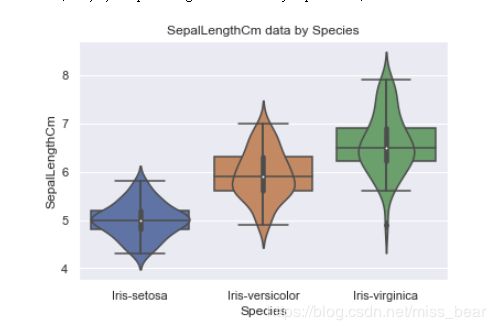
可将上面一张图片拆个成四个小图片,这样可以看出一些具体的细节
#花萼长度
# sns.boxplot(x='Species', y='SepalLengthCm', data=df_Iris)
# sns.violinplot(x='Species', y='SepalLengthCm', data=df_Iris)
# plt.title('SepalLengthCm data by Species')
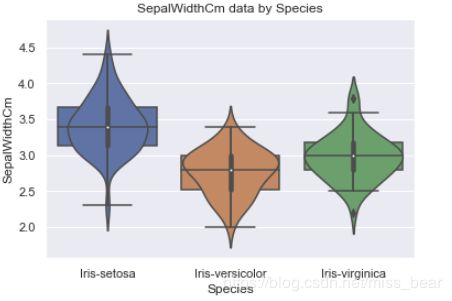
#花萼宽度
# sns.boxplot(x='Species', y='SepalWidthCm', data=df_Iris)
# sns.violinplot(x='Species', y='SepalWidthCm', data=df_Iris)
# plt.title('SepalWidthCm data by Species')
#花瓣长度
# sns.boxplot(x='Species', y='PetalLengthCm', data=df_Iris)
# sns.violinplot(x='Species', y='PetalLengthCm', data=df_Iris)
# plt.title('PetalLengthCm data by Species')
#花瓣宽度
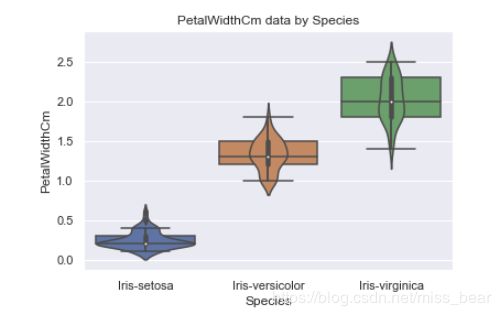
sns.boxplot(x='Species', y='PetalWidthCm', data=df_Iris)
sns.violinplot(x='Species', y='PetalWidthCm', data=df_Iris)
plt.title('PetalWidthCm data by Species')
2.9、绘制分布图
sns.pairplot(df_Iris.drop('Id', axis=1), hue='Species')
#保存图片, 由于在jupyter notebook中太大, 不能一次截图
plt.savefig('pairplot.png')
plt.show()

综上可知,花萼的长度, 花萼的宽度, 花瓣的长度, 花瓣的宽度与花的种类之间均存在一定的相关性, 且对于这三个种类的分布, satosa在任何一种分布中较其他两者集中; 就同一种花的平均水平来看, 其花萼的长度最长, 花瓣的宽度最短; 就同一属性的平均水平来看, 三种花在除了花萼的宽度外的属性中平均水平均表现为: Virginica > versicolour > setosa.