聚类算法 之 K-means算法和手写代码

聚类算法为无监督学习算法，用处很多，比如图像检测中边框回归，往往会对图片的宽和高进行聚类，找到几个比较典型anchor，然后再通过边框回归设定权重，求出目标图像和anchor的宽高的比值。
聚类算法种类很多，主流的有基于划分、基于层次、基于密度、基于网络的。其中K-means聚类算法就是基于划分的，这个很好理解，目标是找到几个相同类型的数据的中心点，然后把离这几个中心点最近的划分成一类。判断标准也很好理解，就是数据离某个中心点的距离比里其他的中心点距离都小，就聚集在这个中心点周围。

1.基本原理

K-means中“K”就是要分成K个类，“mean”表示这个中心点的计算是通过将某些可能是一类的数据求平均，计算得到中心点，“s”表示有多个这样的平均值。
算法流程大概是这样的：
①确定将数据分成几类，就是定下K的值
②确定K个初始中心点，用于将数据围绕这几个中心点进行汇聚
③计算每个数据到中心点的距离，离哪个最近就划分给谁
④计算每个划分好的数据类的均值点，也就是每个维度求平均，定一个新的中心点
⑤重负③④步骤，直到完成指定次数或者达到某个终止条件。

2.代码

看了很多介绍，不如自己写一个K-means，Python的数据结构和c或者c++很不一样，这里主要用array存储数据，数据处理的时候有两个小坑：
一是建立array的结构以后，使用append或者concatenate的时候一定注意是哪一层的数据进行了组合，否则数据结构和索引会乱
二是浅拷贝和深拷贝，两个array使用“=”赋值后，实际上是进行了指针的复制，这里使用的解决办法是采用

y = [x for in array]

的方式实现真正意义的浅拷贝，这个代码结构相当于

for x in array:
    y.append(x)

这样无论如何修改array，y的值都不会变化
如果使用

x =  array

令x作为暂存的中间变量，x将起不到暂存作用，x中元素的内容将跟着array联动
下面是一个基本的演示代码：

import numpy as np
import os
import matplotlib.pyplot as plt

#返回array的均值点，如果arr中为多维，将对每个维度求平均，最后确定一个均值点
def mean(arr):
    arr_mean = []
    if arr.__len__() == 0:
        return 0
    for i in range(arr[0].__len__()):
        arr_mean.append(np.mean([e[i] for e in arr]))
    return arr_mean

#返回点e和点集arr中每个点的距离
def distance(e,arr):
    dsum = 0
    for a in arr:
        for i in range(arr[0].__len__()):
            dsum += pow((a[i] - e[i]),2)
    d = np.sqrt(dsum)
    return d

#返回点集arr1和点集arr2的距离
def distance2(arr1,arr2):
    if arr1.__len__() != arr2.__len__():
        return -1

    if arr1.__len__() == 0:
        return 0

    dsum = 0
    for i in range(arr1.__len__()):
        dsuma = 0
        for j in range(arr1[0].__len__()):
            dsuma += pow((arr1[i][j] - arr2[i][j]),2)
        dsum += dsuma
    d = np.sqrt(dsum)
    return d

#返回arr点集中，距离k_arr最远的点及索引的集合，用于求离散度最大的点
#输入的是两个array，输出的是一个array，引用的时候注意层次
def farthest(k_arr,arr):
    ae_max = []
    arrindex = []
    for k_e in k_arr:
        d_max = 0
        for i in range(arr.__len__()):
            d = distance(k_e,(list)([arr[i]])) 
            if d >= d_max:
                d_max = d
                f_e = arr[i]
                index = i
        ae_max.append(f_e)
        arrindex.append(index)
    return ae_max,arrindex

#返回arr点集中，距离k_arr最近的点及索引的集合，用于求距离中心点最近的点集
def closest(k_arr,arr):
    ae_min = []
    arrindex = []
    for k_e in k_arr:
        d_min = distance(k_e,(list)([arr[0]]))
        for i in range(arr.__len__()):
            d = distance(k_e,(list)([arr[i]]))           
            if d <= d_min:
                d_min = d
                c_e = arr[i]
                index = i
        ae_min.append(c_e)
        arrindex.append(index)
    return ae_min,arrindex

#生成K个初始点和存储聚类点的容器
#计算初始中心时，确定第一个点后，为了避免在两个点之间循环往复，每次求出一个点，下次将这个点剔出备选点集合
#为了避免找到的初始点过偏，最新的初始中心点为前两个点的平均位置的最远点
def init_center(K,arr):
    r = np.random.randint(arr.__len__())
    cen = []
    cen_f = []
    container = []
    for i in range(K):
        if i == 0:
            cen.append(arr[r])
            cen_f.append(arr[r])
            arr = np.delete(arr,arr[r],axis=0)
        else:
            fa,ind = farthest(cen,arr)
            cen_f.append(fa[0])
            cen_mean = mean(fa)
            clo,ind_c = closest([cen_mean],arr)
            cen.append(clo[0])
            arr = np.delete(arr,clo[0],axis=0)
        container.append([])
    return cen, container

#返回一个中心点集合对应的全体数据的聚类
def cluster_each_element(k_arr,arr,containers):
    container = containers.copy()
    for e in arr:
        clo_k,ind = closest([e],k_arr)        
        container[ind[0]].append(e)                       

    return container

#返回均值法计算的新的中心点位置
def adjust_center(cluster_container):
    adjusted = []
    for c in cluster_container:
        meaneach = mean(c)
        adjusted.append(meaneach)
    return adjusted

#返回最终的聚类结果即收敛趋势
def cluster_all_element(K,elements,itertimes,errorth = 0.01):
    mean = []
    errortrend = []
    errorind = []
    K_arr, container = init_center(K,elements)
    for i in range(itertimes):
        container = [[] for i in range(K)]
        K_last = [i for i in K_arr]
        outcon = cluster_each_element(K_arr,elements,container)
        if i != (itertimes-1):
            K_arr = adjust_center(outcon)
            errordist = distance2(K_last,K_arr)
            print(errordist)      
        '''
        if errordist < errorth:
            print('error is small enough')
            break
        '''  
        errortrend.append(errordist)
        errorind.append(i)
    
    return K_arr, outcon, errorind, errortrend


if __name__ == '__main__':
    
    K = 3
    colorCON = ['Chartreuse','yellow','Aqua']
    arr1 = np.random.randint(30, size=(10,1,2))[:,0,:]
    arr2 = np.random.randint(30, 50, size=(40,1,2))[:,0,:]
    arr3 = np.random.randint(40, 90, size=(20,1,2))[:,0,:]
    arr = np.concatenate((arr1,arr2,arr3))
    
    mean, out, ind, trend = cluster_all_element(3,arr,30)
    
    plt.figure(1)
    for i in range(K):
        for e in out[i]:
            plt.scatter(e[0],e[1],color=colorCON[i])
    for e in mean:
        plt.scatter(e[0],e[1],color='blue')
    
    plt.figure(2)
    plt.plot(ind,trend)
    plt.show()

3.实验结果

设定3簇数据点，使用K=3进行聚类分析，结果如图：

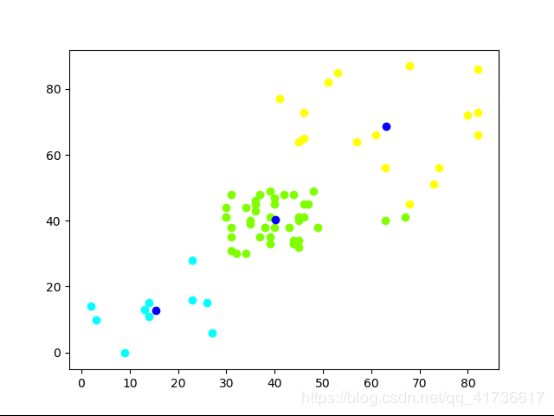
收敛趋势如图，横轴为迭代次数，纵轴为当前中心点和上迭代中心点距离。基本上迭代次数3到8次即可收敛