WaWa的奇妙冒险（第一周集训自闭现场）

（一）例题记录

A-Download Manager （水题） HDU - 3233

    Jiajia downloads a lot, a lot more than you can even imagine. Some say that he starts downloading up to 20,000 files together. If 20,000 files try to share a limited bandwidth then it will be a big hazard and no files will be downloaded properly. That is why, he uses a download manager.

    If there are T files to download, the download manger uses the following policy while downloading files:

1. The download manager gives the smaller files higher priority, so it starts downloading the smallest n files at startup. If there is a tie, download manager chooses the one with less bytes remaining (for download). We assume that with at least 50 Mega Bytes/sec of bandwidth, n files can be downloaded simultaneously without any problem.

2. The available bandwidth is equally shared by the all the files that are being downloaded. When a file is completely downloaded its bandwidth is instantaneously given to the next file. If there are no more files left except the files that are being downloaded, this bandwidth is immediately shared equally by all remaining files that are being downloaded.

    Given the size and completed percentage of each file, your task is to intelligently simulate the behavior of the download manager to find the total time required to download all the files.

Input

    The will be at most 10 test cases. Each case begins with three integers T (1 <= T <= 20000), n (1 <= n <= 2000 and 1 <= n <= T) and B (50 <= B <= 1000). Here B denotes the total bandwidth available to Jiajia (In Megabytes/sec). Please note that the download manager always downloads n files in parallel unless there are less than n files available for download. Each of next T lines contains one non-negative floating-point number S (less than 20,000, containing at most 2 digits after the decimal places) and one integer P (0 <= P <= 100). These two numbers denote a file whose size is S megabyte and which has been downloaded exactly P% already. Also note that although theoretically it is not possible that the size of a file or size of its remaining part is a fraction when expressed in bytes, for simplicity please assume that such thing is possible in this problem. The last test case is followed by T=n=B=0, which should not be processed.

Output

    For each case, print the case number and the total time required to download all the files, expressed in hours and rounded to 2 digits after the decimal point. Print a blank line after the output of each test case.

Sample Input

6 3 90
100.00 90
40.40 70
60.30 70
40.40 80
40.40 85
40.40 88
1 1 56
12.34 100
0 0 0

Sample Output

Case 1: 0.66

Case 2: 0.00

理解

	题目强调了同时下载的任务上限和下载速度上限（这里的下载速度会平均分配给所有的正在下载的任务）
	所以“同一时间段的的下载任务上限”其实是一个无用信息
	只需要算出还需下载的任务量除以下载速度即可得到答案

AC代码

#include 
using namespace std;

int main()
{
	int t,n,b,s = 0;
	while(~scanf("%d %d %d",&t,&n,&b)){
		if(!t && !n && !b) break;
		double p,sum = 0;
		int k;
		while(t--){
			cin >> p >> k;
			sum += p*(1 - k/100.00);
		}
		s++;
		printf("Case %d: ",s);
		printf("%.2f\n\n",sum/(double)b);
	}
	return 0;
}

B-Joseph（打表题） POJ - 1012

    The Joseph’s problem is notoriously known. For those who are not familiar with the original problem: from among n people, numbered 1, 2, . . ., n, standing in circle every mth is going to be executed and only the life of the last remaining person will be saved. Joseph was smart enough to choose the position of the last remaining person, thus saving his life to give us the message about the incident. For example when n = 6 and m = 5 then the people will be executed in the order 5, 4, 6, 2, 3 and 1 will be saved.

    Suppose that there are k good guys and k bad guys. In the circle the first k are good guys and the last k bad guys. You have to determine such minimal m that all the bad guys will be executed before the first good guy.

Input

    The input file consists of separate lines containing k. The last line in the input file contains 0. You can suppose that 0 < k < 14.

Output

    The output file will consist of separate lines containing m corresponding to k in the input file.

Sample Input

3
4
0

Sample Output

5
30

理解

	神奇的打表题，可以无限循环找出m，但需要时间太久，偷鸡去网上找了约瑟夫环的递推公式
	找出m的方式，确认剩余人数只有一半的时候，是否出局的人都是后k个人，一个while循环即可

AC代码

约瑟夫环递推公式
f[n] = (f[n-1] + m)%n //m表示每次数到该数的人出列，n表示当前序列的总人数。

#include 
#include 
using namespace std;
int a[15] = {0},k;

##  判断该m（x）是否能确定在保留好人的情况下踢出所有坏人
int jsk(int x,int y){
	int s = 0,n = y*2;
	while(n > y){
		s = (s + x - 1) % n; ##  因为第一个人编号为0，自己喊算一次
		if(s < y) return 0;
		n--;
	}
	return 1;
}

##  打表，确实k为1到14时，最小的能保留所有好人的m
void ss(){
	for(int i = 1;i <= 14;i++){
		for(int j = 1;;j++){
			if(jsk(j,i)){
				a[i] = j;
				break;
			}
		}
	}
}

int main()
{
	ss();
	while(~scanf("%d",&k)){
    	if(!k) break;
    	cout << a[k] << endl; 
	}
	return 0;
}

C-Master-Mind Hints （模拟题） UVA - 340

    MasterMind is a game for two players. One of them, Designer, selects a secret code. The other, Breaker,tries to break it. A code is no more than a row of colored dots. At the beginning of a game, the players agree upon the length N that a code must have and upon the colors that may occur in a code.
    In order to break the code, Breaker makes a number of guesses, each guess itself being a code. After each guess Designer gives a hint, stating to what extent the guess matches his secret code.
    In this problem you will be given a secret code s1 . . . sn and a guess g1 . . . gn, and are to determine the hint. A hint consists of a pair of numbers determined as follows.
    A match is a pair (i, j), 1 ≤ i ≤ n and 1 ≤ j ≤ n, such that si = gj . Match (i, j) is called strong when i = j, and is called weak otherwise. Two matches (i, j) and (p, q) are called independent when i = p if and only if j = q. A set of matches is called independent when all of its members are pairwise independent.
    Designer chooses an independent set M of matches for which the total number of matches and the number of strong matches are both maximal. The hint then consists of the number of strong followed by the number of weak matches in M. Note that these numbers are uniquely determined by the secret code and the guess. If the hint turns out to be (n, 0), then the guess is identical to the secret code.

Input

    The input will consist of data for a number of games. The input for each game begins with an integer specifying N (the length of the code). Following these will be the secret code, represented as N integers,which we will limit to the range 1 to 9. There will then follow an arbitrary number of guesses, each also represented as N integers, each in the range 1 to 9. Following the last guess in each game will be N zeroes; these zeroes are not to be considered as a guess.
    Following the data for the first game will appear data for the second game (if any) beginning with a new value for N. The last game in the input will be followed by a single ‘0’ (when a value for N would normally be specified). The maximum value for N will be 1000.

Output

    The output for each game should list the hints that would be generated for each guess, in order, one hint per line. Each hint should be represented as a pair of integers enclosed in parentheses and separated by a comma. The entire list of hints for each game should be prefixed by a heading indicating the game number; games are numbered sequentially starting with 1. Look at the samples below for the exact format.

Sample Input

4
1 3 5 5
1 1 2 3
4 3 3 5
6 5 5 1
6 1 3 5
1 3 5 5
0 0 0 0
10
1 2 2 2 4 5 6 6 6 9
1 2 3 4 5 6 7 8 9 1
1 1 2 2 3 3 4 4 5 5
1 2 1 3 1 5 1 6 1 9
1 2 2 5 5 5 6 6 6 7
0 0 0 0 0 0 0 0 0 0
0

Sample Output

Game 1:
(1,1)
(2,0)
(1,2)
(1,2)
(4,0)
Game 2:
(2,4)
(3,2)
(5,0)
(7,0)

理解

	猜字谜的游戏，统计出A（位置和数字都对的sum），B（数字对但位置不对的sum）。
		这里可以看出优先统计A，然后统计B（可以看做一个连连看的思路）。
		通过建立x，y两个数组来确定某位置上的数字是否已经得到了匹配（可以看做连连看是否已经被消掉）。

AC代码

#include 
using namespace std;

int main()
{
	int a[1000],b[1000],s = 0,n; ##  a,b数组用于存储数据
	while(~scanf("%d",&n) && n){
		cout << "Game " << ++s << ":" << endl;
		for(int i = 0;i < n;i++){
			cin >> a[i];
		}
		int sa,sb;
		int x[1000],y[1000]; ## x,y数组用于查看该位置的数字是否已有配对
		while(1){
			sa = sb = 0;
			for(int j = 0;j < n;j++){
				cin >> b[j];
			}
			if(!b[0]) break;
				
			memset(x,0,sizeof(x));  ##  将所有位置标记为0,0表示该位置还没有被匹配
			memset(y,0,sizeof(y));
				
			for(int j = 0;j < n;j++){  ##  优先考虑A情况，找到位置和数字都对的位置，并标记为已经匹配
				if(a[j] == b[j]){
					sa++;
					x[j] = y[j] = 1;
				}
			}
				
			for(int j = 0;j < n;j++){  ##  枚举a，b所有可能的匹配样例
				for(int z = 0;z < n;z++){
					if(a[j] == b[z] && j != z && !x[j] && !y[z]){  ##  如果数字相等，且该两个位置都还没匹配，则说明这两个数位置不同但值相同，标记为匹配，并且使b + 1
						sb++;
						x[j] = 1;
						y[z] = 1;
					}
				}
			}
				
			cout << "    (" << sa << "," << sb << ")" << endl;
		}
	}
	return 0;
}

D-Digit Generator （反向打表） UVA - 1583

    For a positive integer N, the digit-sum of N is defined as the sum of N itself and its digits. When M is the digitsum of N, we call N a generator of M.
    For example, the digit-sum of 245 is 256 (= 245 + 2 + 4 + 5). Therefore, 245 is a generator of 256.
    Not surprisingly, some numbers do not have any generators and some numbers have more than one generator. For example, the generators of 216 are 198 and 207.You are to write a program to find the smallest generator of the given integer

Input

    Your program is to read from standard input. The input consists of T test cases. The number of test cases T is given in the first line of the input. Each test case takes one line containing an integer N,1 ≤ N ≤ 100, 000.

Output

    Your program is to write to standard output. Print exactly one line for each test case. The line is to contain a generator of N for each test case. If N has multiple generators, print the smallest. If N does not have any generators, print ‘0’.

Sample Input

3
216
121
2005

Sample Output

198
0
1979

理解

	这题要求找出最小的数，且该数字加上其各位的值能等于输入的值。
		挨个枚举极有可能会tle，所以使用一个反向思路，把1到100000与其自身各位数相加的值打成一个表。
		只要从1循环到输入的值中找不到能达到要求的数字，就可以判定无解，否则输出能找到的最小值。

AC代码

#include 
using namespace std;
int a[100005] = {0};
##  db == 打表，按思路反向打一个下标为“需要求的的答案”，值为“输入值”的表
void db(){
	a[1] = 0;
	for(int i = 1;i <= 100000;i++){
		a[i] = i;
		int j = i;
		while(j){  ##  加上这个数字各位的数
			a[i] = a[i] + j%10;
			j /= 10;
		}
	}
}

int main()
{
	db();
	int t;
	cin >> t;
	while(t--){
		int x,i;
		cin >> x;
		for(i = 1;i < x;i++){  ##  只用枚举到小于“输入值”即可，因为从等于“输入值”开始，就不可能找到要求的数字了
			if(a[i] == x){
				cout << i << endl;
				break;
			}
		}
		if(i == x) cout << 0 << endl;  ##  i == x则没找到，输出0即可
	}
	return 0;
}

E-Periodic Strings （周期性字符串） UVA - 455

    A character string is said to have period k if it can be formed by concatenating one or more repetitions of another string of length k. For example, the string ”abcabcabcabc” has period 3, since it is formed by 4 repetitions of the string ”abc”. It also has periods 6 (two repetitions of ”abcabc”) and 12 (one repetition of ”abcabcabcabc”).
    Write a program to read a character string and determine its smallest period.

Input

    The first line oif the input file will contain a single integer N indicating how many test case that your program will test followed by a blank line. Each test case will contain a single character string of up to 80 non-blank characters. Two consecutive input will separated by a blank line.

Output

    An integer denoting the smallest period of the input string for each input. Two consecutive output are separated by a blank line.

Sample Input

1
HoHoHo

Sample Output

2

理解

	这题难度不大，只要找出周期的子串就好了。
	记录这道题的原因是这道题的取模运算让我印象深刻，运用的非常巧妙。
	这题只要先找到长度能被字符串长度整除的串，然后判断是否能循环组成原字符串即可。

AC代码

#include 
using namespace std;
string s;
## 一个判断函数，判断这个子串能否组成原字符串
bool ss(int b,int l){
	if(l % (b + 1) != 0) return false;  ## 判断子串的长度能否被原串长度整除，如果不行则必不可嫩重新组成原串
	for(int j = b;j < l;j++){
		if(s[j % (b + 1)] != s[j]){  ## 用j % （b + 1）来找到子串中的对应位置，如果不同，则该子串是错误的，直接返回0
			return false;
		}
	}
	return true;
}

int main()
{
	int t;
	cin >> t;
	while(t--){
		cin >> s;
		int l = s.size(),k = 0;
		for(int i = 0;i < l;i++){
			if(ss(i,l)){  ## 遍历所有的子串，如果找到了对的子串，标记其尾部在原字符串中的下标（其加1即可得子串长度）
				k = i;
				break;
			}
		}
		cout << k + 1 << endl;
		if(t != 0) cout << endl;
	}
	return 0;
}

F-Repeating Decimals （余数的巧妙运用） UVA - 202

    The decimal expansion of the fraction 1/33 is 0.03, where the 03 is used to indicate that the cycle 03 repeats indefinitely with no intervening digits. In fact, the decimal expansion of every rational number (fraction) has a repeating cycle as opposed to decimal expansions of irrational numbers, which have no such repeating cycles.
    Examples of decimal expansions of rational numbers and their repeating cycles are shown below.Here, we use parentheses to enclose the repeating cycle rather than place a bar over the cycle.fraction decimal expansion repeating cycle cycle length

    Write a program that reads numerators and denominators of fractions and determines their repeating cycles.
    For the purposes of this problem, define a repeating cycle of a fraction to be the first minimal length string of digits to the right of the decimal that repeats indefinitely with no intervening digits. Thus for example, the repeating cycle of the fraction 1/250 is 0, which begins at position 4 (as opposed to 0 which begins at positions 1 or 2 and as opposed to 00 which begins at positions 1 or 4).

Input

    The first line oif the input file will contain a single integer N indicating how many test case that your program will test followed by a blank line. Each test case will contain a single character string of up to 80 non-blank characters. Two consecutive input will separated by a blank line.

Output

    An integer denoting the smallest period of the input string for each input. Two consecutive output are separated by a blank line.

Sample Input

1
HoHoHo

Sample Output

2

理解

	这道题的关键是想明白余数相同的时候就会开始循环，所以余数开始相同的时候就会出现循环节的结束点。
	所以我们可以写一个当余数相同时就停止的循环，然后从循环节开始的地方输出到尾部为止。
	值得一提的是，其中对于该余数是否出现过的数组的使用，刚开始我只是用0和1表示是否停止，无法正确输出循环节的长度，而网上大佬用当前长度。
	代替1的神奇做法十分巧妙，借着这种方法成功ac！（感谢大佬）

AC代码

#include 
using namespace std;
int x[1000000],y[1000000];  ##  用x数组存商，用y数组标记该余数是否已经出现，并且记录当前商的长度

int main()
{
	
	int a,b;
	while(~scanf("%d %d",&a,&b)){
		memset(x,0,sizeof(x));  ##  两个重置为0的操作，因为是多组样例输入
		memset(y,0,sizeof(y));
		cout << a << '/' << b << " = ";	
		
		int cnt = 1;
		x[0] = a / b;  ##  先算出整数部分，并存入x[0]中，因为整数部分对我们后面寻找循环节没有影响
		cout << x[0] << '.';
		
		a %= b;
		while(!y[a]){
			y[a] = cnt;  ##  y数组中的值不仅仅是作为该余数是否已经出现过的判断，也起了记录循环节起点和结尾的作用
			a *= 10;
			x[cnt++] = a / b;  ## 存入商
			a %= b;
		}
		
		int g;
		for(int i = 1;i < y[a];i++) cout << x[i];  ## 输出循环节前的所有商
		cout << '(';
		for(g = y[a];g < cnt && g <= 50;g++) cout << x[g];  ## 输出循环节
		if(g > 50 && cnt > 51) cout << "...)" << endl;  ## 多加一个cnt > 51的判断是为了防止出现正好输出了50个值时是循环节的结尾有加上了“...”
		else cout << ')' << endl;
		cout << "   " << cnt - y[a] << " = number of digits in repeating cycle" << endl << endl;
	}
	return 0;
}

G-Circular Sequence （模拟题） UVA - 1584

    Some DNA sequences exist in circular forms as in the following figure, which shows a circular sequence “CGAGTCAGCT”, that is, the last symbol “T” in “CGAGTCAGCT” is connected to the first symbol “C”. We always read a circular sequence in the clockwise direction.
    Since it is not easy to store a circular sequence in a computer as it is, we decided to store it as a linear sequence.However, there can be many linear sequences that are obtained from a circular sequence by cutting any place of the circular sequence. Hence, we also decided to store the linear sequence that is lexicographically smallest among all linear sequences that can be obtained from a circular sequence.
    Your task is to find the lexicographically smallest sequence from a given circular sequence. For the example in the figure,the lexicographically smallest sequence is “AGCTCGAGTC”. If there are two or more linear sequences that are lexicographically smallest, you are to find any one of them (in fact, they are the same).

Input

    The input consists of T test cases. The number of test cases T is given on the first line of the input file. Each test case takes one line containing a circular sequence that is written as an arbitrary linear sequence. Since the circular sequences are DNA sequences, only four symbols, ‘A’, ‘C’, ‘G’ and ‘T’, are allowed. Each sequence has length at least 2 and at most 100.

Output

    Print exactly one line for each test case. The line is to contain the lexicographically smallest sequence for the test case.

Sample Input

2
CGAGTCAGCT
CTCC

Sample Output

AGCTCGAGTC
CCCT

理解

	这道题要求你从一圈环状的字母中，找到字典循序最小的读法，并将其输出。
	实际上，我们只需要模拟头部字典循序最小的情况下的几种选择里最小的串就好了。
	因为不想用cpy和cmp等函数（其实是对c++里面封装的字符串函数不熟悉，不会用），我用改变下标的方式完成了模拟。

AC代码

#include 
using namespace std;

int main()
{
	int t;
	cin >> t;
	while(t--){
		char a[105];
		cin >> a;
		getchar();
		int l = strlen(a);  ##  将a字符串的长度赋值给l，因为要多次使用
		
		int min = 'Z';
		for(int i = 0;i < l;i++){
			if(a[i] < min) min = a[i];  ##  找出原字符串中字典循序最小的字符是
		}
		
		int start = 0;
		for(int i = 0;i < l;i++){
			if(a[i] == min){
				int k = i,s = 0;  ##  将当前耳朵下标记为k，s标记为0，遍历一次原字符串的长度
				for(int j = start;s < l;s++,j++,k++){
					if(j == l) j = 0;  ##  当达到l时，说明要返回下标0处继续遍历（圆环结构）
					if(k == l) k = 0;

					if(a[j] > a[k]){
						start = i;  ##  记录字典循序最小的串初始位置的下标
						break;
					}
					if(a[j] < a[k]) break;
				}
			}
		}
		for(int i = 0;i < l;i++,start++){
			if(start == l) start = 0;
			cout << a[start];
		}
		cout << endl;
	}
	return 0;
}

H-Puzzle （模拟题） UVA - 227

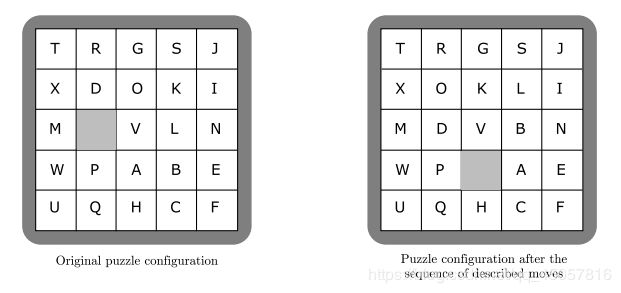
    A children’s puzzle that was popular 30 years ago consisted of a 5×5 frame which contained 24 small squares of equal size. A unique letter of the alphabet was printed on each small square. Since there were only 24 squares within the frame, the frame also contained an empty position which was the same size as a small square. A square could be moved into that empty position if it were immediately to the right, to the left, above, or below the empty position. The object of the puzzle was to slide squares into the empty position so that the frame displayed the letters in alphabetical order.
    The illustration below represents a puzzle in its original configuration and in its configuration after the following sequence of 6 moves:
        1) The square above the empty position moves.
        2) The square to the right of the empty position moves.
        3) The square to the right of the empty position moves.
        4) The square below the empty position moves.
        5) The square below the empty position moves.
        6) The square to the left of the empty position moves.

    Write a program to display resulting frames given their initial configurations and sequences of moves.

Input

    Input for your program consists of several puzzles. Each is described by its initial configuration and the sequence of moves on the puzzle. The first 5 lines of each puzzle description are the starting configuration. Subsequent lines give the sequence of moves.
    The first line of the frame display corresponds to the top line of squares in the puzzle. The other lines follow in order. The empty position in a frame is indicated by a blank. Each display line contains exactly 5 characters, beginning with the character on the leftmost square (or a blank if the leftmost square is actually the empty frame position). The display lines will correspond to a legitimate puzzle.
    The sequence of moves is represented by a sequence of As, Bs, Rs, and Ls to denote which square moves into the empty position. A denotes that the square above the empty position moves; B denotes that the square below the empty position moves; L denotes that the square to the left of the empty position moves; R denotes that the square to the right of the empty position moves. It is possible that there is an illegal move, even when it is represented by one of the 4 move characters. If an illegal move occurs, the puzzle is considered to have no final configuration. This sequence of moves may be spread over several lines, but it always ends in the digit 0. The end of data is denoted by the character Z.

Output

    Output for each puzzle begins with an appropriately labeled number (Puzzle #1, Puzzle #2, etc.). If the puzzle has no final configuration, then a message to that effect should follow. Otherwise that final configuration should be displayed.
    Format each line for a final configuration so that there is a single blank character between two adjacent letters. Treat the empty square the same as a letter. For example, if the blank is an interior position, then it will appear as a sequence of 3 blanks — one to separate it from the square to the left,one for the empty position itself, and one to separate it from the square to the right.
    Separate output from different puzzle records by one blank line.
Note: The first record of the sample input corresponds to the puzzle illustrated above.

Sample Input

TRGSJ
XDOKI
M VLN
WPABE
UQHCF
ARRBBL0
ABCDE
FGHIJ
KLMNO
PQRS
TUVWX
AAA
LLLL0
ABCDE
FGHIJ
KLMNO
PQRS
TUVWX
AAAAABBRRRLL0
Z

Sample Output

Puzzle #1:
T R G S J
X O K L I
M D V B N
W P A E
U Q H C F
Puzzle #2:
A B C D
F G H I E
K L M N J
P Q R S O
T U V W X
Puzzle #3:
This puzzle has no final configuration.

理解

	这道题要求你根据他过给出的操作进行一系列操作，得到一个新的图，但当他给出的操作不合法时，输出“This puzzle has no final configuration.”
	所以实际上你只要按照他的要求进行一个模拟即可，但存在两个难点。
	（1）你需要注意操作命令是否合法（即是否超出边界，此处可以参考wlacm P1016 奇数阶幻方，先读下一步的位置，在选择是否操作）。
	（2）输出格式，vj上面的模拟题对格式要求真的非常非常严格。（udebug是一个非常好的工具，在找格式错误这一方面）

AC代码

#include 
using namespace std;

int main()
{
	int q = 0;
	string m[6];
	while(getline(cin,m[0])){  ##  先输入第一行判断其首字符是否等于‘Z’，以判断是否结束程序
		if(m[0][0] == 'Z') break;
		for(int i = 1;i < 5;i++) getline(cin,m[i]);
		
		int l = 0;
		string k;  ##  k数组用于存入命令
		for(int i = 0;;i++){
			cin >> k[i];
			if(k[i] == '0'){
				l = i;
				break;
			}
		}
		getchar();  ##  不确定getline读不读回车，但无回车的情况下，后面样例受到影响
		
		int x = 0,y = 0,f = 0;
		for(int i = 0;i < 5;i++){  ##  二重循环寻找空格位
			for(int j = 0;j < 5;j++){
				if(m[i][j] == '\0') m[i][j] = ' ';  ##  getline行读入时会把行末空格换成'\0'，原因未知
				if(m[i][j] == ' '){
					x = i;
					y = j;
					break;
				}
			}
		}
		
		

		int x1 = x,y1 = y;
		for(int i = 0;i < l;i++){
			if(k[i] == 'A') x1 = x - 1;
			if(k[i] == 'R') y1 = y + 1;
			if(k[i] == 'B') x1 = x + 1;
			if(k[i] == 'L') y1 = y - 1;
			
			if(x1 < 0 || x1 > 4 || y1 < 0 || y1 > 4){
				f = 1;
				break;
			}
			
			swap(m[x][y],m[x1][y1]);
			x = x1;
			y = y1;
		}
		
		if(q) cout << endl;
		cout << "Puzzle #" << ++q << ":" << endl;
		if(f) cout << "This puzzle has no final configuration." << endl;
		
		else{
			for(int i = 0;i < 5;i++){  ## 这里本来使用的行输出，但行输出的数据会在getline读入的'\0'处输出'\0'，即便你已经改变了那个位置的字符
				for(int j = 0;j < 5;j++){
					if(j != 0) cout << ' ';
					cout << m[i][j];
				}
				cout << endl;
			}
		}
	}
	return 0;
}

I-Crossword Answers （模拟题） UVA - 232

    A crossword puzzle consists of a rectangular grid of black and white squares and two lists of definitions (or descriptions).
    One list of definitions is for “words” to be written left to right across white squares in the rows and the other list is for words to be written down white squares in the columns. (A word is a sequence of alphabetic characters.)
    To solve a crossword puzzle, one writes the words corresponding to the definitions on the white squares of the grid.
    The definitions correspond to the rectangular grid by means of sequential integers on “eligible” white squares.
White squares with black squares immediately to the left or above them are “eligible.” White squares with no squares either immediately to the left or above are also “eligible.” No other squares are numbered. All of the squares on the first row are numbered.The numbering starts with 1 and continues consecutively across white squares of the first row, then across the eligible white squares of the second row, then across the eligible white squares of the third row and so on across all of the rest of the rows of the puzzle. The picture below illustrates a rectangular crossword puzzle grid with appropriate numbering.
    An “across” word for a definition is written on a sequence of white squares in a row starting on a numbered square that does not follow another white square in the same row.
    The sequence of white squares for that word goes across the row of the numbered square, ending immediately before the next black square in the row or in the rightmost square of the row.
    A “down” word for a definition is written on a sequence of white squares in a column starting on a numbered square that does not follow another white square in the same column.
    The sequence of white squares for that word goes down the column of the numbered square, ending immediately before the next black square in the column or in the bottom square of the column.
    Every white square in a correctly solved puzzle contains a letter.
    You must write a program that takes several solved crossword puzzles as input and outputs the lists of across and down words which constitute the solutions.

Input

    Each puzzle solution in the input starts with a line containing two integers r and c (1 ≤ r ≤ 10 and 1 ≤ c ≤ 10), where r (the first number) is the number of rows in the puzzle and c (the second number) is the number of columns.
    The r rows of input which follow each contain c characters (excluding the end-of-line) which describe the solution. Each of those c characters is an alphabetic character which is part of a word or the character ‘*’, which indicates a black square.
    The end of input is indicated by a line consisting of the single number ‘0’.

Output

    Output for each puzzle consists of an identifier for the puzzle (puzzle #1:, puzzle #2:, etc.) and the list of across words followed by the list of down words. Words in each list must be output one-per-line in increasing order of the number of their corresponding definitions.
    The heading for the list of across words is ‘Across’. The heading for the list of down words is ‘Down’.
    In the case where the lists are empty (all squares in the grid are black), the ‘Across’ and ‘Down’ headings should still appear.
    Separate output for successive input puzzles by a blank line.

Sample Input

2 2
AT
O
6 7
AIMDEN
MEONE
UPONTO
SOERIN
SAOR*
IES*DEA
0

Sample Output

puzzle #1:
Across
1.AT
3.O
Down
1.A
2.TO
puzzle #2:
Across
1.AIM
4.DEN
7.ME
8.ONE
9.UPON
11.TO
12.SO
13.ERIN
15.SA
17.OR
18.IES
19.DEA
Down
1.A
2.IMPOSE
3.MEO
4.DO
5.ENTIRE
6.NEON
9.US
10.NE
14.ROD
16.AS
18.I
20.A

理解

	这道题的难度在于理解，在模拟实现上反而没那么难。
	可以把边界外的地方也视为*，方便理解题意。
	通过建立两个二维数组，一个用0和1标记这个位置是否为字母或是*（1为字母，0为*），第二个数组存该位置的标号（通过判断该位置上方或左方是否为0标号）。
	当该位置的左方为0时，就可以输出一个Across的单词。
	当该位置的上方为0时，就可以输出一个Down的单词。

AC代码

#include 
using namespace std;

int main()
{
	int a,b,s = 0;
	while(~scanf("%d",&a) && a){
		scanf("%d",&b);
		char m[11][11];
		int x[11][11] = {0},cnt = 1,y[11][11] = {0};  ##  x数组确认位置1或0，y数组用于存标号
		for(int i = 1;i <= a;i++) scanf("%s",m[i] + 1);
		
		for(int i = 1;i <= a;i++){  ##  一个二重循环预处理好x和y数组
			for(int j = 1;j <= b;j++){
				if(m[i][j] != '*') x[i][j] = 1;
				if(x[i][j] && (!x[i-1][j] || !x[i][j-1])) y[i][j] = cnt++;
			}
		}
		
		if(s) cout << endl;
		cout << "puzzle #" << ++s << ":" << endl << "Across" << endl;
		
		for(int i = 1;i <= a;i++){  ##  找Across的单词
			for(int j = 1;j <= b;j++){
				if(y[i][j] && !x[i][j - 1]){
					printf("%3d.",y[i][j]);
					for(int k = j;k <= b && x[i][k];k++){
						cout << m[i][k];
					}
					cout << endl;
				}
			}
		}
		
		cout << "Down" << endl;
		for(int i = 1;i <= a;i++){  ##  找Down的单词
			for(int j = 1;j <= b;j++){
				if(y[i][j] && !x[i - 1][j]){
					printf("%3d.",y[i][j]);
					for(int k = i;k <= a && x[k][j];k++){
						cout << m[k][j];
					}
					cout << endl;
				}
			}
		}
	}
	return 0;
}

J-Floating-Point Numbers （反向打表） UVA - 11809

    Floating-point numbers are represented differently in computers than integers. That is why a 32-bit floating-point number can represent values in the magnitude of 1038 while a 32-bit integer can only represent values as high as 232.
    Although there are variations in the ways floating-point numbers are stored in Computers, in this problem we will assume that floating-point numbers are stored in the following way:

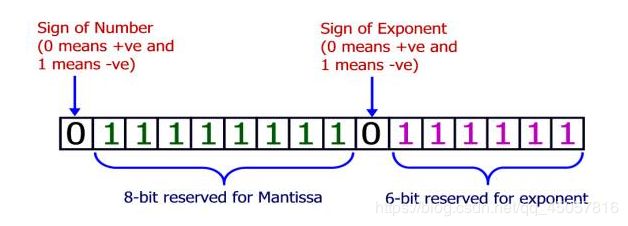
    Floating-point numbers have two parts mantissa and exponent. M-bits are allotted for mantissa and E bits are allotted for exponent. There is also one bit that denotes the sign of number (If this bit is 0 then the number is positive and if it is 1 then the number is negative) and another bit that denotes the sign of exponent (If this bit is 0 then exponent is positive otherwise negative). The value of mantissa and exponent together make the value of the floating-point number. If the value of mantissa is m then it maintains the constraints 1/2 ≤ m < 1. The left most digit of mantissa must always be 1 to maintain the constraint 1/2 ≤ m < 1. So this bit is not stored as it is always 1. So the bits in mantissa actually denote the digits at the right side of decimal point of a binary number (Excluding the digit just to the right of decimal point)
    In the figure above we can see a floating-point number where M = 8 and E = 6. The largest value this floating-point number can represent is (in binary) 0.1111111112 ×21111112.
    The decimal equivalent to this number is: 0.998046875 × 263 = 920535763834529382410. Given the maximum possible value represented by a certain floating point type, you will have to find how many bits are allotted for mantissa (M) and how many bits are allotted for exponent (E) in that certain type.

Input

    The input file contains around 300 line of input. Each line contains a floating-point number F that denotes the maximum value that can be represented by a certain floating-point type. The floating point number is expressed in decimal exponent format. So a number AeB actually denotes the value A×10B.
    A line containing ‘0e0’ terminates input. The value of A will satisfy the constraint 0 < A < 10 and will have exactly 15 digits after the decimal point.

Output

For each line of input produce one line of output. This line contains the value of M and E. You can assume that each of the inputs (except the last one) has a possible and unique solution. You can also assume that inputs will be such that the value of M and E will follow the constraints: 9 ≥ M ≥ 0 and 30 ≥ E ≥ 1. Also there is no need to assume that (M + E + 2) will be a multiple of 8.

Sample Input

5.699141892149156e76
9.205357638345294e18
0e0
Sample Output
5 8
8 6

理解

	这道题太狠了，简而言之，就是告诉了你浮点数是怎么来的，然后举了一个M=8，E=6的例子
	然后输入一个浮点数，要求是找出他的M是几位的，E是几位的，这里有个坑，通过M反算浮点数的时候要加一个1，例子里面就是M=8但有9个1，在这里
	卡了很久，自己做实验的时候数值老是对不上。
	看完网上的代码是打一个二维数组存A和B，B值实际上是有规律的整数，而且A值差别较大，就单独存了一个A（eps = 1-e4 时udebug会卡一个样例，
	而eps = 1-e5时能全过，也能在vj上ac）。
	
	数学公式
	A*10^B = (1 - 2^(-m-1)) * 2^(2^e - 1)
	设m1 = 1 - 2^(-m-1)
	  e1 = (2^e - 1)
	A*10^B = m1 * 2^e1
	两边取对数
	log10(A) + B = log10(m1) + 2*log10(e1)
	因为log10(A) < 1 所以 B = log10(m1) + 2*log10(e1) 向下取整
	最后可得A = 10^(log10(m1) + 2*log10(e1) - B)

AC代码

#include 
using namespace std;
const double pes = 1e-5;

int main()
{
	double m[11][32] = {0};
	double m1;
	int e1;
	for(int i = 0;i <= 9;i++){  ##  一个二维的数组，把所有A的数据存进去
		m1 = 1 - pow(2,-i-1);
		for(int j = 1;j <= 30;j++){
			e1 = pow(2,j) - 1;
			double x = log10(m1) + e1 * log10(2);
			int p = log10(m1) + e1 * log10(2);
			m[i][j] = pow(10,x - p);
//			printf("%d %d = %.6lf\n",i,j,m[i][j]);
		}
	}
	
	string s;
	while(cin >> s && s != "0e0"){  ##  找到e的位置，我们只要它之前的部分
		int l = s.size();
		int k = 0;
		for(int i = 0;i < l;i++){
			if(s[i] == 'e'){
				k = i;
				break;
			}
		}
		
		double a = 0;
		for(int i = 2;i < k;i++) a += (s[i] - '0') * pow(10,-i + 1);  ##  提取小数点之后的数字
		a += s[0] - '0';  ##  加上小数点前的数字
		
		int f = 0;
		for(int i = 0;i <= 9;i++){  ##  在表中查找A，找到了就退出查找
			for(int j = 1;j <= 30;j++){
				if(abs(a - m[i][j]) <= pes){
					cout << i << ' ' << j << endl;
					f = 1;
					break;
				}
			}
			if(f) break;
		}
	}
	return 0;
}

K-Fractions Again?! （典型暴力枚举） UVA - 10976

    It is easy to see that for every fraction in the form 1/k (k > 0), we can always find two positive integers x and y, x ≥ y, such that:

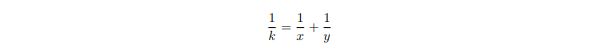
    Now our question is: can you write a program that counts how many such pairs of x and y there are for any given k?

Input

    Input contains no more than 100 lines, each giving a value of k (0 < k ≤ 10000).

Output

    For each k, output the number of corresponding (x, y) pairs, followed by a sorted list of the values of
x and y, as shown in the sample output.

Sample Input

2
12

Sample Output

2
1/2 = 1/6 + 1/3
1/2 = 1/4 + 1/4
8
1/12 = 1/156 + 1/13
1/12 = 1/84 + 1/14
1/12 = 1/60 + 1/15
1/12 = 1/48 + 1/16
1/12 = 1/36 + 1/18
1/12 = 1/30 + 1/20
1/12 = 1/28 + 1/21
1/12 = 1/24 + 1/24

理解

	其实这几道枚举算法的题目里面真的没啥难题，都能写，选这道是因为它数学成分多一点，以及枚举的范围稍微难找一点

	数学公式
	1/k = 1/x + 1/y
	变形得到 x = ky/(y - k)
	还因为 x >= y 所以 1/x <= 1/y
	代入数学公式可以得到 y <= 2k

AC代码

#include 
using namespace std;
int a[20005][2];

int main()
{
	int n;
	while(~scanf("%d",&n)){
		memset(a,0,sizeof(a));
		int cnt = 0;
		for(int i = n + 1;i <= n * 2;i++){  ##  y不可能小于等于k
			if((n*i) % (i - n) == 0){
				a[cnt][0] = (n*i)/(i - n);
				a[cnt++][1] = i;
			}
		}
		
		cout << cnt << endl;
		for(int i = 0;i < cnt;i++)
			printf("1/%d = 1/%d + 1/%d\n",n,a[i][0],a[i][1]);
	}
	return 0;
}

L-The Dole Queue （模拟题） UVA - 133

    In a serious attempt to downsize (reduce) the dole queue, The New National Green Labour Rhinoceros Party has decided on the following strategy. Every day all dole applicants will be placed in a large circle, facing inwards. Someone is arbitrarily chosen as number 1, and the rest are numbered counterclockwise up to N (who will be standing on 1’s left). Starting from 1 and moving counter-clockwise,one labour official counts off k applicants, while another official starts from N and moves clockwise,counting m applicants. The two who are chosen are then sent off for retraining; if both officials pick the same person she (he) is sent off to become a politician. Each official then starts counting again at the next available person and the process continues until no-one is left. Note that the two victims (sorry, trainees) leave the ring simultaneously, so it is possible for one official to count a person already selected by the other official.

Input

    Write a program that will successively read in (in that order) the three numbers (N, k and m; k, m > 0,0 < N < 20) and determine the order in which the applicants are sent off for retraining. Each set of three numbers will be on a separate line and the end of data will be signalled by three zeroes (0 0 0).

Output

    For each triplet, output a single line of numbers specifying the order in which people are chosen. Each number should be in a field of 3 characters. For pairs of numbers list the person chosen by the counterclockwise official first. Separate successive pairs (or singletons) by commas (but there should not be a trailing comma).
Note: The symbol ⊔ in the Sample Output below represents a space.

Sample Input

10 4 3
0 0 0

Sample Output

␣␣4␣␣8,␣␣9␣␣5,␣␣3␣␣1,␣␣2␣␣6,␣10,␣␣7

理解

	这道题本来是想去找网上的约瑟夫环递推公式理解一下，然后rush掉
	然后发现自己理解能力是真的不行，就想着写一个暴力模拟好了，k一定在m之前选人，然后判断是否是同一个人，以及找到下一个人的位置即可
	于是乎，代码写的真的非常暴力
	之后看到了大佬的代码，真的感叹模拟的方式，以及自定义函数的封装都十分重要，一个优秀的代码应该是自顶向下并且把重复操作归纳到一起的

AC代码

#include 
using namespace std;

int main()
{	
	int n,k,m,a[25];
	while(cin >> n >> k >> m && n && k && m){
		memset(a,0,sizeof(a));
		int s1 = 1,s2 = n,s = n;
		
		while(s){
			for(int i = 1;i < k;i++){  ##  k找人
				s1++;
				if(s1 > n) s1 = 1;
				if(a[s1]) i--;
			}
			for(int i = 1;i < m;i++){  ##  m找人
				s2--;
				if(s2 < 1) s2 = n;
				if(a[s2]) i--;
			}
			
			printf("%3d",s1);  ##  输出k找到的人
			a[s1] = !a[s1];
			s--;
			if(!a[s2]){  ##  判断m找到的人是否和k找到的人重复
				printf("%3d",s2);
				a[s2] = !a[s2];
				s--;
			}
			
			for(int i = 0;i < n;i++){  ##  找到k循序下下一个报数的人在哪
				s1++;
				if(s1 > n) s1 = 1;
				if(!a[s1]) break;
			}
			for(int i = 0;i < n;i++){  ##  找到m循序下下一个报数的人在哪
				s2--;
				if(s2 < 1) s2 = n;
				if(!a[s2]) break;
			}
			
			if(s) cout << ',';
			else cout << endl;
		}
	}
	return 0;
}

大佬的代码（非常优秀的大佬代码）

#include 
#include 
#include 
#include 
using namespace std;

int n, k, m;
int person[20];

int go(int s, int d, int p)
{
    while (d--) {
        do {
            s = (s+p+n) % n;
        } while (!person[s]);
    }
    return s;
}

int main(void)
{
    while (cin >> n >> k >> m, n || k || m) {
        memset(person, 1, sizeof(person));
        int left = n;
        int a = n-1, b = 0;
        while (left) {
            a = go(a, k, 1);
            b = go(b, m, -1);
            if (left < n) printf(",");
            printf("%3d", a+1);
            person[a] = 0;
            left --;
            if (person[b]) {
                printf("%3d", b+1);
                person[b] = 0;
                left --;
            }
            if (left == 0) break;
        }
        printf("\n");
    }

    return 0;
}
--------------------- 
作者：梁山伯liangrx06 
来源：CSDN 
原文：https://blog.csdn.net/thudaliangrx/article/details/50700688 
版权声明：本文为博主原创文章，转载请附上博文链接！

M-Message Decoding （巧妙打表题——外加巧妙的输入处理） UVA - 213

    Some message encoding schemes require that an encoded message be sent in two parts. The first part,called the header, contains the characters of the message. The second part contains a pattern that represents the message. You must write a program that can decode messages under such a scheme.
    The heart of the encoding scheme for your program is a sequence of “key” strings of 0’s and 1’s as follows:
                                0, 00, 01, 10, 000, 001, 010, 011, 100, 101, 110, 0000, 0001, . . . , 1011, 1110, 00000, . . .
    The first key in the sequence is of length 1, the next 3 are of length 2, the next 7 of length 3, the next 15 of length 4, etc. If two adjacent keys have the same length, the second can be obtained from the first by adding 1 (base 2). Notice that there are no keys in the sequence that consist only of 1’s.
    The keys are mapped to the characters in the header in order. That is, the first key (0) is mapped to the first character in the header, the second key (00) to the second character in the header, the kth key is mapped to the kth character in the header. For example, suppose the header is:

AB#TANCnrtXc

Then 0 is mapped to A, 00 to B, 01 to #, 10 to T, 000 to A, …, 110 to X, and 0000 to c.
    The encoded message contains only 0’s and 1’s and possibly carriage returns, which are to be ignored.
    The message is divided into segments. The first 3 digits of a segment give the binary representation of the length of the keys in the segment. For example, if the first 3 digits are 010, then the remainder of the segment consists of keys of length 2 (00, 01, or 10). The end of the segment is a string of 1’s which is the same length as the length of the keys in the segment. So a segment of keys of length 2 is terminated by 11. The entire encoded message is terminated by 000 (which would signify a segment in which the keys have length 0). The message is decoded by translating the keys in the segments one-at-a-time into the header characters to which they have been mapped.

Input

    The input file contains several data sets. Each data set consists of a header, which is on a single line by itself, and a message, which may extend over several lines. The length of the header is limited only by the fact that key strings have a maximum length of 7 (111 in binary). If there are multiple copies of a character in a header, then several keys will map to that character. The encoded message contains only 0’s and 1’s, and it is a legitimate encoding according to the described scheme. That is,the message segments begin with the 3-digit length sequence and end with the appropriate sequence of 1’s. The keys in any given segment are all of the same length, and they all correspond to characters in the header. The message is terminated by 000.
    Carriage returns may appear anywhere within the message part. They are not to be considered as part of the message.

Output

For each data set, your program must write its decoded message on a separate line. There should not be blank lines between messages.

Sample input

TNM AEIOU
0010101100011
1010001001110110011
11000
$#**
0100000101101100011100101000

Sample output

TAN ME
##*$

理解

	这道题真的是读题读到心态爆炸（英语水平太差了），后来在找了中文题意的情况下，我也没能读懂
	无奈，拉了别人的代码，看了别人代码输出的中间量，结合之前看的中文题意才读懂了这一题（苦笑）
	理解完之后写起来也就不难了，关键是怎么把二进制和字符串对照起来。
	
	可以发现二进制数之间的区别是长度，且不存在最大情况（及不存在1,11,111等情况）
	我们可以得出每个长度只有2^len - 1个数
	那么只要找到（0,00,000）等二进制对应的字符串数组的下标，再加上后面读入值的十进制，即可得到相应二进制对应的字符串数组下标

	得到递推公式
	a[1] = 0
	a[i] = a[i-1] + 2^(i-1)-1

AC代码

#include 
using namespace std;

void db(int a[]){  ##  打出0,00,000等对应的字符串数字下标，存到对应长度为下标的数组里
	int p = 2;
	a[1] = 0;
	for(int i = 2;i < 19;i++){
		a[i] = a[i - 1] + p - 1;
		p *= 2;
	}
}

int main()
{
	string s;
	int wz[20] = {0};
	db(wz);

	while(getline(cin,s)){
		int a,b,c;
		while(~scanf("%1d%1d%1d",&a,&b,&c) && (a || b || c)){  ##  输入标题的三个数，算出长度，并以此为长度读下面的数字
			int len = a*4+b*2+c;
			
			while(1){
				int sum = 0,js = 0;
				char v;
				for(int i = 0;i < len;i++){
					v = getchar();
					if(v == '1') js++;  ##  计数，当1的数量等于长度时，说明这个标题不再使用，退出循环
					if(v == '\n') i--;
					else sum = sum*2 + v - '0';
				}
			
				if(js == len) break;
				else cout << s[wz[len] + sum];
			}
		}
		getchar();
		cout << endl;
	}
	return 0;
}

N-IP Networks （模拟题） UVA - 1590

    Alex is administrator of IP networks. His clients have a bunch of individual IP addresses and he decided
to group all those IP addresses into the smallest possible IP network.
    Each IP address is a 4-byte number that is written byte-by-byte in a decimal dot-separated notation “byte0.byte1.byte2.byte3” (quotes are added for clarity). Each byte is written as a decimal number from 0 to 255 (inclusive) without extra leading zeroes.
    IP network is described by two 4-byte numbers — network address and network mask. Both network address and network mask are written in the same notation as IP addresses.
    In order to understand the meaning of network address and network mask you have to consider their binary representation. Binary representation of IP address, network address, and network mask consists of 32 bits: 8 bits for byte0 (most significant to least significant), followed by 8 bits for byte1,followed by 8 bits for byte2, and followed by 8 bits for byte3.
    IP network contains a range of 2n IP addresses where 0 ≤ n ≤ 32. Network mask always has 32 − n first bits set to one, and n last bits set to zero in its binary representation. Network address has arbitrary 32 − n first bits, and n last bits set to zero in its binary representation. IP network contains all IP addresses whose 32 − n first bits are equal to 32 − n first bits of network address with arbitrary n last bits. We say that one IP network is smaller than the other IP network if it contains fewer IP addresses.
    For example, IP network with network address 194.85.160.176 and network mask 255.255.255.248 contains 8 IP addresses from 194.85.160.176 to 194.85.160.183 (inclusive).

Input

    The input file will contain several test cases, each of them as described below.
    The first line of the input file contains a single integer number m (1 ≤ m ≤ 1000). The following m lines contain IP addresses, one address on a line. Each IP address may appear more than once in the input file.

Output

For each test case, write to the output file two lines that describe the smallest possible IP network that contains all IP addresses from the input file. Write network address on the first line and network mask on the second line.

Sample Input

3
194.85.160.177
194.85.160.183
194.85.160.178

Sample Output

194.85.160.176
255.255.255.248

理解

	大意：输入一堆ip地址，转换为二进制，找到他们的第一处不同点，保留前面相同点的情况下后面全改为0输出网络地址
														   相同点前全变成1，后面全为0的情况下输出网络掩
	所以只要暴力的模拟就行了

AC代码

#include 
using namespace std;

void stoi(int a[],string b){  ##  string to int 二进制字符串转十进制的ip地址和掩码
	int cnt = 0;
	for(int i = 0;i < 32;i += 8){
		int sum = 0;
		for(int j = i;j < i + 8;j++){
			sum = sum * 2 + b[j] - '0';
		}
		a[cnt++] = sum;
	}
}

int main()
{	
//	freopen("sample.in", "r", stdin);
//    freopen("sample.out", "w", stdout);
	
	int n;
	while(cin >> n){
		if(!n) continue;
		string s[n];
		int temp[4];
		for(int i = 0;i < n;i++){
			scanf("%d.%d.%d.%d",&temp[0],&temp[1],&temp[2],&temp[3]);  ##  输入ip并且直接转为字符串的二进制码
			int cnt = 0;
			string ss = "00000000000000000000000000000000";  ##　本来想写一个函数，但发现指针以及string类型使用不熟练，写错了，无奈改在主函数内
			for(int j = 7;j < 32;j += 8){
				int k = j;
				while(temp[cnt]){
					ss[k--] = temp[cnt] % 2 + '0';
					temp[cnt] /= 2;
				}
				cnt ++;
			}
			s[i] += ss;
		}
		
//		for(int i = 0;i < n;i++) cout << s[i] << endl;  ##  寻找第一个不同点
		int k;
		for(k = 0;k < 32;k++){
			int cnt = 0;
			for(int i = 0;i < n;i++){
				if(s[i][k] == '1') cnt++;
			}
			if(cnt > 0 && cnt < n) break;
		}
		
		string ans1 = "00000000000000000000000000000000";
		string ans2 = "11111111111111111111111111111111";
		for(int i = 0;i < k;i++) ans1[i] = s[0][i];  ##  生成ip地址二进制
		for(int i = k;i < 32;i++) ans2[i] = '0';  ##  生成ip掩码二进制
		
		int ans3[4],ans4[4];
		stoi(ans3,ans1);  ##  转成十进制
		stoi(ans4,ans2);
		
		printf("%d.%d.%d.%d\n",ans3[0],ans3[1],ans3[2],ans3[3]);
		printf("%d.%d.%d.%d\n",ans4[0],ans4[1],ans4[2],ans4[3]);
	}
	return 0;
}

O-Extraordinarily Tired Students （模拟题） UVA - 12108

    When a student is too tired, he can’t help sleeping in class, even if his favorite teacher is right here in front of him. Imagine you have a class of extraordinarily tired students, how long do you have to wait,before all the students are listening to you and won’t sleep any more? In order to complete this task,you need to understand how students behave.
    When a student is awaken, he struggles for a minutes listening to the teacher (after all, it’s too bad to sleep all the time). After that, he counts the number of awaken and sleeping students (including himself). If there are strictly more sleeping students than awaken students, he sleeps for b minutes.
    Otherwise, he struggles for another a minutes, because he knew that when there is only very few sleeping students, there is a big chance for them to be punished! Note that a student counts the number of sleeping students only when he wants to sleep again.
    Now that you understand each student could be described by two integers a and b, the length of awaken and sleeping period. If there are always more sleeping students, these two periods continue again and again. We combine an awaken period with a sleeping period after it, and call the combined period an awaken-sleeping period. For example, a student with a = 1 and b = 4 has an awaken-sleeping period of awaken-sleeping-sleeping-sleeping-sleeping. In this problem, we need another parameter c (1 ≤ c ≤ a + b) to describe a student’s initial condition: the initial position in his awaken-sleeping period.The 1st and 2nd position of the period discussed above are awaken and sleeping, respectively.
    Now we use a triple (a, b, c) to describe a student. Suppose there are three students (2, 4, 1), (1, 5,2) and (1, 4, 3), all the students will be awaken at time 18. The details are shown in the table below.

    Write a program to calculate the first time when all the students are not sleeping.

Input

    The input consists of several test cases. The first line of each case contains a single integer n (1 ≤ n ≤ 10), the number of students. This is followed by n lines, each describing a student. Each of these lines contains three integers a, b, c (1 ≤ a, b ≤ 5), described above. The last test case is followed by a single zero, which should not be processed.

Output

    For each test case, print the case number and the first time all the students are awaken. If it’ll never happen, output ‘-1’.

Sample Input

3
2 4 1
1 5 2
1 4 3
3
1 2 1
1 2 2
1 2 3
0

Sample Output

Case 1: 18
Case 2: -1

理解

	大意：一群人有一个醒的周期和一个睡的周期，当他在醒的周期的最后一秒，他会观察四周，如果周围睡觉的人比醒着的人多，他就“怒从心头
	起，恶向胆边生”，也睡觉去了，反之，他不敢睡觉，又会撑一个醒着的周期
	题目其实也是一个暴力模拟题，但它有和Repeating Decimals一样神奇的特质，如果所有人的状态回到和开头一样，即可视为一个循环，那么
	，也就可以得出他们是否会全醒过来了

AC代码

#include 
using namespace std;

struct student{
	int wake,sleep,zq;  ##  记录每个人的醒着，睡着，和当前状态的数值
} ss[10];
int sls = 0;

int iscf(int a[],int n){  ##  判断每个人的状态是否和开始时相同
	for(int i = 0;i < n;i++){
		if(a[i] != ss[i].zq) return 0;
	}
	return 1;
}

void issleep(int tsls,int n){  ##  判断这一秒时，所有人该会在下一秒做的选择
	for(int i = 0;i < n;i++){
		if(tsls > n - tsls){
			if(ss[i].zq == ss[i].wake) sls++;
			if(ss[i].zq == ss[i].sleep) sls--;
		}
		else{
			if(ss[i].zq == ss[i].wake) ss[i].zq = -1;
			if(ss[i].zq == ss[i].sleep) sls--;
		}
	}
}

int main()
{	
	int n,cnt2 = 0;
	while(cin >> n && n){
		int cnt = 1,x[10];
		sls = 0;
		for(int i = 0;i < n;i++){
			int a,b,c;
			scanf("%d %d %d",&a,&b,&c);
			ss[i].wake = a - 1;  ##  记录醒着的周期，减一是为了方便后面每个人的状态调整
			ss[i].sleep = a - 1 + b;  ##  睡眠时间加醒着时间形成一个完整周期，方便判断
			x[i] = ss[i].zq = c - 1;  ##  状态随之减一
			if(ss[i].zq > ss[i].wake) sls++;
		}
		
		int f = 0;
		while(1){
			if(sls == 0) break;  ##  刚开始如果都醒着就直接结束，此处先判断后操作是为了防止刚醒被认为是第二天全醒
			if(f){
				cnt = -1;
				break;
			}
			 
			if(cnt != 1 && iscf(x,n)) f = 1;  ##  除了第一轮判断，后面如果判断到状态全部相同，则说明不可能全醒，f标为1，触发开关
			cnt++;
			
			issleep(sls,n);
				
			for(int i = 0;i < n;i++) ss[i].zq = (ss[i].zq + 1) % (ss[i].sleep + 1);  ##  每个人的当前状态往前走一格
		}
		
		printf("Case %d: %d\n",++cnt2,cnt);
	}
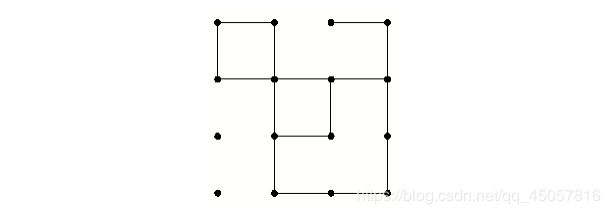
	return 0;
}

P-Squares （暴力枚举） UVA - 12108

    A children’s board game consists of a square array of dots that contains lines connecting some of the pairs of adjacent dots. One part of the game requires that the players count the number of squares of certain sizes that are formed by these lines. For example, in the figure shown below, there are 3 squares — 2 of size 1 and 1 of size 2. (The “size” of a square is the number of lines segments required to form a side.)

    Your problem is to write a program that automates the process of counting all the possible squares.

Input

    The input file represents a series of game boards. Each board consists of a description of a square array of n 2 dots (where 2 ≤ n ≤ 9) and some interconnecting horizontal and vertical lines. A record for a single board with n 2 dots and m interconnecting lines is formatted as follows:

Information for each line begins in column 1. The end of input is indicated by end-of-file. The first
record of the sample input below represents the board of the square above.

Output

    For each record, label the corresponding output with ‘Problem #1’, ‘Problem #2’, and so forth. Output for a record consists of the number of squares of each size on the board, from the smallest to the largest.
    lf no squares of any size exist, your program should print an appropriate message indicating so. Separate output for successive input records by a line of asterisks between two blank lines, like in the sample below.

Sample Input

4
16
H 1 1
H 1 3
H 2 1
H 2 2
H 2 3
H 3 2
H 4 2
H 4 3
V 1 1
V 2 1
V 2 2
V 2 3
V 3 2
V 4 1
V 4 2
V 4 3
2
3
H 1 1
H 2 1
V 2 1

Sample Output

Problem #1
2 square (s) of size 1
1 square (s) of size 2

---

Problem #2
No completed squares can be found.

理解

	我们可得得到第几行的第几天边是存在的，且这条边的长度必为1
	所以，我们想要确认大小为n的正方形是否存在，只要知道围着这个正方形的边是否都存在即可
	用2个二维数组存入行和列的边哪些是存在的，然后枚举即可

AC代码

#include 
using namespace std;
int a[10][10],b[10][10];

int Sq(int h,int v,int s){  ##  判断这个正方形的边是否都存在
	for(int i = 0;i < s;i++){
		if(!a[h][v + i]) return 0;
		if(!a[h + s][v + i]) return 0;
		if(!b[v][h + i]) return 0;
		if(!b[v + s][h + i]) return 0;
	}
	return 1;
}

void tj(int a[],int n){  ##  暴力枚举，ihej的组合可以成为网格中点的坐标，而k则是看这个大小的正方形是否存在，k会被i，j的位置限制
	for(int i = 1;i < n;i++){
		for(int j = 1;j < n;j++){
			for(int k = 1;k <= n - i && k <= n - j;k++){
				if(Sq(i,j,k)) a[k]++;
			}
		}
	}
}

int main()
{		
	int n,cnt = 0;
	while(cin >> n){
		memset(a,0,sizeof(a));
		memset(b,0,sizeof(b));
		
		int t,x,y;
		cin >> t;
		char c;
		for(int i = 0;i < t;i++){
			getchar();  ##  getchar会吃回车
			c = getchar();
			scanf("%d %d",&x,&y);
			
			if(c == 'H') a[x][y]++;
			else b[x][y]++;
		}
		
		int ans[10] = {0};  ##  打表，存每种大小的正方形有多少个
		tj(ans,n);	
		
		if(cnt) cout << endl << "**********************************" << endl << endl;
		printf("Problem #%d\n\n",++cnt);
		
		int f = 1;
		for(int i = 1;i < n;i++){
			if(ans[i]){
				printf("%d square (s) of size %d\n",ans[i],i);
				f = 0;
			}
		}
		if(f) printf("No completed squares can be found.\n");
	}
	return 0;
}

Q-Spreadsheet Tracking （模拟题） UVA - 512

    Data in spreadsheets are stored in cells, which are organized in rows ® and columns ©. Some operations on spreadsheets can be applied to single cells (r, c), while others can be applied to entire rows or columns. Typical cell operations include inserting and deleting rows or columns and exchanging cell contents.
    Some spreadsheets allow users to mark collections of rows or columns for deletion, so the entire collection can be deleted at once. Some (unusual) spreadsheets allow users to mark collections of rows or columns for insertions too. Issuing an insertion command results in new rows or columns being inserted before each of the marked rows or columns. Suppose, for example, the user marks rows 1 and 5 of the spreadsheet on the left for deletion. The spreadsheet then shrinks to the one on the right.

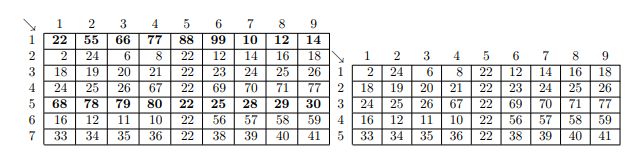
    If the user subsequently marks columns 3, 6, 7, and 9 for deletion, the spreadsheet shrinks to this.

    If the user marks rows 2, 3 and 5 for insertion, the spreadsheet grows to the one on the left. If the user then marks column 3 for insertion, the spreadsheet grows to the one in the middle. Finally, if the user exchanges the contents of cell (1,2) and cell (6,5), the spreadsheet looks like the one on the right.

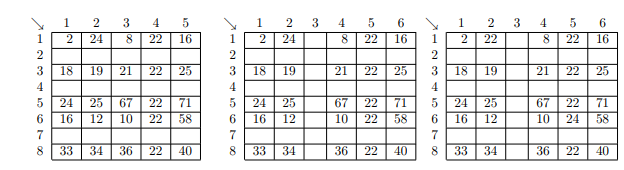
    You must write tracking software that determines the final location of data in spreadsheets that result from row, column, and exchange operations similar to the ones illustrated here.

Input

    The input consists of a sequence of spreadsheets, operations on those spreadsheets, and queries about them. Each spreadsheet definition begins with a pair of integers specifying its initial number of rows ® and columns ©, followed by an integer specifying the number (n) of spreadsheet operations. Row and column labeling begins with 1. The maximum number of rows or columns of each spreadsheet is limited to 50. The following n lines specify the desired operations.
    An operation to exchange the contents of cell (r1, c1) with the contents of cell (r2, c2) is given by:
EX r1 c1 r2 c2
    The four insert and delete commands—DC (delete columns), DR (delete rows), IC (insert columns),and IR (insert rows) are given by:
< command > A x1 x2 . . . xA
    where < command > is one of the four commands; A is a positive integer less than 10, and x1, . . . , xA are the labels of the columns or rows to be deleted or inserted before. For each insert and delete command, the order of the rows or columns in the command has no significance. Within a single delete or insert command, labels will be unique.
    The operations are followed by an integer which is the number of queries for the spreadsheet. Each query consists of positive integers r and c, representing the row and column number of a cell in the original spreadsheet. For each query, your program must determine the current location of the data that was originally in cell (r, c). The end of input is indicated by a row consisting of a pair of zeros for the spreadsheet dimensions.

Output

    For each spreadsheet, your program must output its sequence number (starting at 1). For each query,your program must output the original cell location followed by the final location of the data or the word ‘GONE’ if the contents of the original cell location were destroyed as a result of the operations.
    Separate output from different spreadsheets with a blank line.
    The data file will not contain a sequence of commands that will cause the spreadsheet to exceed the maximum size.

Sample Input

7 9
5
DR 2 1 5
DC 4 3 6 7 9
IC 1 3
IR 2 2 4
EX 1 2 6 5
4
4 8
5 5
7 8
6 5
0 0

Sample Output

Spreadsheet #1
Cell data in (4,8) moved to (4,6)
Cell data in (5,5) GONE
Cell data in (7,8) moved to (7,6)
Cell data in (6,5) moved to (1,2)

理解

	模拟题题型类似，一种是你按照他给你的指令逐步操作，一种按他题目的意思自己构架模拟方式。
	而前者则是这题，但这题如果按照他的指令来操作会显得十分复杂（蒟蒻真的模拟不来。。。暴风哭泣）
	所以这题的第二个思路就是把命令存起来，然后针对每个输入的位置依次执行命令（类似洛谷P1002 铺地毯，但那题贼简单，这题复杂不少）
	无论是删除还是添加，只有在输入位置的前面才会对其有影响

AC代码

#include 
using namespace std;

struct cmd{  ##  储存命令
	string ml;
	int a,b[11];
	int x1,y1,x2,y2;
} ss[100];

void IC(cmd *a,int n,int *c){  ##  执行添加列操作，下面四个类似
	int sum = 0;
	for(int i = 0;i < n;i++){
		if(a -> b[i] <= *c) sum++;
	}
	*c += sum;
	return;
}

void IR(cmd *a,int n,int *r){
	int sum = 0;
	for(int i = 0;i < n;i++){
		if(a -> b[i] <= *r) sum++;
	}
	*r += sum;
	return;
}

void EX(cmd *a,int *r,int *c){
	if(a -> x1 == *r && a -> y1 == *c){
		*r = a -> x2;
		*c = a -> y2;
	}
	else if(a -> x2 == *r && a -> y2 == *c){
		*r = a -> x1;
		*c = a -> y1;
	}
}

int DC(cmd *a,int n,int *c){
	int sum = 0;
	for(int i = 0;i < n;i++){
		if(a -> b[i] == *c) return 0;
		else if(a -> b[i] < *c) sum++;
	}
	*c -= sum;
	return 1;
}

int DR(cmd *a,int n,int *r){
	int sum = 0;
	for(int i = 0;i < n;i++){
		if(a -> b[i] == *r) return 0;
		else if(a -> b[i] < *r) sum++;
	}
	*r -= sum;
	return 1;
}

int main()
{	
	int m,n,cnt = 0;
	while(cin >> m >> n && m && n){
		int cmds;
		cin >> cmds;
		for(int i = 0;i < cmds;i++){  ##  存储命令
			cin >> ss[i].ml;
			if(ss[i].ml == "EX") cin >> ss[i].x1 >> ss[i].y1 >> ss[i].x2 >> ss[i].y2;
			else{
				cin >> ss[i].a;
				for(int j = 0;j < ss[i].a;j++) cin >> ss[i].b[j]; 
			}
		}
		
//		for(int i = 0;i < cmds;i++) cout << ss[i].ml << ' ' << ss[i].b[1] << endl;
//		cout << endl;

		if(cnt++) cout << endl;
		printf("Spreadsheet #%d\n",cnt);
		
		int cx;
		cin >> cx;
		for(int i = 0;i < cx;i++){
			int r,c,f = 1;
			cin >> r >> c;
			printf("Cell data in (%d,%d)",r,c);
			for(int j = 0;j < cmds;j++){
				if(ss[j].ml == "EX") EX(&ss[j],&r,&c);
				if(ss[j].ml == "IC") IC(&ss[j],ss[j].a,&c);
				if(ss[j].ml == "IR") IR(&ss[j],ss[j].a,&r);
				if(ss[j].ml == "DC"){
					if(!DC(&ss[j],ss[j].a,&c)){
						f = 0;
						break;
					}
				}
				if(ss[j].ml == "DR"){
					if(!DR(&ss[j],ss[j].a,&r)){
						f = 0;
						break;
					}
				}
			}
			if(!f) printf(" GONE\n");
			else printf(" moved to (%d,%d)\n",r,c);
		} 
	} 
	return 0;
}

R-计算器的改良 （模拟题 + 字符串处理） 洛谷P1022

题目背景
    NCLNCL是一家专门从事计算器改良与升级的实验室，最近该实验室收到了某公司所委托的一个任务：需要在该公司某型号的计算器上加上解一元一次方程的功能。实验室将这个任务交给了一个刚进入的新手ZL先生。

题目描述
    为了很好的完成这个任务，ZLZL先生首先研究了一些一元一次方程的实例：

    4+3x=84+3x=8

    6a-5+1=2-2a6a−5+1=2−2a

    -5+12y=0−5+12y=0

    ZLZL先生被主管告之，在计算器上键入的一个一元一次方程中，只包含整数、小写字母及+、-、=这三个数学符号（当然，符号“-”既可作减号，也可作负号）。方程中并没有括号，也没有除号，方程中的字母表示未知数。

    你可假设对键入的方程的正确性的判断是由另一个程序员在做，或者说可认为键入的一元一次方程均为合法的，且有唯一实数解。

Input

一个一元一次方程。

Output

解方程的结果(精确至小数点后三位)。

Sample Input

6a-5+1=2-2a

Sample Output

a=0.750

理解

	唯一做的一道“普及/提高-”的题，没有想的那么难
	为了处理一元一次方程，模拟手算的方式，将带字母的存在左边，将不带字母的存在右边
	代码并不巧妙，重复处理较明显，后面有时间会考虑改进代码

AC代码

#include 
using namespace std;

int main()
{
	char x;
	double left = 0,right = 0;  ##  left记录未知数的系数，right记录已知值
	string s;
	cin >> s;
	int l = s.size(),i = 0;
	
	int k = 0;
	for(int j = 0;j < l;j++){
		if(s[j] == '='){
			k = j;
			break;
		}
	}
	for(int j = 0;j < l;j++){
		if(s[j] >= 'a' && s[j] <= 'z'){
			x = s[j];
			break;
		}
	}
	
	if(s[0] == '-'){
		int sum = 0;
		for(i = 1;s[i] >= '0' && s[i] <= '9' && i < k;i++){
			sum = sum * 10 + s[i] - '0';
		}
		if(s[i] >= 'a' && s[i] <= 'z'){
			if(sum == 0) sum++;
			left -= sum;
			i++;
		}
		else right += sum;
	}
	else{
		int sum = 0;
		for(i = 0;s[i] >= '0' && s[i] <= '9' && i < k;i++){
			sum = sum * 10 + s[i] - '0';
		}
		if(s[i] >= 'a' && s[i] <= 'z'){
			if(sum == 0) sum++;
			left += sum;
			i++;
		}
		else right -= sum;
	}
	
	for(;i < k;i++){
		if(s[i] == '-' || s[i] == '+'){
			int sum = 0,j;
			for(j = i + 1;j < k && s[j] >= '0' && s[j] <= '9';j++){
				sum = sum * 10 + s[j] - '0';
			}
			if(s[j] >= 'a' && s[j] <= 'z'){
				if(sum == 0) sum++;
				if(s[i] == '-') left -= sum;
				else left += sum;
			}
			else{
				if(s[i] == '-') right += sum;
				else right -= sum;
			}
		}
	}
	i++;
	
	if(s[i] == '-'){
		i++;
		int sum = 0;
		for(;s[i] >= '0' && s[i] <= '9' && i < l;i++){
			sum = sum * 10 + s[i] - '0';
		}
		if(s[i] >= 'a' && s[i] <= 'z'){
			if(sum == 0) sum++;
			left += sum;
			i++;
		}
		else right -= sum;
	}
	else{
		int sum = 0;
		for(;s[i] >= '0' && s[i] <= '9' && i < l;i++){
			sum = sum * 10 + s[i] - '0';
		}
		if(s[i] >= 'a' && s[i] <= 'z'){
			if(sum == 0) sum++;
			left -= sum;
			i++;
		}
		else right += sum;
	}
	
	for(;i < l;i++){
		if(s[i] == '-' || s[i] == '+'){
			int sum = 0,j;
			for(j = i + 1;j < l && s[j] >= '0' && s[j] <= '9';j++){
				sum = sum * 10 + s[j] - '0';
			}
			if(s[j] >= 'a' && s[j] <= 'z'){
				if(sum == 0) sum++;
				if(s[i] == '-') left += sum;
				else left -= sum;
			}
			else{
				if(s[i] == '-') right -= sum;
				else right += sum;
			}
		}
	}
	
	if(right == 0) printf("%c=0.000",x);
	else printf("%c=%.3f",x,right/left);
	return 0;
}

（二）一些收获

1.关于取模运算

	基本性质
	若p|(a-b)，则a≡b (% p)。例如 11 ≡ 4 (% 7)， 18 ≡ 4(% 7)
	(a % p)=(b % p)意味a≡b (% p)
	对称性：a≡b (% p)等价于b≡a (% p)
	传递性：若a≡b (% p)且b≡c (% p) ，则a≡c (% p)
	
	运算规则
	模运算与基本四则运算有些相似，但是除法例外。其规则如下：
	(a + b) % p = (a % p + b % p) % p 
	(a - b) % p = (a % p - b % p) % p 
	(a * b) % p = (a % p * b % p) % p 
	a ^ b % p = ((a % p)^b) % p 
	
	结合律：
	((a+b) % p + c) % p = (a + (b+c) % p) % p 
	((a*b) % p * c)% p = (a * (b*c) % p) % p 
	
	交换律：
	(a + b) % p = (b+a) % p 
	(a * b) % p = (b * a) % p 
	
	分配律：
	(a+b) % p = ( a % p + b % p ) % p 
	((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p 
	
	重要定理
	若a≡b (% p)，则对于任意的c，都有(a + c) ≡ (b + c) (%p)
	若a≡b (% p)，则对于任意的c，都有(a * c) ≡ (b * c) (%p)
	若a≡b (% p)，c≡d (% p)，则 (a + c) ≡ (b + d) (%p)，(a - c) ≡ (b - d) (%p)，(a * c) ≡ (b * d) (%p)； 

论实际掌握而言并没有很深的理解，目前对其的运用停留在对运算规则的掌握，还需加强！！！（特别是重要定理那一块）

2.关于打表

1.实际上，个人理解的打表的作用分为三种：
（1）保存数据，方便直接进行查找，以减少重复运算，解决tle的问题（如：Digit Generator此题，大量的枚举极有可能超时，但打表之后可以大大减少
	 枚举次数）。
（2）根据题意，通过打表的方式预处理一些必要的内容，方便后面进行查找（如：Message Decoding此题，刚开始我用了二维数组打表预处理输入的字符
	 串，后改为一维输出存“0”，“00“等值的下标，都是一种通过打表对数组进行预处理的方式）。
（3）通过打一个bool或者int的数组，用于标记状态或者计数，也是我们最长用的打表方式，一般用于模拟状态或者统计字符出现次数。

2.关于打表的思路
	针对第一种打表：
		（1）最常见的思路是通过输入打表预存输出，然后通过输入直接输出表中数据，一般用于解决重复计算的问题，算比较笨但非常实用的方式。
		（2）反向思路，最典型的就是目前遇到的“Digit Generator”，根据结果找输入的表，一般当（1）情况下暴力枚举可能超时的情况下进行反向打
			 表以上两种打表本质目的是减小枚举次数，具体怎么打表还是得看题目而言，选择打出的表应当能使“查找数据的枚举次数”加上“打表时的枚
			 举次数”尽可能少。
	
	针对第二种打表：
		这种预处理的打表只能看个人对题目的理解，选择比较巧妙的方式进行打表最好，目前就“Message Decoding”完成了从二维数组存字母到一维数
		组存下标的改进，而“Squares”这题没想到什么优秀写法，就只能用行和列的两个二维数组对数据进行了预处理。
		具体做题时应当选择优先选择较为巧妙的预处理方式，如果第一时间构思不出巧妙的预处理方式，就进行简单的模拟存储，用笨办法先写题，方法
		的优化是具有一定共同性的，写的过程中可能会得到更好的预处理方式（纯粹自己扯淡，目前只在事后实现过优化）。

	针对第三种打表：
		emm 一般用于模拟题比较多，看情况灵活使用吧，只能说熟能生巧，告辞。

3.关于打表的衍生：
（1）记忆化搜索，将打表和搜索结合，以完成搜索的剪枝（洛谷P1464 Function 、PAT (Basic Level) Practice （中文）1005 继续(3n+1)猜想）
（剩下待补充，暂时没新东西）

3.关于枚举算法

	实际上枚举算法是我们用的最多也最基础的算法了，大概注意一下下面两点
	（1）注意枚举范围，一个好的枚举算法应该充分考虑枚举的有效范围，防止无效的空转（避免tle），而范围一般由题意给出，所以尽可能捕捉题中的
		 信息。
	（2）注意枚举过程中判断条件的选择，这个跟题意来了，重点还是看理解。
	（如果还有会继续补充）

4.关于贪心

	现在做的题里面也已经有不少贪心的题型了，线性的能写写，上升到dp目前还是等死状态。
	关键在于建立当前情况下的最优解，且这个解法能适用于接下来的一系列情况，通过每次的最优解得到正确结果。
	不过一般都直接上dp了，线性贪心难度也没那么高，一般只会从题意理解处为难一些可乐的选手。
	（理解不深，会随理解继续补充，目前也没看到特别好的线性贪心题，ants不太行）

5.关于模拟题

	简单的模拟题也是不少，有那么一点点想法
	（1）模拟题细节众多，你很难从头写到尾并且一次写对（有些题我用udebug测了许久的样例，一次写对的emm 确实太少了），写模拟题应该先写框架
		 及确定大框架后逐步完善细节（可能类似自顶向下，但个人理解过来就是一种“分治思想”，拆分问题，逐步解决）。所谓的大框架，目前个人而
		 言，及时确定输入，输出的框架，以及其中该有模块的位置先预留好。
	（2）模拟的方法十分重要，好的模拟应该把大量重复的操作的共性找出来，以缩减代码量，印象最深的即是Othello UVA - 220，因为缺乏巧妙的方式
		 我进行的暴力模拟写了整整362行代码，虽然能过udebug的样例测试，但还是倒在了vj上，而大佬的代码则十分简短且巧妙。

（三）个人感受

1.关于写题

    第一周被题目折磨过来也算有一点收获
    1.对于打表，枚举，函数之类的有了更深的理解，就是运用的更熟练了，后面几天的题目有涉及的打表的，也能挺容易想到打表这个方法
    2.对于解决问题有了更深的理解，对于以前的简单题而言，写代码是很随意的时候，因为代码行数极少，写起来也很容易，对分治思想没
       啥感受,就现在而言，因为题目难度上去了，更多是时候，习惯性分成一小块一小块来写，对问题的拆分有了联系（虽然只是在主函数里
       对不同作用的代码进行分隔）。之后需要努力的方向是将其外置，写成自定义函数封装，把分而治之做的更好点，代码写起来也更有条
       理（主要是指针这一块不熟，对于数据的传导啥的总感觉用不惯，有不敢随便用全局变量。。。暴风哭泣）。

2.关于学习新内容

    说实话，第一周在新知识点的学习上快接近0了，数据结构视频观影进度推进为0，STL学习进度推进一点点（就看了一点队列的内容），C++新内容的学习推进进度也贼缓慢（就懂了点输入输出，学了个string，连string包含的函数都没有学几个）。因为大部分时间都被那来自闭写题，所以新知识点的学习上就比较尴尬了。
    打算从下周开始对写题和学新内容的时间做一个平衡，没有新内容支撑，写一些难度上去的题目是很无力的，就像洛谷一道线性贪心的题（P1090 合并果子），用优先队列就可以很快解决，而用老的知识，则要排序不知道多少次，一道简单题却写的很繁琐。

（四）一些附录

1.cin（基础内容）

（1）cin的读入方式
       1.当我们从键盘输入字符串的时候需要敲一下回车键才能够将这个字符串送入到缓冲区中，那么敲入的这个回车键(\r)会被转换为一个换行符\n，这个换行符\n也会被存储在cin的缓冲区中并且被当成一个字符来计算！比如我们在键盘上敲下了123456这个字符串，然后敲一下回车键（\r）将这个字符串送入了缓冲区中，那么此时缓冲区中的字节个数是7 ，而不是6。
        cin读取数据也是从缓冲区中获取数据，缓冲区为空时，cin的成员函数会阻塞等待数据的到来，一旦缓冲区中有数据，就触发cin的成员函数去读取数据。
       2.当cin>>从缓冲区中读取数据时，若缓冲区中第一个字符是空格、tab或换行这些分隔符时，cin>>会将其忽略并清除，继续读取下一个字符，若缓冲区为空，则继续等待。但是如果读取成功，字符后面的分隔符是残留在缓冲区的，cin>>不做处理。
       3.不想略过空白字符，那就使用 noskipws 流控制。比如cin>>noskipws>>input;

2.cin.get

（1）cin.get的读入方式
       1.cin.get()从输入缓冲区读取单个字符时不忽略分隔符，直接将其读取（类似getchar()）。
       2.get ( char* s, streamsize n )读取一行时，遇到换行符时结束读取，但是不对换行符进行处理，换行符仍然残留在输入缓冲区。

3.cin.getline

（1）cin.getline的读入方式
       1.cin.getline与cin.get的区别是，cin.getline不会将结束符或者换行符残留在输入缓冲区中。

摘自 https://blog.csdn.net/bravedence/article/details/77282039 会随学习进度前进继续增添内容

4.string（基础内容）

string str：生成空字符串
string s(str)：生成字符串为str的复制品
string s(str, strbegin,strlen)：将字符串str中从下标strbegin开始、长度为strlen的部分作为字符串初值
string s(cstr, char_len)：以C_string类型cstr的前char_len个字符串作为字符串s的初值
string s(num ,c)：生成num个c字符的字符串
string s(str, stridx)：将字符串str中从下标stridx开始到字符串结束的位置作为字符串初值

str1.size()和str1.length()：返回string对象的字符个数，他们执行效果相同。
str1.max_size()：返回string对象最多包含的字符数，超出会抛出length_error异常
str1.capacity()：重新分配内存之前，string对象能包含的最大字符数
str1.compare(index1,len1,str2,index2,len2)：支持用索引值和长度定位子串来进行比较。(str2必备)
str1.push_back()：尾部插入
str1.insert(index,char s)：指定位置插入
str1.erase(index1,index2)：指定删除（只输入一个时删除单个字符）
str1.begin() == str1[0];
str1.end() == str1[str1.size - 1];
str1.replace(size_t pos, size_t n, const char *s)：将当前字符串
str1.replace(size_t pos, size_t n, size_t n1, char c)：将当前字符串从pos索引开始的n个字符，替换成n1个字符c
str1.replace(iterator i1, iterator i2, const char* s)：将当前字符串[i1,i2)区间中的字符串替换为字符串s
str1.substr(index1,len)：截取长度

string s("dog bird chicken bird cat");
//字符串查找-----找到后返回首字母在字符串中的下标
// 1. 查找一个字符串
cout << s.find("chicken") << endl;        // 结果是：9
// 2. 从下标为6开始找字符'i'，返回找到的第一个i的下标
cout << s.find('i',6) << endl;            // 结果是：11
// 3. 从字符串的末尾开始查找字符串，返回的还是首字母在字符串中的下标
cout << s.rfind("chicken") << endl;       // 结果是：9
// 4. 从字符串的末尾开始查找字符
cout << s.rfind('i') << endl;             // 结果是：18-------因为是从末尾开始查找，所以返回第一次找到的字符
// 5. 在该字符串中查找第一个属于字符串s的字符
cout << s.find_first_of("13br98") << endl;  // 结果是：4---b
// 6. 在该字符串中查找第一个不属于字符串s的字符------先匹配dog，然后bird匹配不到，所以打印4
cout << s.find_first_not_of("hello dog 2006") << endl; // 结果是：4
cout << s.find_first_not_of("dog bird 2006") << endl;  // 结果是：9
// 7. 在该字符串最后中查找第一个属于字符串s的字符
cout << s.find_last_of("13r98") << endl;               // 结果是：19
// 8. 在该字符串最后中查找第一个不属于字符串s的字符------先匹配t--a---c，然后空格匹配不到，所以打印21
cout << s.find_last_not_of("teac") << endl;            // 结果是：21

sort(s.begin(),s.end()):排序

摘自 https://blog.csdn.net/qq_37941471/article/details/82107077 会随学习进度前进继续增添内容

5.未能ac的题 —— Othello UVA - 220

	花了4个半小时写的暴力模拟代码，侥幸udebug全过，但死在vj，虽然wa，但写题写完之后，对构架的感觉清晰了几分，所以保存一份代码，纪念一下
	最好之后能改好，成功补题

#include 
using namespace std;
char m[9][9];
int wsum,bsum;

void Q(){
	for(int i = 1;i <= 8;i++){
		for(int j = 1;j <= 8;j++){
			printf("%c",m[i][j]);
		}
		printf("\n");
	}
}

int M(int x,int y,char k){
//	cout << "k = " << k << endl;
	m[x][y] = k;
	char k2 = (k == 'W') ?'B' :'W';
	int sum = 0,start = 0,f = 1;
	for(int i = 1;i < x;i++){
		if(m[i][y] == k) start = i;
	}
	if(start){
		for(int i = start + 1;i < x;i++){
			if(m[i][y] != k2){
				f = 0;
				break;
			}
		}
		if(f){
			for(int i = start + 1;i < x;i++){
				if(m[i][y] == k2){m[i][y] = k;sum++;}
			}
		}
	}
	
	start = 9,f = 1;
	for(int i = 8;i > x;i--){
		if(m[i][y] == k) start = i;
	}
	if(start != 9){
		for(int i = start - 1;i > x;i--){
			if(m[i][y] != k2){
				f = 0;
				break;
			}
		}
		if(f){
			for(int i = start - 1;i > x;i--){
				if(m[i][y] == k2){m[i][y] = k;sum++;}
			}
		}
	}
	
	start = 9,f = 1;
	for(int i = 8;i > y;i--){
		if(m[x][i] == k) start = i;
	}
	if(start != 9){
		for(int i = start - 1;i > y;i--){
			if(m[x][i] != k2){
				f = 0;
				break;
			}
		}
		if(f){
			for(int i = start - 1;i > y;i--){
				if(m[x][i] == k2){m[x][i] = k;sum++;}
			}
		}
	}
	
	start = 0,f = 1;
	for(int i = 0;i < y;i++){
		if(m[x][i] == k) start = i;
	}
	if(start){
		for(int i = start + 1;i < y;i++){
			if(m[x][i] != k2){
				f = 0;
				break;
			}
		}
		if(f){
			for(int i = start + 1;i < y;i++){
				if(m[x][i] == k2){m[x][i] = k;sum++;}
			}
		}
	}
	
	int x1 = x + 1,y1 = y + 1;
	f = 1;
	while(x1 < 9 && y1 < 9){
		if(m[x1][y1] == k) break;
		x1++;
		y1++;
	}
	if(x != x1 && y != y1){
		for(int i = x1 - 1,j = y1 - 1;i > x && j > y;i--,j--){
			if(m[i][j] != k2){
				f = 0;
				break;
			}
		}
		if(f){
			for(int i = x1 - 1,j = y1 - 1;i > x && j > y;i--,j--)
			if(m[i][j] == k2){m[i][j] = k;sum++;}
		}
	}
	
	x1 = x + 1,y1 = y - 1,f = 1;
	while(x1 < 9 && y1 > 0){
		if(m[x1][y1] == k) break;
		x1++;
		y1--;
	}
	if(x != x1 && y != y1){
		for(int i = x1 - 1,j = y1 + 1;i > x && j < y;i--,j++){
			if(m[i][j] != k2){
				f = 0;
				break;
			}
		}
		if(f){
			for(int i = x1 - 1,j = y1 + 1;i > x && j < y;i--,j++)
			if(m[i][j] == k2){m[i][j] = k;sum++;}
		}
	}
	
	x1 = x - 1,y1 = y - 1,f = 1;
	while(x1 > 0 && y1 > 0){
		if(m[x1][y1] == k) break;
		x1--;
		y1--;
	}
	if(x != x1 && y != y1){
		for(int i = x1 + 1,j = y1 + 1;i < x && j < y;i++,j++){
			if(m[i][j] != k2){
				f = 0;
				break;
			}
		}
		if(f){
			for(int i = x1 + 1,j = y1 + 1;i < x && j < y;i++,j++)
			if(m[i][j] == k2){m[i][j] = k;sum++;}
		}
	}
	
	x1 = x - 1,y1 = y + 1,f = 1;
	while(x1 > 0 && y1 < 9){
		if(m[x1][y1] == k) break;
		x1--;
		y1++;
	}
	if(x != x1 && y != y1){
		for(int i = x1 + 1,j = y1 - 1;i < x && j > y;i++,j--){
			if(m[i][j] != k2){
				f = 0;
				break;
			}
		}
		if(f){
			for(int i = x1 + 1,j = y1 - 1;i < x && j > y;i++,j--)
			if(m[i][j] == k2){m[i][j] = k;sum++;}
		}
	}
	
	if(k == 'W'){wsum += sum;bsum -= sum;}
	else{bsum += sum;wsum -= sum;}
	if(k == 'W' && sum) wsum++;
	if(k == 'B' && sum) bsum++;
	return sum;
}

int L(char k){
//	cout << "k" << " = " << k << endl;
	char k2 = (k == 'W') ?'B' :'W';
	int f = 0;
	for(int i = 1;i <= 8;i++){
		for(int j = 1;j <= 8;j++){
			if(m[i][j] == '-'){
				int f2 = 0,f3 = 0;
				for(int x = i - 1;x > 0;x--){
					if(m[x][j] == k2) f2 = 1;
					if(m[x][j] == k && f2){
						f3 = 1;
						break;
					}
					if(m[x][j] != k2) break;
				}
				if(f3){
					if(f) printf(" ");
					printf("(%d,%d)",i,j);
					f = 1;
					continue;
				}
				
				f2 = 0,f3 = 0;
				for(int x = i + 1;x < 9;x++){
					if(m[x][j] == k2) f2 = 1;
					if(m[x][j] == k && f2){
						f3 = 1;
						break;
					}
					if(m[x][j] != k2) break;
				}
				if(f3){
					if(f) printf(" ");
					printf("(%d,%d)",i,j);
					f = 1;
					continue;
				}
				
				f2 = 0,f3 = 0;
				for(int y = j + 1;y < 9;y++){
					if(m[i][y] == k2) f2 = 1;
					if(m[i][y] == k && f2){
						f3 = 1;
						break;
					}
					if(m[i][y] != k2) break;
				}
				if(f3){
					if(f) printf(" ");
					printf("(%d,%d)",i,j);
					f = 1;
					continue;
				}
				
				f2 = 0,f3 = 0;
				for(int y = j - 1;y > 0;y--){
					if(m[i][y] == k2) f2 = 1;
					if(m[i][y] == k && f2){
						f3 = 1;
						break;
					}
					if(m[i][y] != k2) break;
				}
				if(f3){
					if(f) printf(" ");
					printf("(%d,%d)",i,j);
					f = 1;
					continue;
				}
				
				f2 = 0,f3 = 0;
				for(int x = i + 1,y = j + 1;x < 9 && y < 9;x++,y++){
					if(m[x][y] == k2) f2 = 1;
					if(m[x][y] == k && f2){
						f3 = 1;
						break;
					}
					if(m[x][y] != k2) break;
				}
				if(f3){
					if(f) printf(" ");
					printf("(%d,%d)",i,j);
					f = 1;
					continue;
				}
				
				f2 = 0,f3 = 0;
				for(int x = i + 1,y = j - 1;x < 9 && y > 0;x++,y--){
					if(m[x][y] == k2) f2 = 1;
					if(m[x][y] == k && f2){
						f3 = 1;
						break;
					}
					if(m[x][y] != k2) break;
				}
				if(f3){
					if(f) printf(" ");
					printf("(%d,%d)",i,j);
					f = 1;
					continue;
				}
				
				f2 = 0,f3 = 0;
				for(int x = i - 1,y = j - 1;x > 0 && y > 0;x--,y--){
					if(m[x][y] == k2) f2 = 1;
					if(m[x][y] == k && f2){
						f3 = 1;
						break;
					}
					if(m[x][y] != k2) break;
				}
				if(f3){
					if(f) printf(" ");
					printf("(%d,%d)",i,j);
					f = 1;
					continue;
				}
				
				f2 = 0,f3 = 0;
				for(int x = i - 1,y = j + 1;x > 0 && y < 9;x--,y++){
					if(m[x][y] == k2) f2 = 1;
					if(m[x][y] == k && f2){
						f3 = 1;
						break;
					}
					if(m[x][y] != k2) break;
				}
				if(f3){
					if(f) printf(" ");
					printf("(%d,%d)",i,j);
					f = 1;
					continue;
				}
			}
		}
	}
	return f;
}

int main()
{
//	freopen("sample.in","r",stdin);
//	freopen("sample.out","w",stdout);
	
	int t;
	cin >> t;
	while(t--){
		wsum = 0;
		bsum = 0;
		getchar();
		for(int i = 1;i <= 8;i++) fgets(m[i] + 1,20,stdin);
		for(int i = 1;i <= 8;i++){
			for(int j = 1;j <= 8;j++){
				if(m[i][j] == 'B') bsum++;
				if(m[i][j] == 'W') wsum++;
			}
		}
		
		char cqr;
		cqr = getchar();
		
		while(1){
			string cmd;
			cin >> cmd;
			
			if(cmd[0] == 'Q'){Q();break;}
			if(cmd[0] == 'M'){
				int f = 0;
				int x = cmd[1] - '0',y = cmd[2] - '0';
				if(M(x,y,cqr)) f = 1;
				if(!f){
					cqr = (cqr == 'W') ?'B' :'W';
					M(x,y,cqr);
				}
				printf("Black - %2d White - %2d\n",bsum,wsum);
				cqr = (cqr == 'W') ?'B' :'W';
//				Q();
			}
			if(cmd[0] == 'L'){
				if(L(cqr)) printf("\n");
				else printf("No legal move.\n");
			}
		}
		if(t) cout << endl;
	}
	return 0;
}